法布里-珀罗谐振腔中石墨烯的等离激元光学性质

秦俊飞， 杨国晖，赵承祥,2*， 高卓瑶，李畅， 赵诗杰， 王添钰

1.山西师范大学物理与信息工程学院，山西 临汾 041000；2.山西师范大学现代文理学院，山西 临汾 041000

0 引言

金属表面等离激元是由金属和介质界面处电子的集体振荡产生的电磁模式, 这种模式表现出特殊的光学性质[1～3],如局域效应、近场增强、波长相对于自由空间的电磁波缩短等.当用入射光激发这种电磁模式时，光被金属表面等离激元所捕获并转化为表面等离极化激元这种耦合模式的能量，并且限制在金属表面沿着表面传播，同时这种耦合模式也表现出金属表面等离激元所具有的特性.因此在很长的一段时间内金属表面等离激元得到了广泛研究，并且基于表面等离激元提出了各种光学应用，如波导[4]、拉曼增强[5]、太阳能电池[6，7]等.但是金属中很强的欧姆损失限制了表面等离极化激元的传播程，也限制了金属表面等离激元的应用.而二维材料的出现为等离激元的应用带来了新的契机.尤其是石墨烯的出现，由于其独特的二维结构和电子结构[8]，呈现出独特的物理性质，如高的电子迁移率、对可见光的高透明度、室温量子霍尔效应等.石墨烯中的等离激元有着比金属表面等离激元更优异的光学性质[9]，如二维结构使得石墨烯中的等离激元具有更高的局域性和近场增强、高的载流子迁移率使得石墨烯中等离激元有更大的传播程、线性能谱使得石墨烯中等离激元频率相对于真空中电磁波波长更小.另外石墨烯中的等离激元频率覆盖了太赫兹到红外波段[10]，而且其模式可以很方便的通过门电压调节电子浓度来调节.石墨烯中的等离极化激元是石墨烯中等离激元和入射光的耦合模式，这种耦合模式也会表现出等离激元的光学特性[11].因此使得石墨烯被提出用于各种等离激元光学装置，如太赫兹辐射装置[12]、太阳能电池[13]、波导[14]、高灵敏传感器[15]等.

但是，由于自由空间的电磁波和石墨烯中等离激元的能量、动量不匹配(相同能量下，自由空间电磁波的动量远小于等离激元的动量)，因此两者不能直接耦合，因此要实现入射光对石墨烯中等离激元的激发和两者的耦合，需要一定的耦合机制.目前文献上提出了多种耦合机制，如光栅耦合[16]、棱镜耦合[17]、近场耦合[18]、表面声波耦合[19]等.同样，在法布里-珀罗谐振腔内也可以实现两者的耦合[11，20]，在该方法中，石墨烯系统放在谐振腔中作为等离激元的载体，和谐振腔提供的谐振腔电磁模式(腔模)光子可以发生耦合.但是文献上并没有关于腔模的详细研究，也没有考虑石墨烯的介电性质对腔模以及耦合的影响.本文基于麦克斯韦方程理论，计算了谐振腔中电磁模式，其次进一步研究了石墨烯在谐振腔中对腔模的影响，并得到了谐振腔中石墨烯的等离极化激元模式.

1 理论考虑与方法

我们考虑如图1所示的理论模型，石墨烯放在SiO2衬底上，系统处于法布里-珀罗光学谐振腔中.石墨烯作为等离激元的载体，谐振腔提供和石墨烯中等离激元耦合的腔模电磁模式，两者在石墨烯平面中耦合形成等离极化激元模式并沿着石墨烯表面传播.无规相近似下石墨烯中等离激元的色散关系[10]为ωp=(2e2γq/ћ2ε1)1/2(πne)1/4，其中γ=ћvF，vF=1.0×106cm/s，q为等离激元波矢的大小，ne为石墨烯中电子的浓度.ε1=(ε∞+εSiO2)/2是石墨烯层的有效介电常数，ε∞≃1.0是石墨烯层的高频介电常数,εSiO2=4.0为SiO2的介电常数.

图1 装置示意图:放在衬底SiO2上的石墨烯系统处于法布里-珀罗谐振腔中.谐振腔的长度为L,PL和PoL分别表示石墨烯中的等离激元和耦合形成的等离极化激元模式Fig 1 Device:the system consist of graphene and SiO2 substrate in Fabry-Pérot cavity. L,PL and PoL are respectively pres-ent the length of cavity, plasmon and plasmon polariton in graphene.

入射光在谐振腔里垂直于反射面的方向上经过界面的多次反射形成驻波.因此在垂直于反射面的方向上入射光是量子化的.我们考虑TM-偏振且偏振在x方向的入射光垂直入射到谐振腔中.由于此模型中石墨烯层加上SiO2厚度远小于腔模电磁波的波长，因此这里我们取石墨烯系统的介电常数为真空介电常数ε0≃1.0.在高斯单位下，入射光的的麦克斯韦方程可以表示为[21]

(1)

这里我们代入了E和H～exp(ikxx-iωt).在没有石墨烯层的情况下，麦克斯韦方程组的解可以写成

Ex(z)=Aexp(ikzz)+Bexp(-ikzz)

(2)

(3)

即得到

(4)

因此谐振腔中电磁波的模式为

(5)

方程(3)中，kx为腔模光子在石墨烯平面的波矢.

当石墨烯层置于腔内时，麦克斯韦方程组的解应满足腔的边界条件，即当z≥0时

(6)

以及当z≤0时

(7)

另一方面，石墨烯片的存在引入了跨越石墨烯层的边界条件，即

(8)

σ(ω)是石墨烯的光电导.结合方程式(6～8)，可以得到

(9)

在太赫兹频段内，石墨烯的光电导率主要是由导带内跃迁的自由载流子光吸收引起[22]，可以用Drude公式表示

(10)

τ是石墨烯的动量弛豫时间,主要由包括电子-杂质、电子-声子的散射机制造而成.把σ(ω)的虚部代入方程(9),石墨烯层存在时的腔模的色散关系可以通过解下面的方程得到.

(11)

2 结果和分析

众所周知，在石墨烯中由于杂质和声子散射导致的电子的室温动量弛豫时间是τ=0.1ps[23].同样τ也和石墨烯的电子密度有关[24].在图2中，我们给出了固定腔长下，腔内存在石墨烯层和不存在石墨烯层时的基态腔模的色散关系.q和kx分别是石墨烯中等离激元的波矢和入射光在石墨烯平面内的波矢.从图中可以看到：(1)低频腔模受石墨烯层的影响相对较大，而较高频率的腔模受石墨烯的影响较小.(2)随着石墨烯中电子弛豫时间的增加，石墨烯层对低频腔模的影响变大.(3)总体来看，在太赫兹频段内，石墨烯的存在对腔模的影响较小.(4)相同电子密度的情况下，无规项近似下(RPA)得到的等离激元色散关系曲线可以和在非高频近似的情况下得到的腔模色散曲线相交，因此两者可以在石墨烯平面内发生耦合.(5)图2中短-点-点虚线对应方程(9)的高频极限结果.即当ωτ>>1时,方程(9)中的光电导率σ(ω)取为

(12)

其值和τ无关.可以看到在高频近似的情况下，等离激元的色散曲线和腔模色散曲线不能相交.需要注意的是,在石墨烯中导带内电子的跃迁主要发生在入射光的THz频段内，因此在THz频段内和室温条件下,石墨烯中可以保证ωτ≈1，而高频极限Drude公式不能用于表示石墨烯中带内跃迁通道产生的光电导率.因此在高频近似的情况下，由于光电导率被高估，等离激元的色散曲线和腔模色散曲线不能相交.

图2ωp是无规项近似下(RPA)石墨烯中等离激元的色散曲线.基态腔模的色散关系:实线对应腔内不存在石墨烯的情况(方程(5)的结果)；其他线对应腔内存在石墨烯的情况(方程(9)的结果)，其中短-点-点虚线为方程(9)(ωτ>>1)取高频近似下的结果；短-点、短、点虚线对应电子弛豫时间分别为τ=1.0ps、0.5ps、 0.2ps的情况.

Fig.2ωpis the dispersion relation of plasmon in graphene in Random Phase Approximate(RPA).The dispersion relation of ground cavity modes: the solid line is result of without graphene in cavity(the result of equation (5)).Other lines are the results of with graphene in cavity(the result of equation (9)) and the dash-dot-dot line is the result of equation (5) in the limit of high frequency.The dash-dot, dash and dot lines are respectively the results of electron relaxation timeτ=1.0ps、0.5ps、0.2ps.

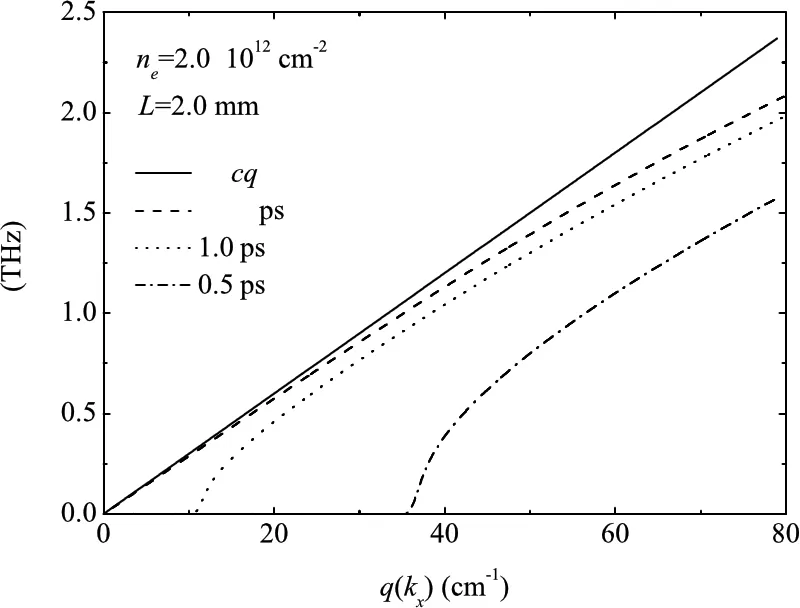
图3 实线：自由光子的色散关系曲线ω=cq.短、点、短-点虚线分别是τ>>1ps,τ=1ps和τ=0.5ps时石墨烯等离极化激元模式的色散关系.

Fig.3 Solid line: the dispersion relation of free photons.The dash,dot and dash-dot lines are the dispersion relations of plasmon polariton in graphene correspond to respectivelyτ>> 1ps,τ=1ps,andτ=0.5ps.

(13)

求解该方程即可得到谐振腔内石墨烯的等离极化激元模式.

我们注意到，这种方法也是通常用于计算金属表面等离极化激元模式[25].在图3中，我们展示了谐振腔内不同电子弛豫时间下石墨烯等离极化激元模式的色散关系.可以看到，等离极化激元模式的频率总是低于自由空间光模式的频率(即ω=cq).更重要的是，在有限的τ情况下，石墨烯中只存在非零波矢q的等离极化激元的模式，而且截止频率随τ的减小而增加.因此，谐振腔中石墨烯等离极化激元模式只能在谐振腔内以相对较大的波矢q存在.

3 结论

本工作中我们利用麦克斯韦方程计算得到了法布里-泊罗谐振腔中腔膜光子的频率模式.并且我们研究了谐振腔中存在石墨烯时，石墨烯层对腔膜光子的频率模式的影响.研究表明石墨烯层的存在对腔内光子模式的影响较小.在合适的腔长和石墨烯中电子浓度下，石墨烯中等离激元的色散曲线和腔膜光子的色散曲线可以相交，意味着两者可以在石墨烯平面耦合从而形成等离极化激元.同时我们得到了谐振腔中石墨烯等离极化激元的模式，结果表明在经典麦克斯韦方程理论下，谐振腔中的石墨烯中只存在非零波矢q的等离极化激元的模式.该工作对于深刻理解谐振腔中石墨烯的等离激元光学性质以及该结构应用于等离激元装置具有一定的理论意义.