定向超图逆Perron值的若干上界

汪乐，徐静

(安徽大学 数学科学学院，安徽 合肥 230601)

近年来，超图谱的研究引起了广泛的关注,越来越多的学者通过张量(邻接张量,拉普拉斯张量等)来研究超图谱的性质[1-4]。一个k阶n维实张量A=(ai1i2…ik)是由nk个实元素ai1i2…ik组成,这里ij∈[n]([n]=1,2,…,n),j∈[k].超图G=(V(G),E(G)),其中顶点集V(G)={v1,v2,…,vn},边集E(G)={e1,e2,…,em},ej⊆V(G),∀j∈[m].如果顶点v∈e(e∈E(G)),称v和e是关联的。若对任意的j∈[m]均有|ej|=k,称G为k一致超图。对于G中任意一点v∈V(G)d(v)=|{ej:v∈ej}|为顶点v的度,称{d1,d2,…,dn}是G的度序列。对于G中任意两点u,v∈V(G),从u到v的路定义为点与边均不重复的交替序列v1,e1,v2,…,ed,vd+1其中v1=u,vd+1=v并且vi∈ei,vi+1∈ei,∀i∈[d].若G的任意两个顶点都有一条路连接, 则称G是连通超图。超图G的k阶n维邻接张量A(G)[3]定义为A(G)=(ai1i2…ik)其中

设D(G)为k阶n维度对角张量, 对角元素为dii…i=d(vi),∀i∈[n]。

类似于超图拉普拉斯张量,Gσ的拉普拉斯张量定义为L(Gσ)=D(Gσ)-A(Gσ),其中D(Gσ)是k阶n维度对角张量。一般,对于一个n维实向量x∈Rn实数Axk和n维向量Axk-1的定义如下:

与定向超图邻接张量相类似, 根据定向超图拉普拉斯张量的定义,容易得到

卜长江[7]等介绍了一致超图的逆Perron值aj(G),通过aj(G)刻画一致超图的连通性。本文将逆Perron值aJ(G)推广到定向超图。定义定向超图的逆Perron值aj(Gσ)如下:

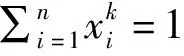
1 主要结论

定理1.1设Gσ是有n个顶点和m条边的定向超图,{d1,d2,…,dn}是Gσ的度序列。对任意顶点j,我们有

证明对任意顶点j∈V(Gσ), 设向量x=(x1,x2,…,xn)T满足

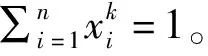
定理1.2设定向超图Gσ有n个顶点和m条边,{d1,d2,…,kn}是Gσ的度序列,则对任意的顶点j,我们有

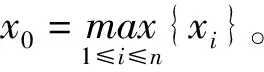
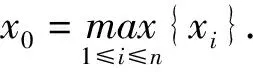
我们有

aj(Gσ)≤L(Gσ)xk

通过均值不等式可以得到

我们容易得到

定理1.3定向超图Gσ有n个顶点和m条边,则对Gσ中任意的顶点j∈V(Gσ),我们有

证明对于任意一个顶点j∈V(Gσ),设e0={j1,j2,…,jk}是Gσ中的一条边并且j∉e0,向量x=(x1,x2,…,xn)T满足

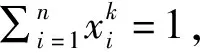
aj(Gσ)≤L(Gσ)xk

2 结束语

定向超图逆Perron值上界的刻画有很多种，本文利用定向超图的顶点数、边数、度序列和逆Perron向量来刻画，对于定向超图的其他不变量, 如定向超图的最大度、定向超图的直径等, 也可以利用本文的方法类似地刻画定向超图逆Perron值的上界。