需求扰动下制造商主导的闭环供应链超网络均衡决策研究

李昌兵，宋美仪，张婷婷 LI Changbing, SONG Meiyi, ZHANG Tingting

（重庆邮电大学 经济管理学院，重庆400065）

0 引 言

近年来，我国大力提倡环保，将生态文明建设纳入国家建设的总布局中，加大对各企业生产制造的监督，使得越来越多的制造企业更加重视资源回收利用对环境保护的重要性。对资源进行回收利用不仅关乎制造企业，也关系到整个闭环供应链网络的运作和管理。目前，大部分学者主要研究闭环供应链的定价和协调问题、闭环供应链的回收决策问题和闭环供应链中企业社会责任问题等[1-3]。在实际生活中，当一些突发事件（流感病毒）、自然灾害（2008 年汶川地震、台风等） 发生时，如果供应链中的各层企业不调整生产和销售计划，就会对供应链网络造成巨大的影响，导致惨重的损失。因此在闭环供应链管理中，如何采用有效的措施应对需求扰动带来的影响，其重要性不言而喻。韩小花等[4]在零售商竞争的闭环供应链中，研究了成本和需求同时扰动对供应链各层企业产生的影响。Pan 等[5]研究了当需求或成本发生扰动时，通过调整合同的参数来实现对双渠道供应链中断的协调。汤春华等[6]研究了需求扰动下供应链上各层企业的行为决策，采用收益共享契约进行协调。Tang 等[7]研究了同时中断需求和成本对由一个制造商和一个零售商组成的双渠道供应链的定价、生产和协调的影响，利用收益分享合同进行协调。以上研究只考虑需求或生产成本扰动对由单个制造商、零售商组成的双渠道供应链或闭环供应链均衡决策的影响，并未考虑到多个制造商、零售商以及其他供应链成员。考虑到以上问题，本文针对由多个制造商、多个零售商、多个需求市场和多个回收商组成的闭环供应链网络，建立稳定环境和需求扰动下的闭环供应链网络模型，然后进行数值算例分析，讨论需求扰动对各层企业交易量和需求价格的影响。

1 模型构建与符号说明

1.1 模型构建

本文构建的闭环供应链模型由M个制造商，N个零售商，K个需求市场以及R个回收商4 个层次组成，该网络系统中存在不同层的纵向合作。该闭环供应链包括正向供应链和逆向供应链，回收商是将正、逆向供应链连接起来的网络节点。在该网络中，制造商负责采购原材料、生产新产品和再制造产品，以及将生产过程中产生的废弃材料送往报废中心；零售商负责将制造商生产的产品销往需求市场；回收商负责回收旧产品并将旧产品转卖给制造商。由于在闭环供应链中存在一些不确定因素，故给出如下假设：（1） 各企业都是理性的，都追求自身利润最大化和偏离成本最小化；（2） 仅考虑制造或回收一种产品或完全可替代品，其中再制造品和新产品没有本质的区别；（3） 该闭环供应链由制造商主导，同层决策者处于非合作竞争状态；（4） 相关成本函数均为连续可微的凸函数。

1.2 符号说明

相关变量及说明如表1 所示：

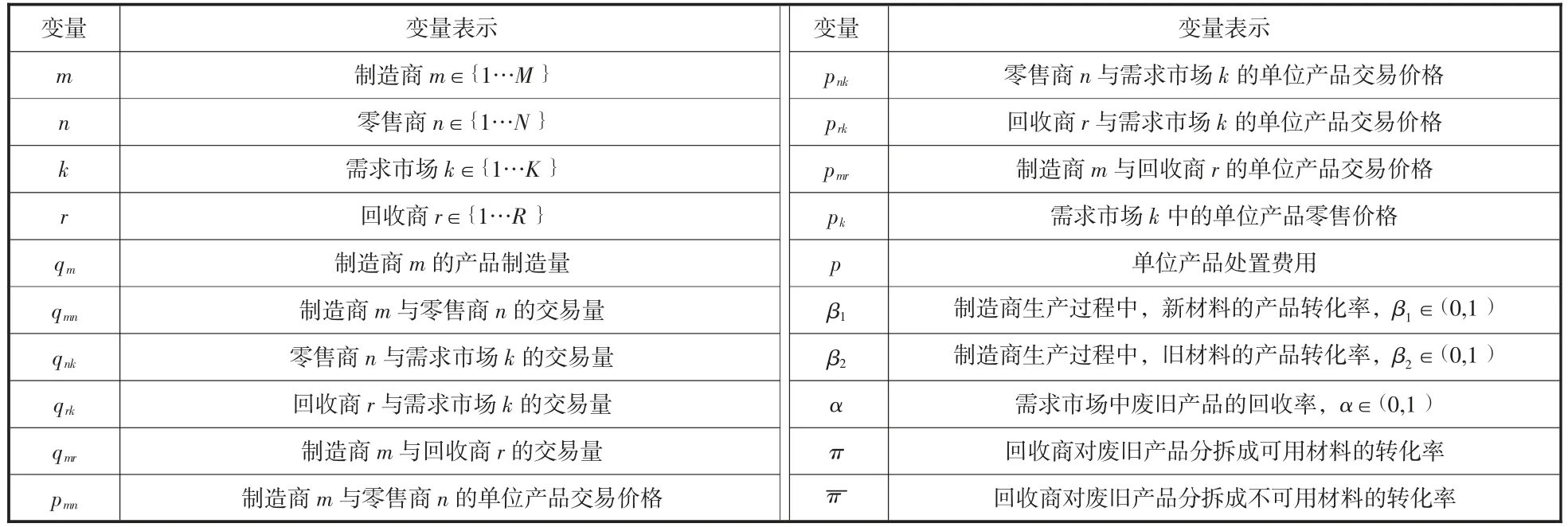
表1 相关变量及说明

2 需求扰动下制造商主导的闭环供应链超网络均衡模型

由于本文研究的是需求扰动对闭环供应链网络均衡的影响，故本文只呈现了需求扰动下闭环供应链网络均衡模型，而没有呈现稳定环境下闭环供应链网络均衡模型。在有无需求扰动下模型的建立方法相似，两者的差别在于需求扰动下需考虑企业由于调整计划产生的偏离成本，在数值算例部分会对两种情形进行仿真实验。

当需求扰动发生时，信息传递到网络中的各层次企业后，各企业需要调整计划来应对扰动带来的影响，调整计划会产生额外的偏离成本。需求扰动发生后，各企业追求利润最大化和偏离成本最小化的目标。作为闭环供应链的主导企业，制造商承担所有的偏离成本[4]。

2.1 制造商的行为决策及最优目标分析

需求扰动发生后，制造商m将产品卖给零售商n获得的收益为pmn qmn，制造商m与供应商i、零售商n、回收商r的交易成本分别为制造商m的采购成本为fm qm（ ），新旧材料生产成本分别为由于调整计划产生的偏离成本为本文采用权重为1 的标准权函数，则制造商m的目标函数为：

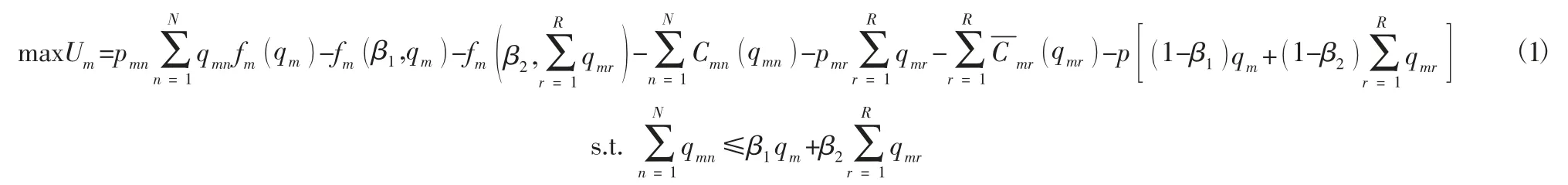
同时，制造商还追求偏离成本最小化，则目标函数为：

假设式（1）、式（2） 中的函数都是连续可微的凸函数，则制造商m的最优解为该式应满足如下变分不等式：

λ1是保证变分不等式（3） 成立的拉格朗日系数。

2.2 零售商的行为决策及最优目标分析

需求扰动发生后，零售商n将产品销往需求市场k获得的收益为pnk qnk，零售商n与制造商m、需求市场k的交易成本为零售商n的产品存储费用为同2.1 方法一样，则零售商n的目标函数为：

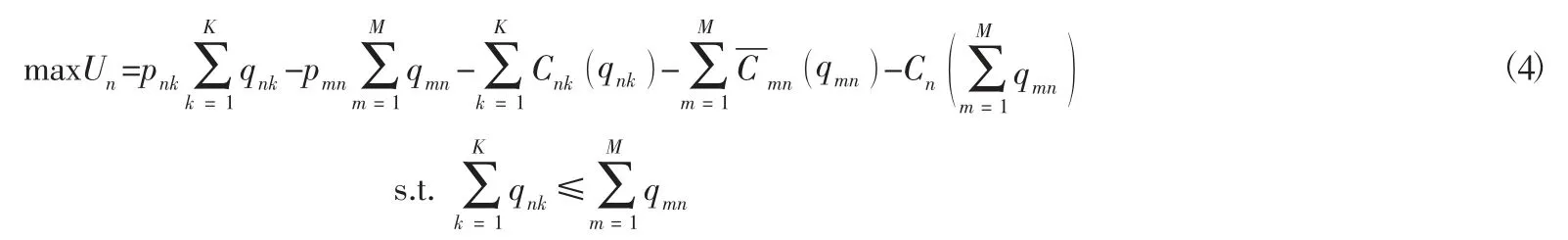
假设式（4） 中的函数都是连续可微的凸函数，则零售商n的最优解为该式应满足如下变分不等式：

λ2是保证变分不等式（5） 成立的拉格朗日系数。

2.3 需求市场的均衡条件

需求市场k的产品需求函数为Dk Pk（），设Δdk为需求扰动量，Δdk≥0 表示需求市场中的消费者对产品的需求量相对于稳定环境下增多了；Δdk≤0 表示需求市场中的消费者对产品的需求量相对于稳定环境下减少了。本文用Δd表示所有需求市场上产品的需求扰动量构成的列向量，Δd= （Δd1,Δd2,…,Δdk）T[8]。同2.1 方法相同，那么需求市场k的均衡条件为：

式（6） 表示在均衡条件下，如果需求市场中的消费者愿意购买此类产品，则此时需求量等于供给量；当供给量大于需求量时，此类产品的需求价格为零。式（7） 表示当零售商与需求市场的单位产品交易价格和单位交易成本不超过产品的单位需求价格时，需求市场与零售商进行交易；否则，不进行交易。

式（8） 说明当需求市场与回收商之间的单位交易成本不超过产品的单位交易价格时，需求市场与回收商进行交易；否则，不进行交易。约束条件表示回收商向需求市场回收的产品总量不能超过需求市场的供给量，其中，α 为产品的回收率。

假设式（6）、式（7）、式（8） 中的函数都是连续可微的凸函数，那么需求市场k的最优解为该式应满足如下变分不等式：

λ3是保证变分不等式（9） 成立的拉格朗日系数。

2.4 回收商的行为决策及最优目标分析

需求扰动发生后，回收商r将旧产品卖给制造商m获得的收益为pmr qmr，回收商r与需求市场k、制造商m之间的交易成本分别为回收商r承担的收购、运输、存储费用为同2.1 方法一样，则回收商r的目标函数为：

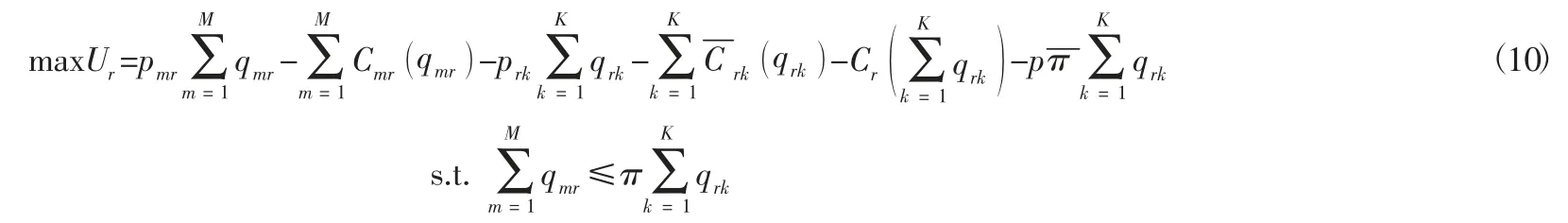
假设式（10） 中的函数都是连续可微的凸函数，则回收商r的最优解为该式应满足如下变分不等式：

λ4是保证变分不等式（11） 成立的拉格朗日系数。

2.5 需求扰动下模型动态均衡分析

由上述公式可知，该闭环供应链超网络模型的动态均衡状态存在的唯一解为并满足如下条件：

证明：将式（3）、式（5）、式（9）、式（11） 相加化简便得到式（12）。如果在式（12） 的第一个中括号中加上第二个中括号中加上第三个中括号中加上第四个中括号中加上第五个中括号中加上并不会影响式（12） 的解，因此式（12） 的解为式（3）、式（5）、式（9）、式（11） 之和，证毕！最后利用梯度投影算法求解连续凸函数的变分不等式的解。

3 数值算例

为了研究需求扰动对该闭环供应链的影响，假设该网络由两个制造商、两个零售商、两个需求市场和两个回收商组成。设β1=0.4，β2=0.6，α=0.8，p=2, π=0.4，=0.6，具体函数如下：

（1） 制造商m（m=1,2 ），采购函数fm（qm）

（2） 制造商m（m=1,2 ）利用新材料的生产成本函数fm（β1,qm）

（3） 制造商m（m=1,2 ）利用旧材料的生产成本函数

（4） 零售商n（n=1,2 ）的产品存储成本函数

（5） 回收商r（r=1,2 ）的产品收购、运输和存储费用函数

（6） 零售商n（n=1,2 ）与需求市场k（k=1,2 ）的交易成本函数Cnk（qnk）、需求市场k（k=1,2 ）与回收商r（r=1,2 ）的交易成本函数Crk（qrk）、制造商m（m=1,2 ）与回收商r（r=1,2 ）的交易成本函数Cmr（qmr）

（7） 制造商m（m=1,2 ）与零售商n（n=1,2 ）的交易成本Cmn（qmn）

（8） 需求市场的产品需求函数Dk Pk（）

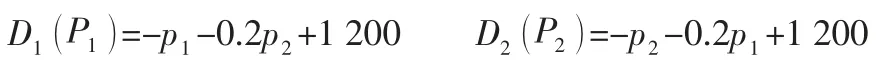
3.1 稳定环境下的均衡结果

将以上函数代入建立的模型中，运用MatlabR2016a 软件编程，进行仿真实验。设置迭代的步长为0.01，计算精度为0.001。稳定环境下，得到的实验结果如表2 所示：

表2 稳定环境下闭环供应链网络均衡结果

3.2 需求扰动下的均衡结果

假设需求市场2 不发生需求扰动，需求市场1 的需求扰动量为Δd1, Δd1= ｛-100,-80,-60,-40,-20,0,20,40,60,80,100 ｝。此时，需求市场2 的需求函数不变，需求市场1 的需求函数变为D1（P1）=-p1-0.2p2+1 200+Δd1。对上述算例进行仿真。

（1） 需求扰动对闭环供应链均衡结果的直接影响。需求扰动对闭环供应链均衡结果的直接影响是指：在该闭环供应链网络中，需求市场1 发生了需求扰动，所以需求扰动直接地对制造商1、零售商1、需求市场1 以及回收商1 之间的交易量产生了影响。如图1 所示，当需求扰动量增加时，制造商1—零售商1、零售商1—需求市场1、需求市场1—回收商1 以及回收商1—制造商1 之间的交易量也增加了，因此交易量与需求扰动呈正相关。

图1 各层企业的交易量随需求扰动量的变化

从图1 还可以看出，随着需求扰动量的增加，零售商1—需求市场1、需求市场1—回收商1 的交易量也随之增加，并且增加的幅度较大；而制造商1—零售商1、回收商1—制造商1 的交易量变化幅度较小。这是因为零售商1、回收商1 与需求市场1 最接近，他们可以快速地收到需求扰动发生的消息，然后调整各自的销售和回收计划，他们之间的交易量的变化很直接地反映出当前需求扰动的程度。作为该闭环供应链的主导企业，制造商1 会根据零售商的订单消息和回收商的回收情况来调整他的生产和销售计划。由于制造商1 掌握了大量的信息，可以做出较优的决策，因此制造商1 面对需求扰动的干扰时，具有一定的抗干扰性，与其他层企业的交易量受到的影响就较小。

面对需求扰动的发生，制造商与零售商、制造商与回收商之间可以通过签订契约，如采用收益共享契约、数量折扣契约等来减小扰动因素带来的冲击。

（2） 需求扰动对闭环供应链均衡结果的间接影响。选取实验结果中的部分数据，如表3 所示。表3 中的数据说明，需求市场1 发生的需求扰动间接地对制造商2、零售商2、需求市场2 以及回收商2 之间的交易量产生了影响。当需求扰动量减少时，零售商2—需求市场2、需求市场2—回收商2 的交易量增加了。这是因为随着需求扰动量的减少，即需求市场1 中的消费者对产品的需求减少了，零售商1—需求市场1、需求市场1—回收商1 的交易量减少了，这就意味着需求市场2 中的需求有所增加，需求市场2 与零售商2、回收商2 的交易量增加了。

表3 需求扰动涟波效应

表3 中的数据还说明，当需求市场1 的需求减少时，需求市场1、2 的需求价格均在减少，市场1 的需求价格减少幅度更大；当需求市场1 中的需求增加时，需求市场1、2 的需求价格均在增加，市场1 的需求价格增加幅度更大。由此可得，当需求扰动发生时，对于整个供应链网络来说，发生扰动的供应链受到的影响更大，同时整个闭环供应链都会受到冲击。因此，当整个供应链网络受到外界干扰时，局部的扰动会波及全局，需求扰动对供应链网络造成的间接影响恰好表现在需求扰动具有很强的涟波效应。

4 结束语

在基于稳定和需求扰动环境下，本文建立了闭环供应链超网络模型，并研究了闭环供应链网络中各层企业的行为决策和最优目标，利用变分不等式理论以及梯度投影算法求出系统网络的均衡点。通过数值算例分析，得到以下结论：（1） 当需求扰动发生时，发生需求扰动的供应链中各层企业交易量的变化与需求扰动呈正相关，需求市场的需求价格也与需求扰动呈正相关。其中，直接与需求市场发生交易的企业受到扰动的影响更大。（2） 当供应链网络中的其中一个需求市场发生需求扰动时，不仅该供应链受到影响，而且其他供应链也会被波及。因此在需求扰动发生时，各层企业可以通过签订相关契约，如收益共享契约、数量折扣契约或共享信息等来协调供应链，减小需求扰动对供应链产生的影响。