随机需求下干线交叉口的自适应协调控制研究

姚 佼，韦 钰，王品乘，邵楚薇 YAO Jiao, WEI Yu, WANG Pincheng, SHAO Chuwei

（上海理工大学 管理学院，上海200093）

0 引 言

自适应控制是动态响应交通需求波动，通过实时交通测量和对未来交通需求的实时预测改变调整控制方案。协调控制有助于交叉口间的联动，改善城市道路交通拥堵，减少出行时间。目前协调控制的研究主要是对相位差，协调绿波带宽进行优化，随机需求波动条件下，如何将自适应与协调控制有效结合，提高干线通行效率，更具实用价值。

协调控制方面，国内外研究主要集中对相关经典模型及参数的优化方面。Sheffiy 在交通均衡流方面进行了深入研究；Watling 概括了现有的一些均衡分配方法，解决了出行者对变化交通状况处理的问题[1]。在给定的交通状况和条件下；Yin 等人提出了绿灯时间分割的概念，对时间参数进行分解和优化，减少时间延迟[2]；Chiou 首先研究了确定条件下基于数据和模型的分析[3]，进而提出了一种拟牛顿投影法，来减少延误，使出行时间减少[4]；Huang 等人采用了控制迭代的方法，得到最优的路径选择[5]。这些方法都是在给定或已知条件下进行研究的，但路段上的流量往往具有不确定性和随机性，因此，自适应控制被引入到本领域的研究[6]。

自适应控制国内外的研究主要集中在运用两阶段规划等方法研究单个交叉口的自适应控制。许伦辉等人对单个交叉口的模糊控制进行研究和分析，有效地减少了车辆的平均延误[7]；Tong 等人提出了一种自适应信号时序规划模型，使车辆的预期延误最小化[8]；刘广萍等人对交通自适应信号控制下交叉口延误的计算方法进行了研究，得到交叉口延误[9]；Lo 在自适应控制模型中设置了一个缓冲区，减少溢出现象，使得出行时间尽可能小[10]；李媛等人则是通过双向优化相位差的方法，得出车辆的车均延误[11]；Huang 等人提出了两阶段随机规划的方法，得到最小出行时间[12]。

综上可以看出，大多研究主要着重于整体交通网络均衡或单交叉口相位差和干线绿波[13]的协调，如何将两者有效的结合，考虑到交叉口间的随机波动进行协调控制，值得进一步探讨。

研究基于两阶段随机规划模型，第一阶段将考虑路段均衡流，第二阶段在需求不确定的情况下，调整干线交叉口间的偏移量，协调绿灯时间，确定自适应协调控制的决策，解决偶发性的溢出，避免拥堵现象的发生。

1 第一阶段考虑路网均衡流量优化的干线交叉口协调控制模型

第一阶段是在固定配时方案下，考虑路网均衡的流量优化，路段车均出行时间用式（1） 表示为：

式中：t（xa,Gi）为路段车均出行时间，为路段a自由流的出行时间；xa为路段a上的流量；Gi为交叉口i的绿灯时间；sa为路段的饱和流；c为i交叉口的周期；α 和β 为参数，根据相关参考文献[12]，一般取α=0.15, β=4。

据此，目标函数路段总的出行期望时间可以用式（2） 表示为：

式中：E［h（xa,Gi）］为最小总出行期望时间。

本阶段主要分为两个步骤进行：

（1） 将干线交叉口信号设计问题以一个两阶段随机规划形式表示，找到路段车均出行时间的最优解。具体而言，先要找到路段流量的最优解，再进行对绿灯时间进行优化协调控制，使路段流量达到平衡。

主要步骤如下：

式中：αn为第n次优化长度的大小，0≤α≤1；yn

a为路段a上第n次移动的长度；路段第n+1 次的总流量；λ 为参数；qrs为r-s路段上的总流量；为所有OD的总流量；为r-s路段上的随机变量。

Step4：流量更新，如式（4） 和式（5） 所示：

（2） 在没有随机需求的情况下，交叉口运用的是基本控制方案，绿灯时间固定，当随机流量或者溢出流出现时，流量和绿灯时间发生变化，交叉口的排队长度增加，通过调整偏移量，协调交叉口的绿灯时间，减少溢出流的现象。

根据路段上的流量情况可分为（如图1 所示） 三种情况的时间—流量图，第一种情况是交叉口的绿灯时间完全可以清除上一阶段剩余的排队长度；第二种情况是交叉口绿灯时间不能完全清除上一阶段的剩余排队车辆，还有随机车流的出现，需要调整偏移量，协调出最佳的绿灯时间和控制方案，减少排队车辆，下一阶段不会发生溢出现象；第三种情况是交叉口不能清除上一阶段的车辆，还有随机车流的出现，交叉口的绿灯时间无法清除排队车辆，导致下一阶段发生堵塞或是溢出的现象。第一种情况不会发生拥堵和溢出现象不予考虑，第三种情况堵塞和溢出更加严重，所以也不予考虑。本文主要研究第二种情况，使交叉口的排队车辆尽可能少，减少拥堵和溢出。

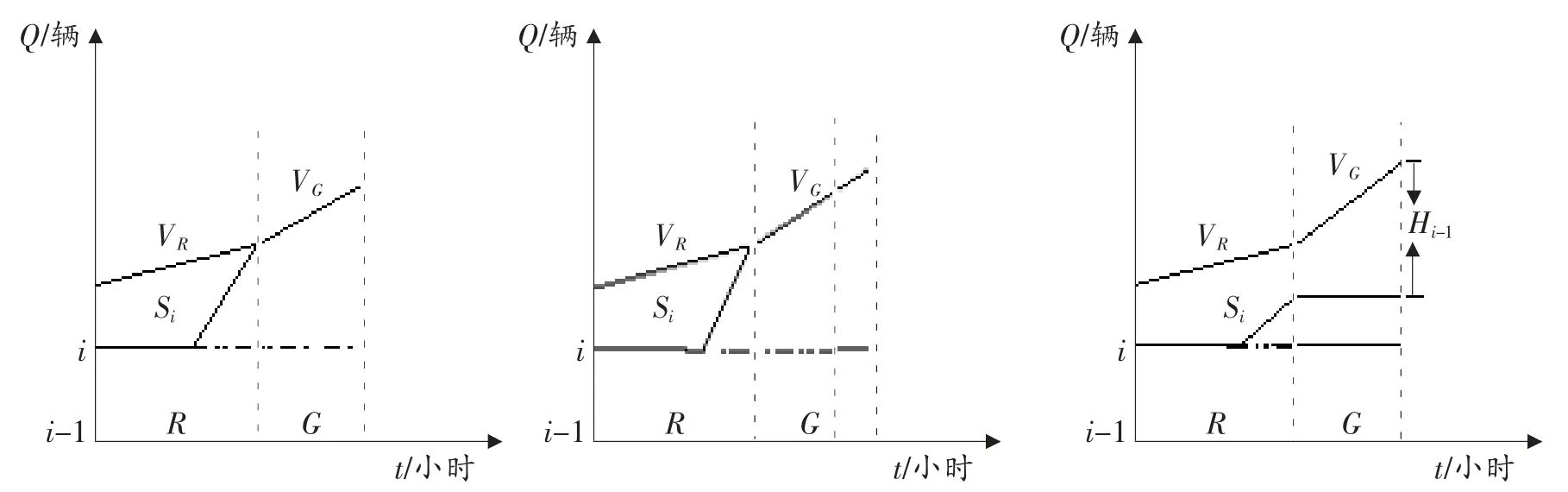
图1 流量与红绿灯时间分布图

2 第二阶段考虑随机需求波动的干线交叉口自适应协调控制模型

考虑干线相邻两交叉口间有车辆汇入汇出的情况，会引起流量的随机波动，假设汇入相邻两交叉口干线的流量符合一种已知的分布函数，由于流量的波动，偶尔会引起堵塞或溢出现象，通过干线的自适应协调控制，使路段出行时间减少。当有随机流量出现时，就要通过调整偏移量来改变绿灯时间如图2 所示。

图2 两交叉口红绿灯时间协调分布图

第二阶段是考虑路网均衡的流量优化，路段车均出行时间用式（6） 表示为：

绿灯时间、偏移量和清空时间三者之间的关系如式（7） 和式（8） 所示：

式中：CT为清空时间；O为偏移量；Gi-1为i-1 交叉口的绿灯时间；Ti为标准偏移量。

准偏移量和清空时间的表示如式（9） 和式（10） 所示：

式中：L为两相邻交叉口间干线的距离；v为干线车辆行驶速度；vR为红灯时间内交叉口i的车辆到达率；Ri-1为i交叉口的红灯时间；si为i交叉口的车辆离开率。

绿灯时间范围CT≺Gi≤CT+Gi-1。

加入随机需求考虑的情况，干线路段上优化后的总流量如式（12） 所示：

式中

式中：ω 为参数，可根据路段的实际情况判定，一般取0.80。

最终的目标函数如式（13） 所示：

3 案例分析

选取上海黄浦区西藏南路（淮海中路—寿宁路段） 的干线沿线交叉口，如图3 所示，基于实地调查的实际数据，该干线高峰期间车流量较大，饱和度较高，此外沿线单位进出口等亦较多，容易产生随机波动，符合本研究模型的要求。

图3 研究西藏南路干线沿线交叉口分布图

（1） 第一阶段未考虑随机需求的分析结果

没有优化流量之前的信号配时方案是固定的：将相关参数Gi=77 秒，Ri=30 秒，xa=1 152 辆，=5 分钟代入式（1） 得到第一阶段未考虑随机需求时路段车均出行时间0.18 小时，总出行期望时间为203.90 辆*小时。

对路段流量进行优化，车辆流量方向从南往北行驶，从寿宁路交叉口往淮海中路的方向。当收敛趋近于零时，迭代停止。流量优化的结果如表1 所示。

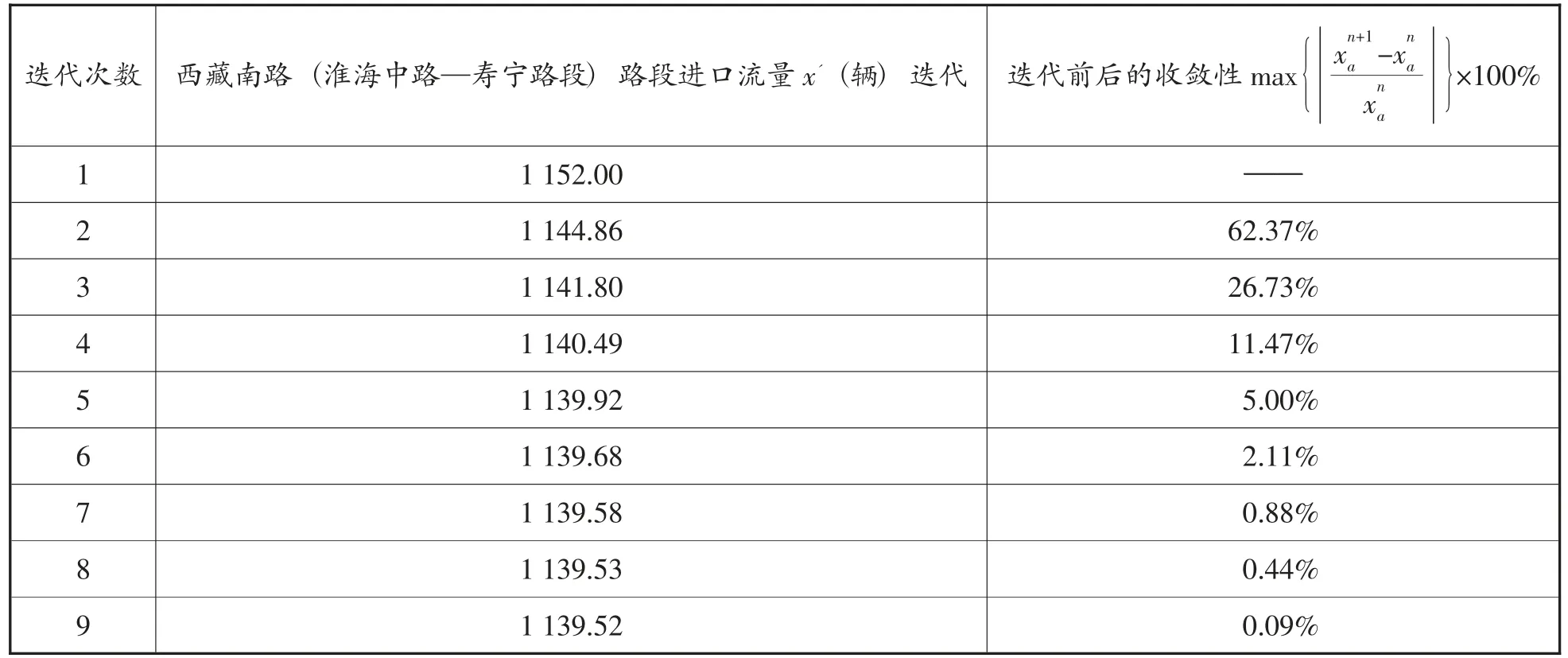
表1 干线路段流量迭代优化过程

从表1 可以看出，在信号配时方案不变的情况下，路段上流量优化结果为1 140 辆，对路段的车均行程时间，代入式（1）得到第一阶段流量迭代优化后的路段车均出行时间为0.18 小时，总出行期望时间为200.64 辆*小时。

由此可见，在交叉口配时方案不变，未考虑随机需求波动，仅考虑流量优化的情况下，干线上总期望出行时间减少了1.60%。

（2） 第二阶段加入随机需求波动的优化结果

对淮海中路交叉口的绿灯时间进行优化，两个交叉口相距约367 米，两个交叉口之间若干单位会有车辆的波动，干线上会有流量的增加，从而引起随机波动。两个交叉口信号控制方式中绿灯时间（Gi-1）为77 秒，红灯时间（Ri-1）为30 秒，两交叉口绿灯协调时间分布如图4 所示。

图4 两交叉口绿灯协调时间分布图

首先，基于调查的数据，将相关参数（L=367 米，v=25 千米/小时，Hi=9 辆，vR=950 辆/小时，Ri-1=30 秒，si=1 800 辆/小时） 代入式（9） 和式（10），得到的偏移量和清空时间分别为：

进而根据式（6） 得到偏移量O为17 秒。

其次，将上面得到的数据代入式（7） 得优化之后的绿灯时间为130 秒。

再次，根据调查相关数据，基于第一阶段路段流量优化的结果，同时根据式（11） 考虑干线沿线单位出入口进入主干道的车辆数为67 辆，将其代入式（12），得两阶段路段总流量的优化结果为1 207 辆。

最后，将上述计算结果代入式（6），得第二阶段考虑随机需求波动优化之后的路段车均出行时间为0.17 小时，将其代入式（13），得干线路段上总的出行期望时间为119.15 辆*小时。

据此，本研究考虑随机需求波动的自适应协调控制模型与现状的优化结果对比如表2 所示。从中可以看出，第一阶段未考虑随机需求波动，对路段流量进行均衡优化，路段车均出行时间减少0.56%；第二阶段，在考虑随机需求增加4.77%波动情况下，路段车均出行时间较第一阶段减少6.25%，较现状减少6.78%。

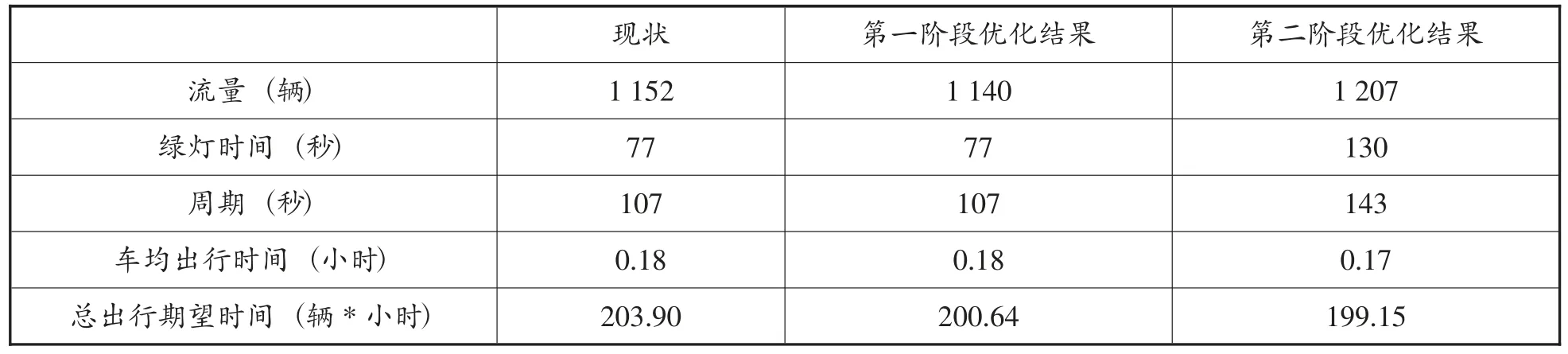
表2 考虑随机需求波动的自适应协调控制模型优化结果对比

路段总的期望时间上，第一阶段较现状减少了1.60%；第二阶段，考虑随机波动的情况下，较第一阶段减少了0.74%，较现状减少了2.33%。

4 结 论

针对干线交叉口间单位出入口造成的随机需求波动问题，本研究在分析干线随机需求及其主要影响因素的基础上，提炼出流量和出行时间两个关键因素，进而建立了两阶段随机规划模型，通过对路段流量、绿灯时间、偏移量等进行优化，达到了自适应协调控制的要求。最后通过相关的实际案例进行验证，结果表明，本研究的自适应协调控制模型在随机需求波动导致路段流量增加4.77%的情况下，可以使路段车均出行时间减少6.78%，总出行期望时间减少2.33%，有效提高了干线通行能力。

需要指出的是，随机波动和需求的变化程度对总出行期望时间的研究都有着很重要的影响，本文研究主要考虑干线交叉口间的协调，如何将其运用到路网中，进一步研究路网的服务可靠性问题，通过提高路网的可靠性减少期望出行时间，是后续研究需要关注的问题。