养成比较习惯：让数学课堂更真实

江苏省泗阳县临河小学 房开香

学生数学素养的形成，在很大程度上是通过让学生比较而获得的。让学生养成比较习惯，才能更好地发展学生的数学思维，才能让学生在数学课堂上达到真懂得、真运用，才能让我们的数学课堂更真实、高效。

一、在比较中归纳，形成知识技能

许多数学问题中都具有非常相近或者相似的地方，或者是存在着许多内在的联系。如果我们通过比较，让学生寻找它们之间的共性，那么学生就可以在比较中进行归纳与总结，把握数学知识的核心内容，进而理解这些内容，并形成新的数学知识与技能。

比如教学《乘法分配律》时，我先让学生计算这几组计算题：8×（5+9）与8×5+8×9；21×14+21×16 与21×（14+16）；18×15-18×5 与18×（15-5）；20×（23-7）与20×23-20×7。在学生算完之后，组织学生交流比较。

师：通过计算，大家发现了什么？

生：我发现每一组的两道算式计算结果都是一样的。

生：我通过比较发现每一组算式中，都只有三个数字，而且它们有一个共同特征，那就是由一个数字分别乘另外两个数字，然后再一起加减，或者用一个数字乘另外两个数字的和或者差，它们的结果是一样的。

生：如果我用字母分别表示这三个数字，那么它们都可以用这三个字母来表示：a×(b+c)=a×b+a×c或者a×(b-c)=a×b-a×c。

生：我通过比较发现，老师给我们的数字要么是两位数，要么是一位数，如果是三位数以上的计算，是不是也有这样的规律呢？

师：大家可以分别举几个三位数计算的例子，然后再一起比较一下，看看有什么规律。

……

在这一教学环节中，学生通过比较就会发现它们之间具有一定的规律，都可以用相同的含有字母的算式来比较。这样，新的知识点就在学生的比较中形成建模。而通过计算，学生发现三位数也同样适应这一规律，于是，乘法分配律的计算模型就在学生的脑海中形成了，为下面的教学奠定了基础。

二、在比较中辨析，理清知识异同

我们要通过比较来帮助学生辨析不同知识点之间的异同，发现它们之间的区别与联系，才能在学生的脑海中形成清晰的知识概念，在以后解决数学问题时才不会出现错误。

比如在教学“化简比”与“求比值”这一部分内容时，它们之间虽然有许多相同之处，但是它们之间是有区别的，它们思考的路径也是不一样的。为了强化它们之间的区别，我们可以通过比较来帮助学生理清知识间的差别，从而形成清晰的知识结构。

师：请同学们把4 ∶0.25 化成最简整数比，并求出比值。

学生计算之后，指名学生把自己的两种算法写在黑板上。

师：请同学们比较这两种算法，你认为化简比与求比值有什么区别呢？

生：求比值就是直接拿4 除以0.25 得16，化简比就是先把它们化成整数比4 ∶0.25=（4×100）∶（0.25×100）=400 ∶25=（400÷25）∶（25÷25）=16 ∶1，它们之间的意义与结果都是不同的。求比值最终的结果是一个数，而化简比最终的结果是一个比。

通过比较，学生不仅把化简比与求比值之间的区别给弄清楚了，还能够让学生在解决这两类问题时，有一个清晰的解题思路而不混淆。

三、在比较中链接，完备知识结构

面对相同或者相近的知识点，教材编写者总是根据它们的难易程度，由浅入深地安排在不同的年级，有时候相同的知识点安排可以相隔几个学期。这样，有时候学生学习后面的知识点时，前面的知识点就会忘记了。如果我们可以把这相同的知识点放在一起进行比较，那么就可以更好地激发学生的数学前经验，唤醒以前的知识结构，并把新的知识结构融入旧的知识结构之中，形成一种全新的完备知识结构。这样，学生在以后解决数学问题时才能从不同的角度来思考，最终寻找到一个适合自己的解决问题的方法。

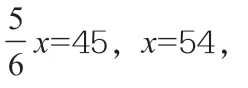
第二种解法：45÷5×6+45=99（棵）。

第三种解法：45÷5×（6+5）=99（棵）。

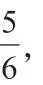
总之，比较可以让学生的数学思维更明朗，可以让数学教学更轻松，课堂教学效果更优化。我们要让学生在比较中学习数学，从而促进学生的数学学习真正发生，让数学课堂更真实、高效。