关注思维可视 选取有利支架

章华萍

【摘   要】思维可视化能使学生更好地理解和内化知识。要达到思维可视化，需要选取合适的可视支架。以“小数的初步认识”为例，通过对不同教材的具体引入素材和直观模型进行比较，能为选取有利于优化教学的可视化支架提供决策依据。

【关键词】小数;可视化支架;教材比较

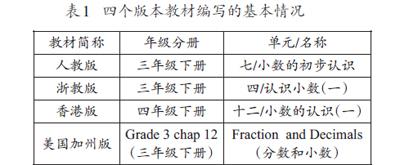
把思维如思考方法和思考路径那样运用各种图式呈现出来，是思维可视化的核心。思维可视化有利于学生对知识的理解和内化。在“小数的初步认识”一课中，学生认识小数的思维可视化支架有哪些？不同版本教材提供的直观模型有何相同与不同之处？笔者将人教版、浙教版、香港版以及美国加州版的教材进行了比较与分析。这四套教材安排的年段和单元名称如表1。

由表1可知，人教版、浙教版和美国加州版教材都把小数的初步认识安排在三年级下册，而香港版教材因把“小数的初步认识”和“小数的意义”安排在同一年级，所以放在了四年级下册。笔者对教材的具体素材和直观模型进行了比较，以选取有利于思维可视化的教学支架。

一、可视化素材比较

可视化素材是指教材的情境创设主题图和例题的直观模型。不同的素材有不同的教学路径和教学效果，四套教材的引入素材比较如下。

（一）情境创设的素材比较

人教版教材运用质量、价格、体温、身高等生活情境引入小数，浙教版教材运用水果的价格引入小数，香港版教材运用观看天气预报的生活场景引入小数，美国加州版教材是通过复习分数和美元的知识引入小数。

可见，四套教材都用学生已有的生活经验和知识引入小数，不同之处是各版本教材创设的引入情境类别不同。人教版、浙教版和香港版教材均采用生活中常见的小数，运用学生已有的生活经验引入，属于现实情境类别。美国加州版教材则运用学生已有的分数和货币知识经验引入，属于纯数学情境类别。

（二）例题的素材比较

解读这些教材发现，四个版本的教材都注重提供直观可视化素材，这是它们的相同之处。不同之处在于：

1.四套教材建构意义所选用的模型不同。人教版教材的例题采用“量身高”的具体情境结合米制系统建构小数意义;浙教版和香港版教材的例题均采用元和角的单位转化结合面积测量建构小数意义;美国加州版教材运用分数和小数的关系结合面积测量建构小数意义。

2.四套教材采用的例题数量不同。人教版和美国加州版教材只用1个素材作例题。人教版教材用“量身高”的现实情境虽然能使学生感受到小数的产生，但直接呈现半抽象的数线模型对三年级学生而言稍显困难。美国加州版只用小数是十进分数的1个面积模型素材略显单调。相比之下，浙教版和香港版教材都有2个例题素材，先用货币系统转化单位初次认识小数，再用面积测量建构小数意义。

3.归纳意义时所举例子方式不同。归纳一位小数的意义时，人教版和香港版教材是同一单位（米和分米或元和角）举例子后进行归纳的，相比之下，浙教版教材的处理就比较细腻，同一单位举若干个例子后，延伸到对不同单位“0.7米、0.7平方米、0.7吨”的理解，最后把小数的意义推广到不带单位的一般小数。

4.教学带小数意义的素材不同。众所周知，带小数的意义是这节课的难点。人教版教材只有 “1米3分米可以写成（  ）米” 一句话，这里的教学需要教师自己组织。浙教版和香港版教材则都呈现面积图突破带小数意义的理解，美国加州版教材小数的初步认识没有出现带小数。

二、可视化支架比较

从情境创设到习题安排，四套教材分别编排了哪些直观或半直观模型呢？见表3。

四套教材均采用了二维的面积模型作为思维可视化的支架。人教版教材呈现在习题中，浙教版、香港版和美国加州版教材在例题和习题中均有呈现。研读教材发现面积模型呈现频率最高，人教版和浙教版教材中面积模型各呈现了2次，美国加州版教材呈现了5次，在香港版教材中面积模型呈现了7次。

不同之处是思维可视化支架呈现的顺序不同。人教版教材是先选用米制模型作例题，结合半抽象数线模型进行小数意义建构，再将人民币实物模型、面积模型、数尺模型、数线模型当作练习呈现。浙教版教材是先选用货币实物模型建构一位小数的意义，再用面积模型建构两位小数的意义。香港版教材则先选用货币模型当例题，再结合面积直观模型建构小数意义，在后续学习中再呈现米制模型与数线模型。美国加州版教材则没有具体情境，直接用分数的意义结合面积模型建构小数意义。

三、教学启示：选取有利支架

通过对四种版本教材具体情境素材和可视化直观支架的比较与分析，笔者认为在具体教学中可从四个维度来选取有利支架，让思维可视化，从而促进小数意义的建构。

（一）情境支架——现实情境

杜威曾指出，由生活经验向科学概念的运动过程就是教学。教学小数的初步认识时可采用现实情境主题图引入，在读图时唤醒学生已有的生活经验，感受数学源于生活，激发学生的学习兴趣。这样的教学贴合学生的生活经验。在用现实情境引入小数时，可采用多种小数类型（纯一位小数，带一位小数，纯两位小数，带两位小数，小数末尾有0等），这一点人教版教材编排得比较周到。如果再增加一个比较大的小数则更好，如“我国最高的山峰珠穆朗玛峰海拔8844.43米”等，不仅能让学生知道小数其实并不小，还能让学生开阔视野，激发学习的兴趣。

（二）建构支架——货币模型、面积模型

人教版一年级的教材中编排了“元角分”，学生已经认识人民币及元角分单位间的转化，其他教材亦是在此前已经安排了“元角分”的认识。不仅如此，学生在平时生活中对人民币模型已积累了一定的生活经验，为学习小数的初步认识奠定了一定的基础。因此，对于三、四年级学生而言，他们对人民币模型的经验远多于米制模型的经验。为了让学生的生活经验在概念学习中发挥作用，笔者认为运用人民币模型，对建构小数的意义比较合适。

面积模型是学生具象思维走向抽象思维的有效桥梁。十等分的面积模型能很好地体现小数是特殊的十进分数这一本质，百方格的面积模型比数线模型能更直观地表示两位小数。

（三）衔接支架——米制模型、数线模型

教学中运用人民币模型后再運用米制模型进一步建构小数的意义。人民币模型涉及离散的量，而数学中的数是稠密的。教学时运用米和分米的单位转化结合半抽象的数尺模型进行教学，把半抽象的数尺模型转化成抽象的数线模型，扩充学生对数的认识。米制模型结合数线模型能与后续知识“小数的意义”的学习进行有效衔接。

（四）内化支架——动手操作、多元表征

图式是教材选用的支架，同时也是学生进行表征的支架。在用人民币结合面积模型初次建构一位小数的意义后，教师可以选择恰当的素材让学生运用新学知识动手操作。比如“0.7元、0.7米、0.7平方米、0.7吨”各表示什么意义？请学生选择其中一个用画一画或说一说等形式表示。有的学生用实物模型圈一圈，有的学生用面积模型画一画，有的学生用数线模型标一标，有的学生用文字写一写等，教学时让学生动手操作，以多元表征使学生更好地理解和内化知识。

参考文献：

[1]葛素儿，张君霞.基于图式的分数基本性质教学研究[M].北京：知识产权出版社，2019.

（浙江省杭州市富阳区富春第二小学   311400）