考虑船舶粘性阻尼的海缆敷设及登陆分析

姚兴隆，迟 岩，韩毅平，曹淑刚,2，梁 鹏

(1.中能电力科技开发有限公司 海上风电工程技术研究室，北京 100034； 2.华北电力大学 能源动力与机械工程学院，北京 102206； 3.中海石油有限公司天津分公司 渤海石油研究院，天津 300452)

0 引 言

高压海缆敷设施工成本高，技术难度大。准确分析海缆敷设过程的受力状态与运动响应是提高敷设质量与效率的关键关节，国内外学者为此开展了大量研究。胡玉娇等利用有限元法获取了海缆敷设过程中拉力作用下各层的机械特性[1]；陈然等建立了整体耦合模型，指出航行敷设时海缆张力的控制重点在于控制入水角[2]；Leclair等开展了海缆敷设动力学分析，指出弯曲刚度对海缆敷设时的张力及曲率影响较大[3]；卢青叶等采用ANSYS建立海缆的三维有限无模型分析了不同螺旋角度与不同摩擦因数对海缆弯曲刚度的影响[4]。

上述研究成果为高压海缆敷设提供了有力参考，但仍存在一些尚未解决的问题：(1)目前国内外均缺乏对海缆登陆的研究。由于海缆登陆工况复杂，对海缆张力、偏移和曲率的要求较高，开展登陆分析对海缆安全敷设至关重要。(2)目前国内外在开展敷缆船-高压海缆-系泊系统一体化耦合分析时往往忽略了敷缆船的粘性阻尼，导致敷缆船的运动响应结果偏大，影响了海缆力学分析的精确性。

为了填补高压海缆登陆的研究空白并提高耦合分析的精确程度，本文建立了高压海缆张力分布模型，在施加敷缆船粘性阻尼的情况下进行了敷缆船-高压海缆-系泊系统一体化耦合分析，开展了不同风浪流条件下海缆敷设受力及运动特性研究，并分析了海缆放缆状态与牵引登陆时粘性阻尼对海缆偏移、张力及曲率的影响。

1 高压海缆张力分布模型

海缆敷设时微元段受力如图1所示。由于海缆敷设时速度较慢，且海缆位形比较稳定，可近似取静态平衡状态对其进行分析[5]，其在切向及法向均满足平衡条件：

式中：T为第i节点处的高压海缆张力；dT为高压海缆相邻两个节点张力的差；T+dT为第i+1节点处的海缆张力；θ为高压海缆节点倾角；Δθ为高压海缆相邻两个节点倾角的差；Dt为切向高压海缆流体阻力；ΔS为高压海缆微元弧长；ω为高压海缆单位长度重量；Dn为法向高压海缆流体阻力[6]。

如图所示，ΔX为微元段相邻节点水平距离；ΔY为微元段相邻节点垂向距离。当ΔS趋近于无限小时，sin(Δθ)≈Δθ，cos(Δθ)≈1，且由于流体阻力Dt/Dn≈0.02，Dt相对于Dn而言可以忽略不计[7]，则式(1)与式(2)可改写为

两式相除，得到高压海缆张力与节点倾角的关系：

将式(5)沿缆长积分，即得到高压海缆的张力分布表达式，进而能够求解得到高压海缆在敷设过程中的位形、弧长以及张力大小[8]。

2 考虑敷缆船粘性阻尼的船舶水动力系数

2.1 敷缆船模型建立

本文以某海缆敷设船为例，对海缆敷设过程进行分析。该船为钢质、单甲板和非自航的工程船舶，在尾部设有3层上层建筑，中部设海缆储存盘一个，用于存放海缆，首部设A字架一个，用于吊放埋设机。船舶相关参数如表1所示。利用SESAM/GeniE软件建立船舶的水动力模型，如图2所示。

表1 敷缆船参数

图2 船舶水动力模型

2.2 粘性阻尼计算

敷缆船的阻尼可分为两类：粘性和漩涡阻尼。目前，常用的水动力计算软件普遍采用三维势流理论计算浮体响应，无法计入粘性阻尼的影响，导致计算结果偏大，影响计算精度[9]。本文在计算敷缆船水动力系数时，通过添加粘性阻尼矩阵来考虑粘性阻尼的作用。粘性阻尼可以通过计算临界阻尼后取百分比得到，临界阻尼的计算公式为

式中：M为敷缆船的质量或惯性矩；Ma为敷缆船的附加质量；Ci为敷缆船的静水回复刚度。

敷缆船临界阻尼的计算结果如表2所示。由于纵荡、横荡和艏揺3个水平方向的运动受系泊系统影响较大，故本文仅计算敷缆船的垂荡、横摇和纵摇临界阻尼[10]。

表2 敷缆船临界阻尼的计算结果

敷缆船粘性阻尼通常为临界阻尼的2%～10%，本文计算时取7%，垂荡、横摇和纵摇的阻尼比如表3所示。

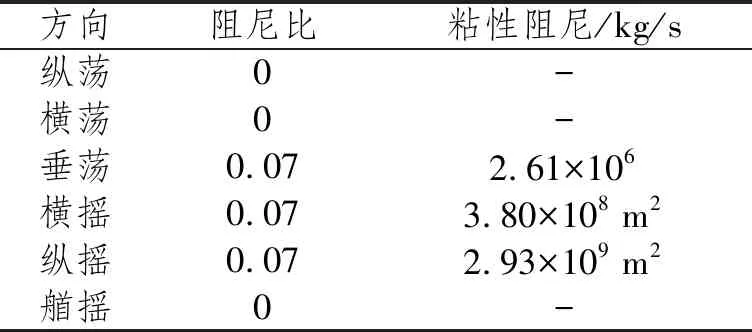
表3 阻尼比与粘性阻尼

2.3 粘性阻尼的影响分析

本文通过SESAM/HydroD软件分析海缆敷设船的响应幅值算子[11](Response Amplitude Operator，RAO)。由于纵摇和横摇两方向自由度的运动对海缆敷设及海缆登陆的受力及运动的影响十分有限，故本节只分析敷缆船粘性阻尼对垂荡运动RAO的影响。

分析时以某海上风电场海缆敷设工程为例，该工程海域水深介于0～30 m范围内，因此选取30 m水深作为分析条件。图3给出了船体垂荡运动RAO分析结果。由图可知，忽略船体的粘性阻尼，在入射波角度为75°，波浪周期6 s左右时，船体的垂荡幅值最大达到了2.22 m。考虑粘性阻尼时，船体的垂荡幅值最大不超过1 m，幅值仅为原来的45%。可见粘性阻尼对船体的垂荡幅值有明显影响，若忽略粘性阻尼计算结果将会产生很大偏差。

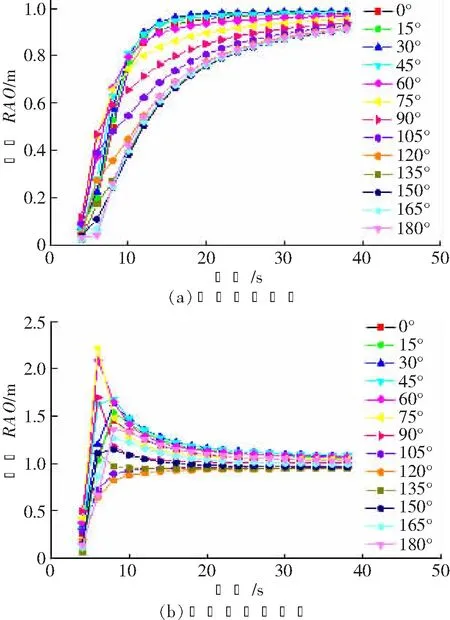
图3 船体垂荡RAO

海缆敷设过程中，船体的运动(垂荡运动)是影响海缆受力的最重要因素之一，船体的垂荡运动响应偏大会使海缆受力的计算结果过于保守，进而影响海缆的敷设施工。

3 海缆敷设状态响应分析

由以上分析可知，粘性阻尼对船舶运动影响较大，进而影响海缆敷设过程的受力及曲率，本节将具体分析敷缆船-高压海缆-系泊系统一体化耦合状态下考虑及不考虑粘性阻尼时海缆的张力及曲率情况，敷设海缆的参数如表4所示。

表4 海缆参数

海缆敷设时线型可看作为悬链线，本文分析模型海缆触地点约在距敷缆船船尾水平距离118 m处。分析时选取JONSWAP波浪谱，波高为2.5 m，风速为6 m/s，流速为0.9 m/s。为了更为清晰地描述敷缆船粘性阻尼对海缆受力的影响，计算了风浪流同向、入射角分别为45、90、135和180°时的海缆曲率与有效张力，计算结果如图4及表5所示。

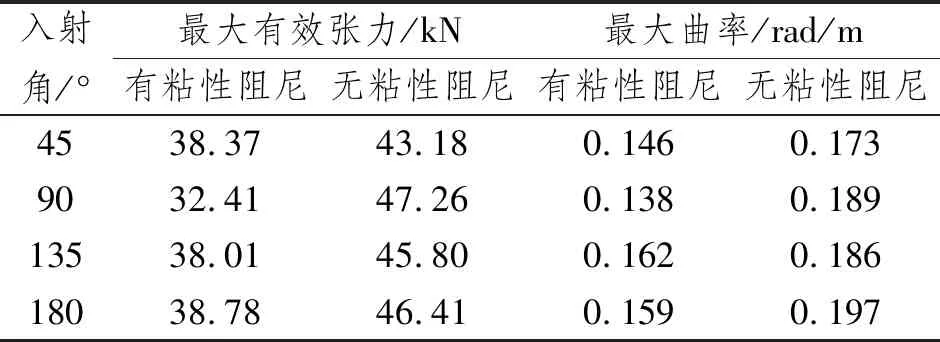
表5 海缆张力与曲率分析结果对比

图4中沿缆长递减的两条曲线为有效张力，沿缆长先增后减的曲线为曲率。由图可知，不考虑粘性阻尼的海缆最大张力及最大曲率均较考虑粘性阻尼时大，计算结果偏大会使海缆敷设施工的允许海况变小，降低敷设施工效率。

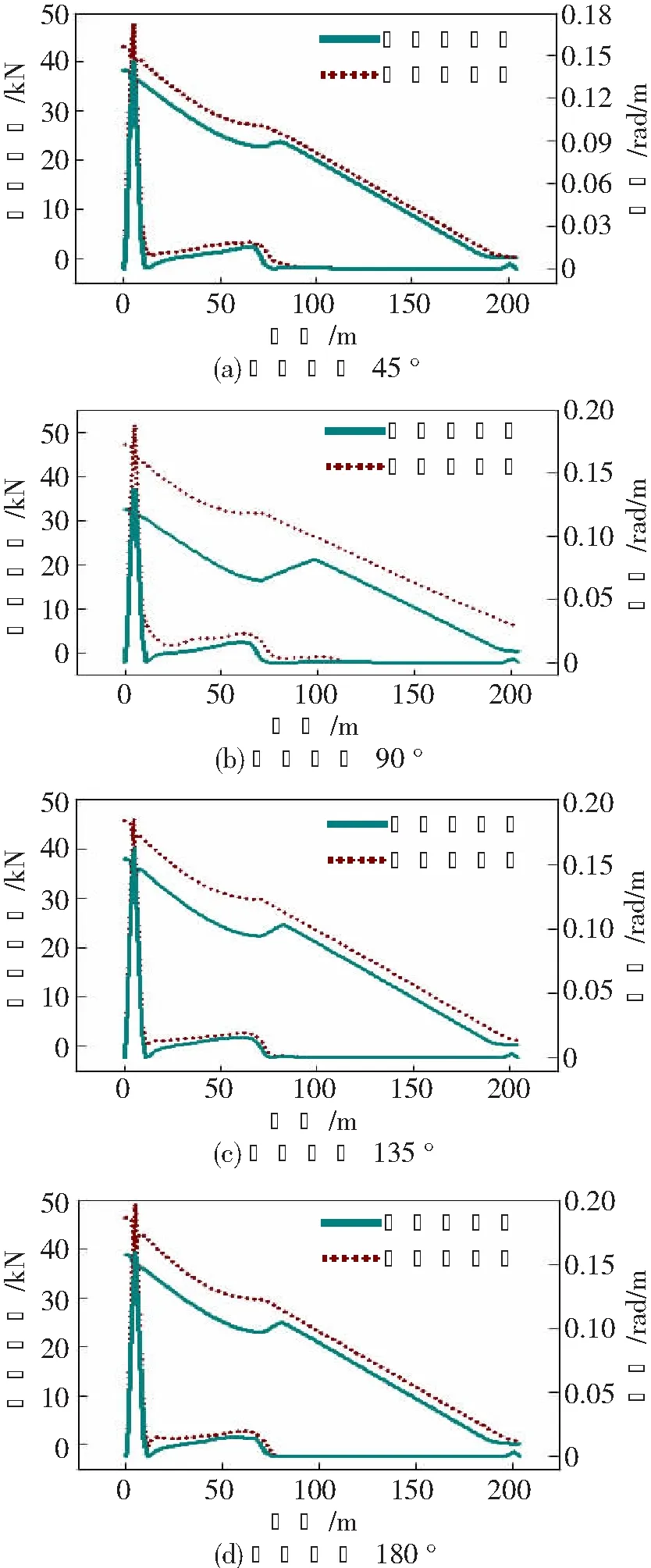
图4 海缆张力与曲率的分布

4 海缆登陆过程分析

4.1 分析模型的建立

海缆登陆是海缆敷设过程中最复杂和最易出现故障的关键节点。由于目前对海缆登陆分析不够重视，对海缆敷设允许作业海况缺乏科学指导，导致海缆敷设工程存在作业窗口期小、敷设效率低等缺点。本节将在考虑敷缆船粘性阻尼的情况下对海缆登陆过程进行分析，进而给出海缆登陆允许作业海况以供工程参考，达到增加作业窗口期、提高海缆敷设效率的目的。

考虑到海缆的登陆作业极易受海域征迁面积的影响，因此，本节针对特定海缆敷设工程的登陆过程对海缆运动状态和受力情况进行分析。

利用Orcaflex软件建立海缆登陆模型，海缆末端的边界条件分别设置为自由漂浮和铰接模拟登陆过程中的放缆及牵引两个阶段。本文中敷缆船在离岸280 m处放缆，海缆登陆时的锚泊布置方案如图5所示。

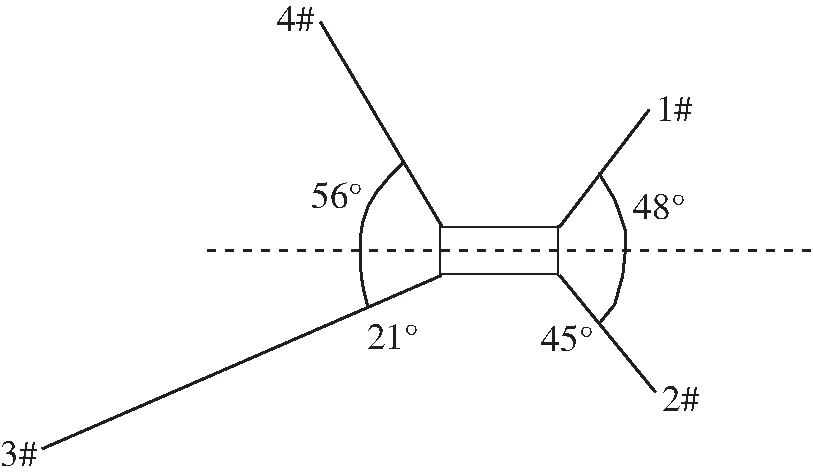
图5 海缆登陆时锚泊布置方案

在Orcaflex软件中建立了敷缆船-高压海缆-系泊系统耦合模型，模型如图6所示。

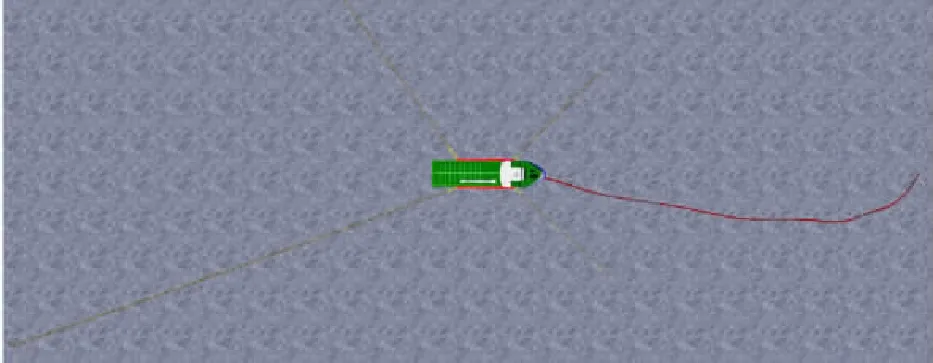
图6 耦合模型

海缆始端登陆时通常通过绑扎助浮装置的方式来使海缆浮于海平面，如图7所示。本章在采用Orcaflex软件进行海缆登陆分析时，采用配置浮力块的方式进行模拟，分析时将每个浮子的浮力和拖曳力等均匀地分布在从浮心前Sf/2到浮心后Sf/2的海缆长度上，Sf为浮心间距。等效后的海缆与浮力块模型外径为0.5 m、长度为1.0 m,且各浮力块紧靠，单位体积质量为0.35 t/m3，原海缆的拖曳力系数为1.20，等效后拖曳力系数变为3.32，轴向刚度及弯曲刚度不变，与原海缆模型相同。

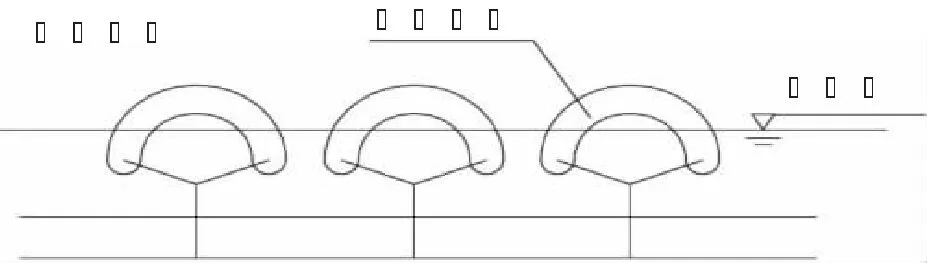
图7 海缆助浮登陆

4.2 海缆放缆状态分析

海缆登陆时首先需放缆，随后用钢丝绳将其牵引至陆上，放缆时海缆端部为自由漂浮状态，该状态下海缆极易因偏移过大而超出征迁区。海缆敷设所在海域征迁区外往往养殖区密布，海缆偏移进入养殖区极易造成养殖区破坏或海缆损毁的严重后果。本节通过对敷缆船-高压海缆-系泊系统一体化耦合的分析，研究海缆在征迁区内作业时的运动状态，进而给出最大可作业海况，为海缆的敷设工程提供参考。分析时考虑了敷缆船的粘性阻尼，避免了因忽略敷缆船粘性阻尼导致的最大可作业海况偏保守的缺陷。

本节选取表6所示的9个典型工况开展讨论。图8和9所示分别为不考虑及考虑粘性阻尼时海缆的偏移量、有效张力以及曲率。本文依托工程的征迁区域宽度为280 m，敷设时敷缆船位于征迁区的中部，图8(a)中偏移量为-140 m处的水平虚线即表示该海域的征迁边界。

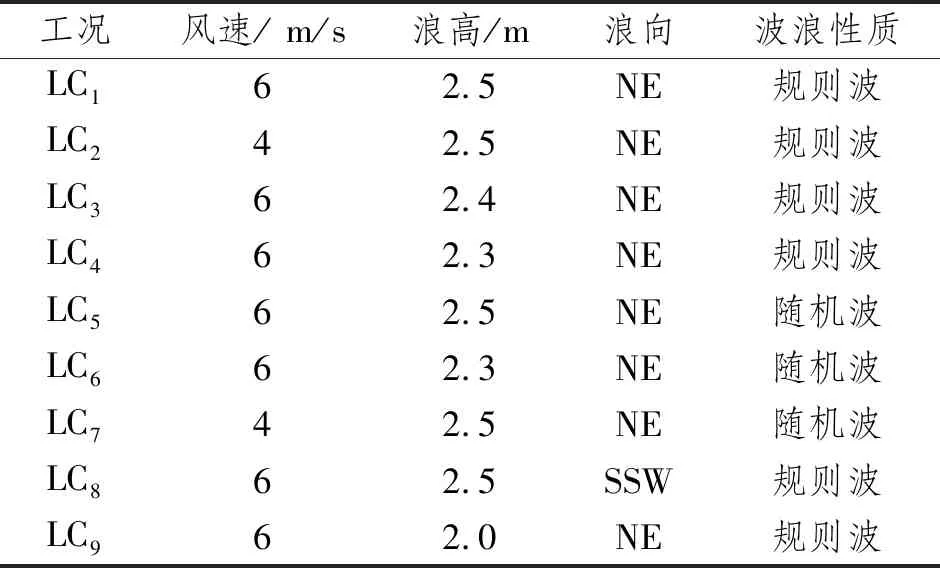
表6 计算工况

注：NE为东北；SSW为西南偏南。

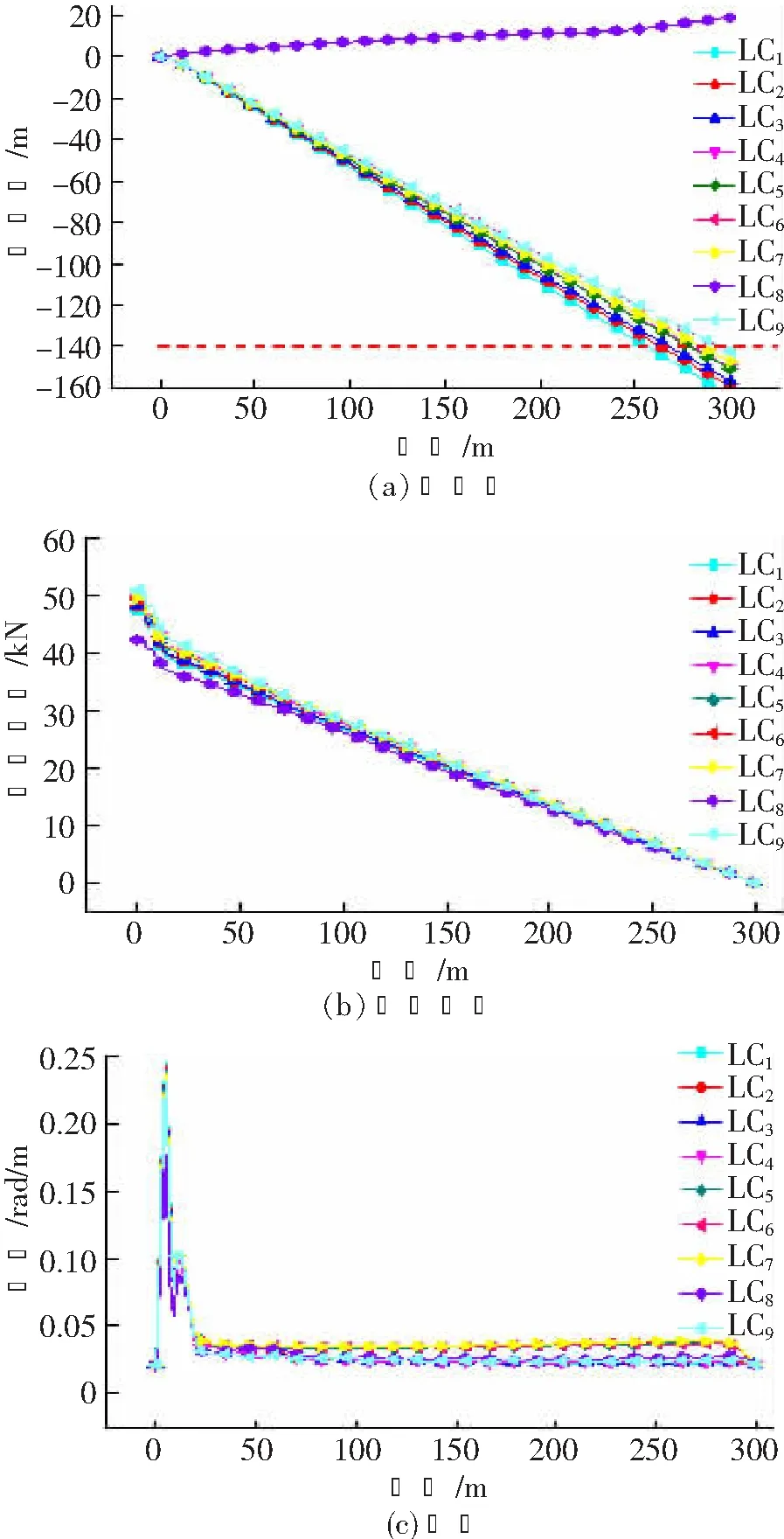
图8 不考虑粘性阻尼时海缆偏移量、有效张力及曲率

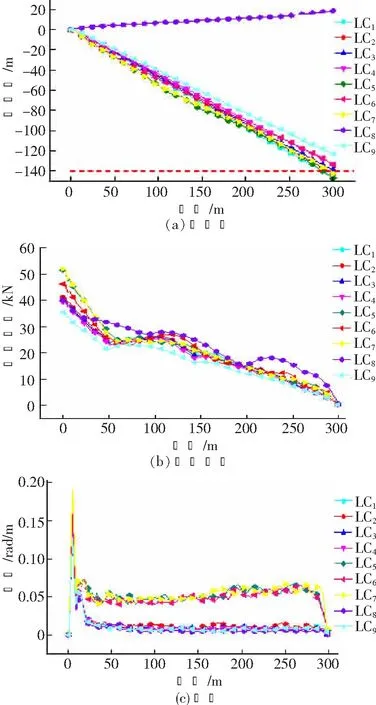
图9 考虑粘性阻尼时海缆偏移量、有效张力及曲率

由图分析可知：

(1) 海缆敷设的最大允许作业海况主要受偏移量大小的影响，在偏移量超出边界时的海况作用下，有效张力与曲率仍不超过允许值。

(2) 次常浪向时，风、浪和流的作用方向分别为NE、SSW和西北偏西(West-Northwest,WNW)，风浪流的作用效果相互抑制，海缆的末端偏移量较小。

(3) 海缆的最大有效张力位于张紧器处，最大曲率位于拖缆架处。有效张力沿缆长方向逐渐减小，由于此工况海缆末端为自由漂浮状态，因此末端张力为0。

(4) 考虑粘性阻尼后，海缆的偏移量变小，考虑粘性阻尼进行海缆敷设分析会提高敷设施工的允许作业海况，进而提高施工效率。

(5) 由图8(b)与图8(c)和图9(b)与图9(c)可知,考虑粘性阻尼后，虽然部分节点的张力与曲率变大，但海缆的最大有效张力与最大曲率会变小。

(6) 考虑粘性阻尼时，当浪高超过2.4 m、风速超过6 m/s时，海缆的最大偏移将超出征迁区边界，该海况即为分析所得最大允许海况，海缆登陆时可参考该极限海况进行海缆的敷设施工作业。

为分析船舶粘性阻尼对海缆登陆的影响，计算了不考虑船舶阻尼时海缆登陆时的偏移量。表7所示为最大偏移量分析结果，其分别给出了考虑和不考虑敷缆船的粘性阻尼时海缆最大偏移的数值分析结果。当浪高2 m、风速6 m/s时，不考虑船舶粘性阻尼的海缆末端偏移就已超过征迁边界，因此不考虑船舶粘性阻尼时海缆登陆允许作业海况明显比考虑船舶粘性阻尼时确定的允许作业海况(浪高2.4 m)小，故不考虑船舶粘性阻尼的分析方法将会缩短海缆登陆的作业窗口期，影响海缆敷设的施工效率。

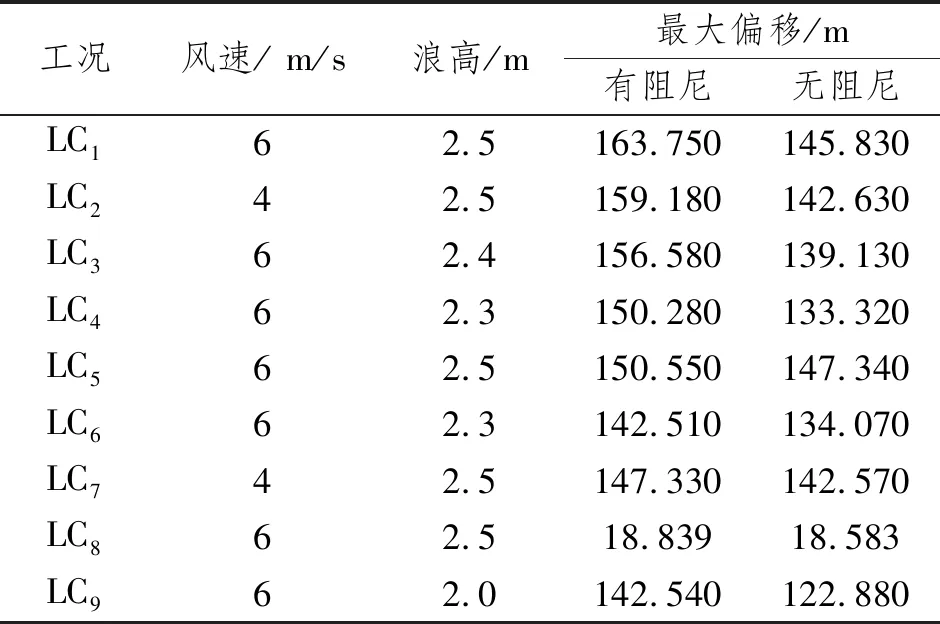
表7 最大偏移量分析结果

4.3 海缆牵引登陆分析

本节研究了在海缆登陆过程中，考虑粘性阻尼时，末端由钢丝绳牵引登陆时的海缆偏移量、有效张力以及曲率的特性。数值分析结果如图10所示。

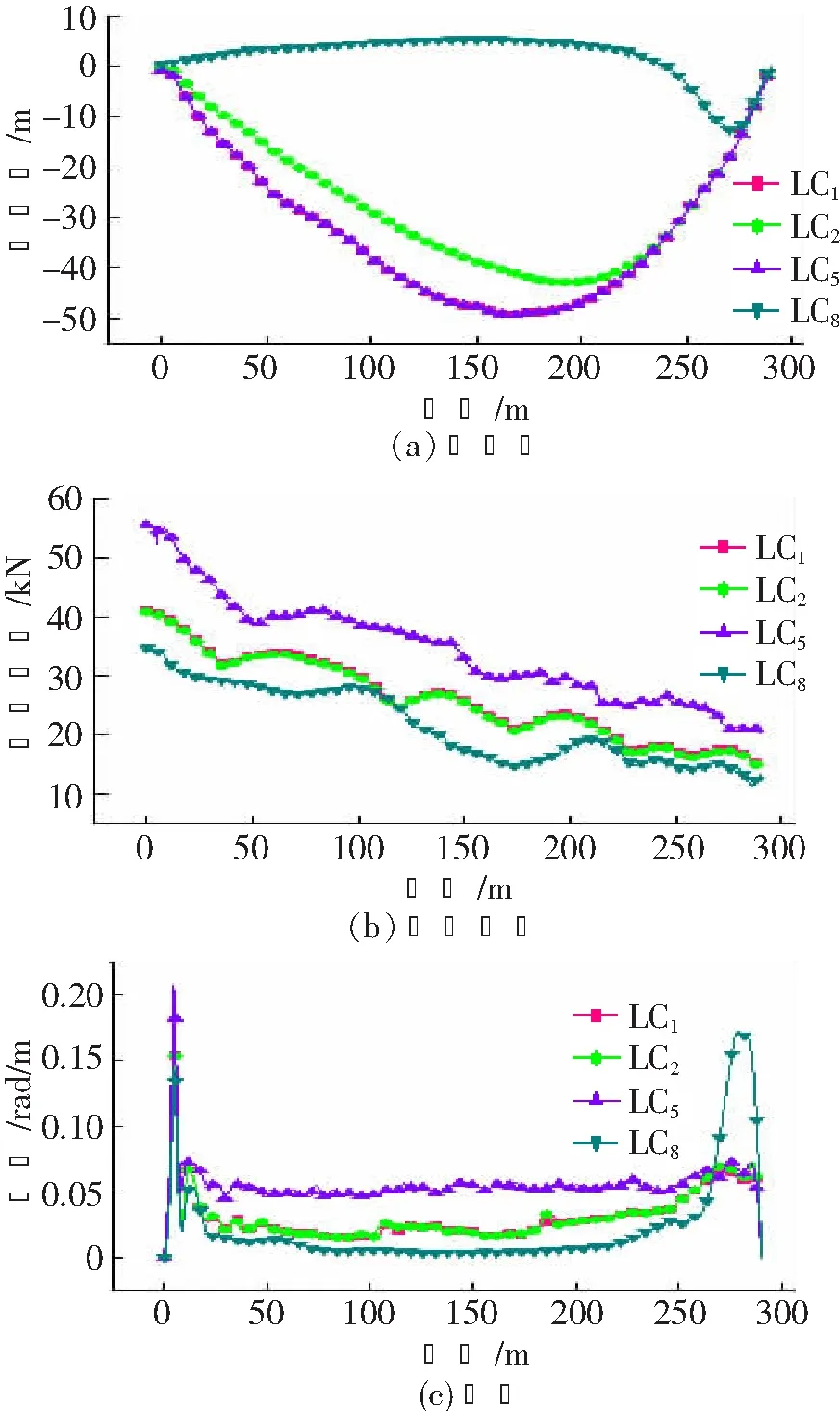
图10 末端铰接、考虑粘性阻尼时的海缆偏移量、有效张力及曲率

由图可知，海缆在端部牵引登陆时具有以下特性：

(1) 当波浪方向为主常浪向时，海缆的最大偏移位于海缆中段，最大偏移量不超过50 m；当波浪方向为次常浪向时，由于风浪流的作用效果相互抑制，海缆偏移值较小。

(2) 当波浪方向为主常浪向NE时，海缆最大曲率位于拖缆架处，远离张紧器时海缆线型较为平顺；当波浪方向为次常浪向SSW时，海缆线型较为复杂，曲率沿缆长出现多个峰值。

5 结束语

目前国内外对敷缆船-高压海缆-系泊系统一体化耦合系统的研究重点集中于海缆的受力分析，

对敷缆船的水动力性能关注较少，往往忽略敷缆船的粘性阻尼，导致船舶运动响应结果存在偏差，进而影响海缆动力响应分析和力学性能分析的精确程度。本文在SESAM/HydroD软件中分析了考虑粘性阻尼的敷缆船运动RAO，在Orcaflex软件中建立敷缆船-高压海缆-系泊系统一体化耦合模型分析了船舶粘性阻尼对耦合系统的影响。分析结果表明，考虑粘性阻尼后船体的垂荡幅值减小约55%，海缆敷设时的有效张力、曲率及海缆登陆时的偏移量均明显减小。对耦合模型施加船舶粘性阻尼将提高海缆动力响应分析及受力分析的精确性，使耦合分析结果更具参考价值。

高压海缆登陆是海缆敷设过程中最关键、最复杂和最易出现故障的关键节点，目前国内外对海缆登陆过程的研究极少。本文利用Orcaflex软件建立海缆登陆模型，在考虑敷缆船粘性阻尼的情况下研究海缆登陆过程，给出了海缆登陆允许作业海况。研究结果表明，考虑船舶粘性阻尼，当浪高超过2.4 m、风速超过6 m/s时，海缆的最大偏移将超出征迁区边界，以考虑船舶粘性阻尼的分析结果作为工程指导可有效减少海缆登陆海域的征迁面积，增加作业窗口期。

然而，本文仅开展了海缆的始端登陆过程研究，并未分析海缆的末端登陆，由于海缆末端登陆时缆形为“倒U形”，对海缆曲率的要求较始端登陆高，因此有必要针对海缆末端登陆曲率控制开展深入分析。此外，耦合模型锚泊布置方案的变化、触地点的缆-土相互作用及海缆参数变化对海缆敷设与海缆登陆的影响本文并未涉及，因此更完善的海缆敷设与登陆分析有待今后进一步研究。