一种改进的分数阶双线性数字预失真方法

王 恒，徐方雨

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

为了充分利用频谱资源，目前现代通信系统广泛采用非恒定包络的调制方式[1]，而该调制方式对射频功放的性能提出了更高的要求[2-3]。在实际应用中，一方面，为了提高功放的效率，往往会使其工作在临近饱和区，此时功放的输入输出不是线性关系；另一方面，由于信号带宽增大，功放将会表现出强记忆效应。因此，功放的非线性记忆效应会影响信息的正确传输，导致带内失真和带外频谱扩展[4]。

在现有线性化技术中，数字预失真技术使用最广泛[5-6]。目前常用的数字预失真模型有：Volterra级数、记忆多项式(Memory Polynomial，MP)、广义记忆多项式(Genneral Memory Polynomial，GMP)、分数阶记忆多项式(Fractional Order Memory Polynomial，FMP)和传统的双线性多项式模型等。Volterra级数[7]有很好的建模能力，但运算量比较大；MP模型是Volterra级数的简化形式[7]，只包含Volterra级数矩阵主对角线上的参数，简化了模型复杂度，但建模误差较大；GMP模型[8]虽然考虑了功放的记忆效应，但由于交叉的引入导致了运算量过大；FMP模型[9]虽说在建模能力上有了提高，但对于强动态非线性的建模能力仍然有限；传统的双线性多项式模型引入了反馈项，但不能表征高阶非线性特性。针对现有研究中存在的问题，本文提出了一种改进的分数阶双线性多项式模型。

1 改进的分数阶双线性多项式模型描述

最常用的数字预失真模型大多数为MP模型，因为该类模型能够很好地表征射频功率放大器的非线性记忆效应，许多文献提出的模型都是基于MP模型。其中，FMP模型也是在常用MP模型的基础上进行改进的，由于功放偶数阶次项带来的非线性失真不明显，所以可将偶数阶次改为分数阶次来提高对非线性失真的抑制能力，但对功放的强记忆效应并没有很大的改善。传统的双线性多项式模型同样也是在MP模型的基础上进行的改进，与MP模型不同的是，它将过去时刻的输出项和输入—输出交叉项引入一阶线性输入序列，是一种带有反馈结构的非线性系统模型，由于双线性多项式模型只能通过交叉项来表征系统的非线性，所以对高阶非线性特性的建模不够精确。

1.1 FMP模型

FMP模型的表达式为

式中：x(n)和y(n)分别为该模型的输入和输出信号；k为该模型的非线性阶数，k∈[0,K],K为k的最大整数值；q为该模型的记忆深度，q∈[0，Q]，Q为q的最大整数值；akq为该模型的系数；mod(k,2)为k对2的取模运算。

1.2 传统的双线性多项式模型

传统的双线性多项式[10]模型的表达式为

式中：cj为该模型输出项的系数；ai为该模型输入项的系数；bij为该模型反馈交叉项的系数；i为该模型输入项的记忆深度，i∈[0，Q]；j为该模型输出项的记忆深度，j∈[0，K]；N1和N2为该模型反馈交叉项的记忆深度。表达式中第1和第3部分均表示反馈项，第2部分表示输入项。

1.3 改进的分数阶双线性多项式模型

FMP模型虽然在建模能力上有一定的提高，但对功放的强记忆效应不能很好的建模；传统的双线性多项式模型仅仅是一个一维模型，其只有纯粹的输入输出数据，其非线性特点只能通过交叉项来进行表征，对系统的高阶非线性建模精确度不高。本文采用传统的双线性多项式模型的反馈解决问题思路，结合FMP模型的优点，提出一种改进的分数阶双线性多项式模型，该模型兼顾了以上两种模型的优点，显著降低了模型系数数量，提高了建模的精确度，同时也能更好地表征功放的非线性特性和强记忆效应特性。

改进的分数阶双线性多项式模型的表达式为

式中：akxqx为该模型输入项系数；akzqz为该模型输出项系数；kz和qz分别为该模型输出项的非线性阶数和记忆深度，且kz∈[1，Kz]，qz∈[1，Qz]，Kx和Qz分别为kz和qz的最大整数值；kx和qx分别为该模型输入项的非线性阶数和记忆深度，且kx∈[0，Kx]，qx∈[0，Qx]，Kx和Qx分别为kx和qx的最大整数值。

2 系统辨识结构及迭代算法

2.1 系统辨识结构

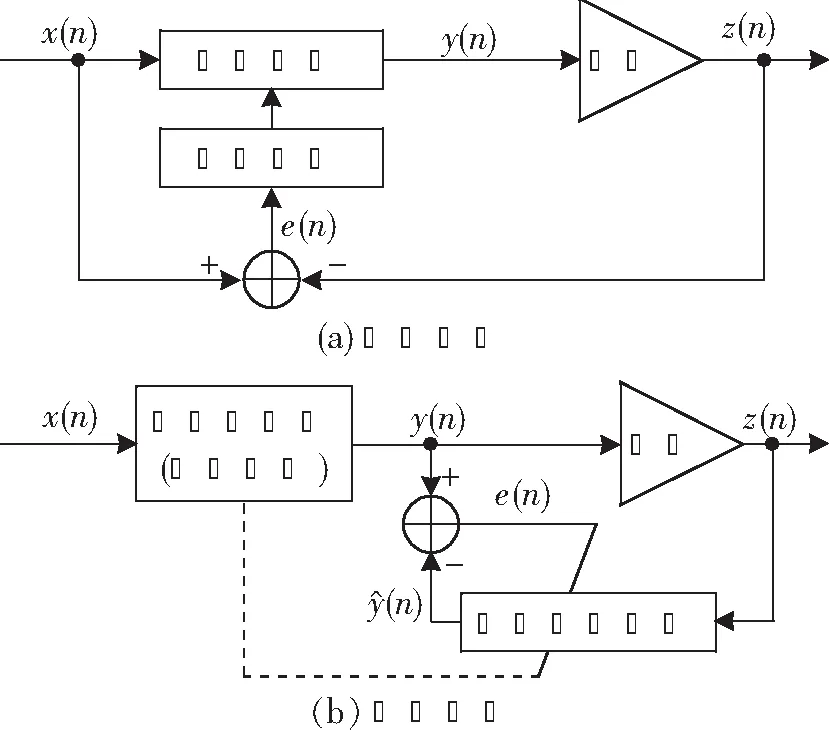
图1 系统辨识结构示意图

在实际的工程应用中，由于并不知道功放具体的行为模型，只是假设在结构上存在一个与预失真器完全一样的后预失真器，所以通过分析直接学习和间接学习结构各自的特点，本文采用间接学习结构进行系统模型参数辨识。

2.2 系统辨识算法

用于系统自适应辨识的算法有很多种，但是最常用的有最小二乘 (Least Square，LS)、最小均方 (Least Mean Square，LMS)和递推最小二乘(Recursive Least Square，RLS)算法。

(1) LS算法

LS算法是一种实用算法，它是通过求实际值与模型计算值之差的平方和达到最小值作为最小二乘法的解[13]。

(2) LMS算法

LMS算法以计算复杂度较低、性能较稳定和硬件实现相对较简单等优点而被广泛应用于各种自适应辨识系统算法中[14]。LMS算法的思想主要是利用随机梯度下降法来使代价函数最小化。

(3) RLS算法

通过与LS及LMS算法对比可知，LS算法系统辨识算法是最简单的，但在算法求解的过程中需要进行矩阵求逆，而矩阵求逆过程比较复杂，需要消耗大量的时间且求解相当困难；LMS算法虽然计算量较小，但收敛速度较慢，且会受到收敛步长的限制导致收敛精度不高；而RLS算法虽然迭代时的计算量加大，但无论在收敛速度还是收敛精度上效果都比较好，所以综合考虑，本文将RLS算法辨识用于改进的分数阶双线性模型的仿真验证中，该算法具体的推导过程如下：

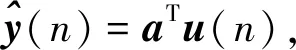
RLS算法是通过n-1时刻的数据去估计n时刻的数据并经过多次迭代得到的，有关RLS算法详细的推导过程见文献[15]，最终的迭代过程和公式如下：

3 仿真分析与验证

3.1 模型评价

评价模型精度的标准有很多种，本文使用归一化均方误差(Normalized Mean Square Error，NMSE)来衡量所建模型的精度。NMSE的表达式[16]为

式中：NMSE单位为dB，其能很好地反映模型与实际模块的接近程度，其值越小越好；y(n)为实际测试得到的模型输出信号；ymodel(n)为模型计算的输出信号；N为样本的数量。

3.2 仿真结果分析

为了验证以上所提方案的合理性，本文通过Matlab 2018a软件产生大量的正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)信号进行验证分析。考虑到数据量过大，本文截取了其中4 096组数据进行仿真分析，将所截取的带宽为1.85 MHz的信号作为系统输入信号，采用间接学习结构并结合RLS算法实现预失真参数提取。选取输入输出信号的幅度-幅度 (Amplitude Modulation to Amplitude Modulation Effects, AM-AM)曲线、幅度-相位(Amplitude Modulation to Phase Modulation Effects, AM-PM)曲线、NMSE、邻道功率泄露比(Adjacent Channel Power Ratio，ACPR)等指标进行验证分析。

(1) AM-AM、AM-PM曲线

AM-AM和AM-PM曲线是用来反映功放非线性记忆效应特性的表现形式，对于理想的线性系统来说，其AM-AM曲线发散程度比较小，近似为一条比较理想的直线，AM-PM曲线同样也是一条近似为零的直线[17]。

系统在未进行预失真处理的情况下，功放输出的AM-AM与AM-PM曲线如图2所示。

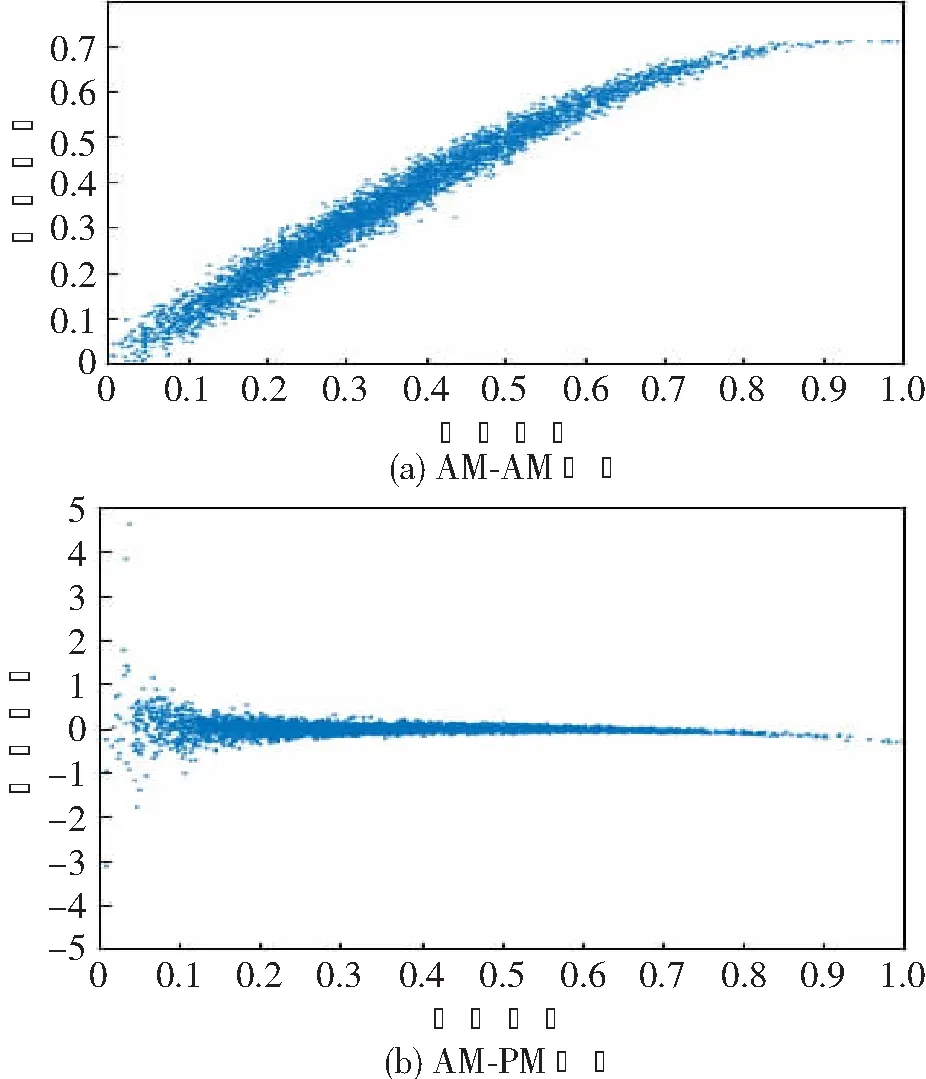
图2 预失真处理前的曲线图

由图2(a)可知，预失真处理前功放输出的AM-AM曲线是一条较发散的曲线，且非线性关系，其输出信号的幅度随着输入信号幅度的增加将会达到饱和状态，即输出信号幅度的增加速度越来越慢。在实际工程应用中，为了提高功放的效率，一般会使功放工作在临近饱和区。

由图2(b)可知，预失真处理前功放输出的AM-PM曲线是一条近似为零的曲线，功放在小信号输入的情况下，输入信号受之前输入信号的影响较大，所以曲线较发散，这也更进一步表明了功放的记忆效应较明显；而在大信号输入的情况下，输入信号受之前输入信号的影响较小，曲线的发散程度也较小。

经过预失真处理之后功放输出的AM-AM与AM-PM曲线如图3所示。

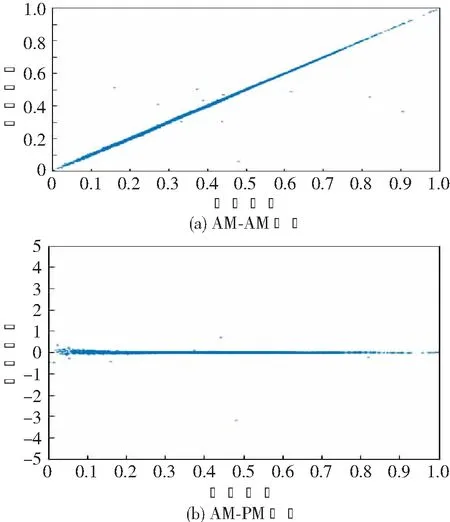
图3 预失真处理后的曲线图

由图可知，经预失真处理后功放输出的AM-AM和AM-PM曲线发散程度较小，近似为一条理想的直线。所以，经预失真处理后，功放的非线性记忆效应得到了很好的校正，使得系统更接近于理想的线性系统。

(2) NMSE参数

使用本文提到的数据结合改进的分数阶双线性多项式模型，并使用间接学习系统辨识结构，应用RLS自适应辨识算法进行建模分析。表1将本文提出的改进的分数阶双线性多项式模型分别与MP、GMP、FMP以及传统的双线性多项式模型在模型的参数设置、NMSE值和模型系数个数这3个方面进行比较，来验证建模的效果。

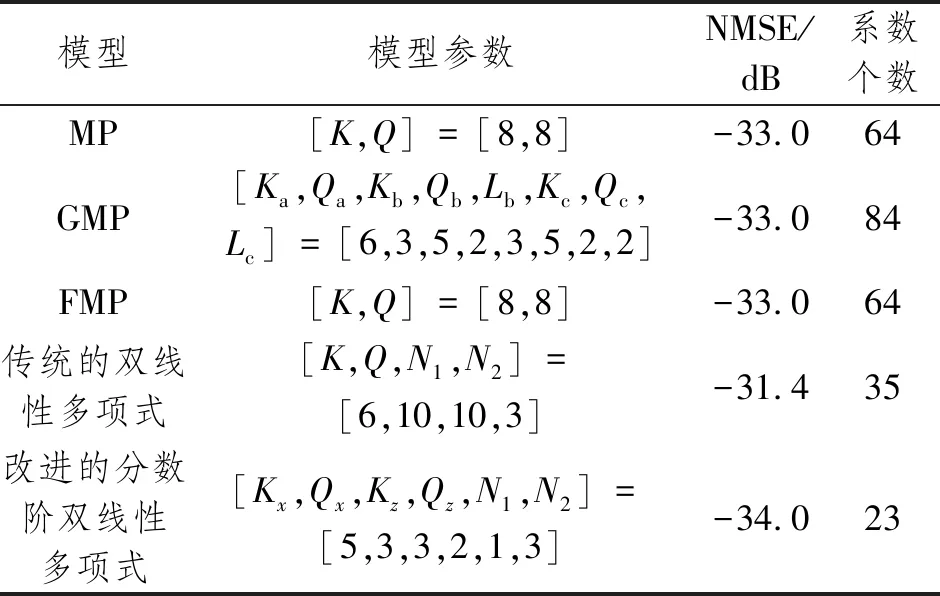
表1 不同模型性能比较

由表可知，改进的分数阶双线性多项式模型和其他几种多项式模型相比，NMSE值均有所提高，系数个数均比这几种多项式模型少，和传统的双线性多项式模型相比NMSE提高了2.6 dB，系数减少了34.3%。可见，本文提出的模型无论是在建模的精确度上还是在计算复杂度方面均有一定的改善。

实现功放线性化效果的目的之一是减小信号的带外频谱扩展，如果带外频谱扩展比较严重则会使信道内的信号功率泄漏到相邻信道，影响信号的传输效果。而衡量频谱扩展能力的指标为ACPR[18]，图4和5展示了原始信号、功放输出信号以及预失真处理后输出信号的功率谱密度图。

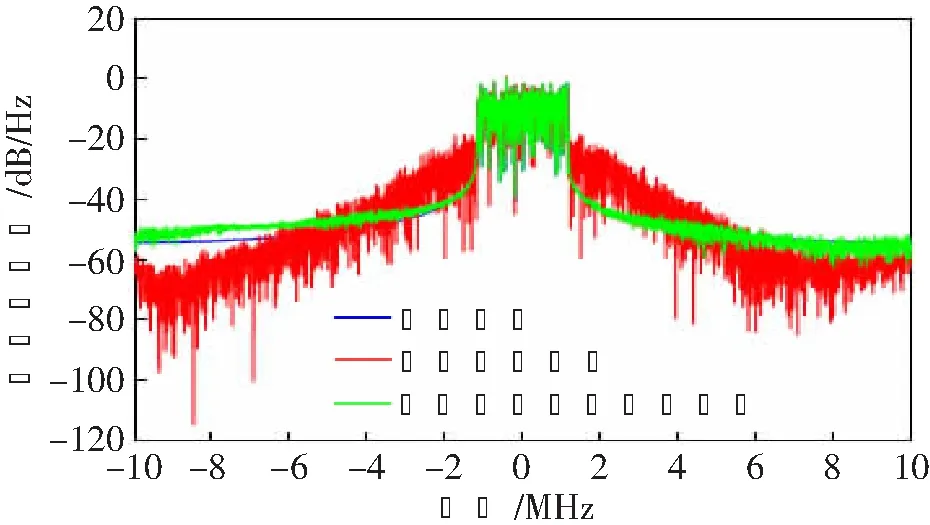
图4 预失真处理前后功率谱密度图

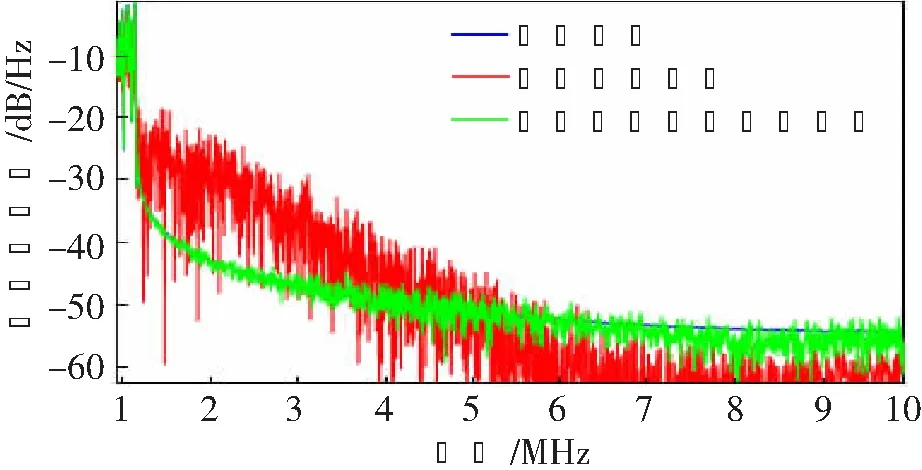
图5 预失真处理前后功率谱密度局部放大图

由图可知，系统未经预失真处理时对带外频谱扩展的抑制效果非常差，但在经过预失真处理后，功率谱更接近于输入信号的功率谱特性，明显比未经预失真处理时的效果好。所以，经预失真处理后，对功放的带外频谱扩展的抑制效果有了显著改善。

(3) ACPR

ACPR表征了系统的带外频谱扩展能力。表2列出了几种不同模型在偏离载波上下2.35 MHz时的ACPR值。

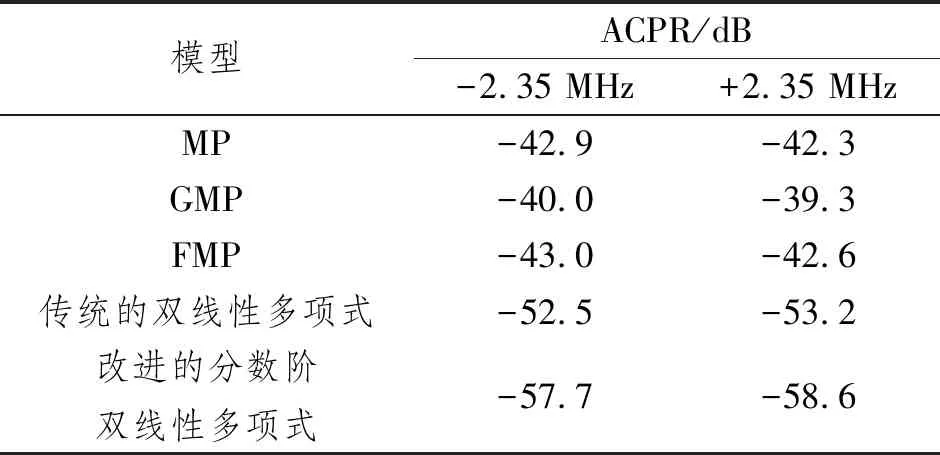
表2 不同模型在偏离载波上下

由表可知，改进的分数阶双线性多项式模型和其他几种多项式模型相比有较好的抑制带外频谱扩展的效果，其ACPR值均有一定的改善，与传统的双线性多项式模型相比，ACPR值改善了约5 dB。

4 结束语

本文介绍了几种常用的基于MP的预失真器模型，在FMP和传统的双线性多项式模型的基础上，提出了一种改进的分数阶双线性多项式模型，该模型采用了间接学习系统辨识结构和RLS自适应辨识算法提取预失真器的模型系数。实验结果表明，与传统的预失真模型相比，改进的分数阶双线性多项式模型减少了模型系数，降低了计算复杂度，能够更有效地改善功放的非线性记忆效应，使功放输出达到理想的线性化效果，具备良好的实际工程应用前景。