基于每层泊松近似的异构蜂窝网络性能分析

杜京城，杨 洁，周 健

(1.南京邮电大学 a.通信与信息工程学院; b.物联网学院，南京 210003； 2.南京工程学院 通信工程学院，南京 211167)

0 引 言

随着用户数量和移动数据流量的快速增长，蜂窝网络正趋于更高的数据速率和更复杂的异构性。异构蜂窝网络(Homogeneous Cellular Network, HCN)因其有着更高的效率而被提出并得到广泛关注[1]。

传统的基于网格模型的蜂窝网络建模得到的结果并不是十分的精确，且与实际基站部署也不太符合[2]。而基于随机几何的泊松点过程(Poisson Point Process，PPP)模型不仅很好地描述了网络集合拓扑的随机性，还提供了便于分析的结果[3-4]。然而实际基站部署并不是完全随机的，一方面， 基站之间存在排斥，可以使用泊松硬核过程(Poisson Hard-Core Processes, PHCP)建模[5]；另一方面，在文献[6]中，泊松簇过程(Poisson Cluster Processes, PCP)被证明可以准确地模拟许多城市的基站部署，特别是在较大的地理范围内，由于城市地区的高密度和农村地区的低密度，基站分布似乎形成了一个集群点过程。因此，研究非PPP蜂窝网络的性能非常重要。

文献[7-9]对非PPP进行了研究，指出一般性的单层网络覆盖率Pc(θ)P(SIR>θ)，P(SIR>θ)为信干比(Signal to Interference Ratio, SIR)大于给定泊松网络的SIR门限θ的概率，可以通过缩放θ到θ/G近似得到，即式中：为PPP的覆盖率；G为近似增益。G可以通过使用平均干扰信号比(Mean-Interference-to-Signal Ratio， MISR)来量化，因此被称为基于MISR的增益，此种方法称为泊松SIR近似方法(Approximate SIR Analysis based on PPP, ASAPPP)，它代表“基于PPP的近似SIR分析”。

本文将利用PHCP对HCN进行建模，并把单层ASAPPP扩展到两层基于PHCP的HCN中，从而获得可分析性较高的理论结果。

1 系统模型

定义：PHCP

记φp为密度为λp的PPP，图1(a)所示为PPP模拟的基站分布图。对于每个x∈φp，去除b(x,r)区域中的所有点，b(x,r)为以x为圆心、r为半径的一个圆，φp剩下的点构成的点过程称为PHCP，记作φPHCP。

筛选r=2时的φPHCP如图1(b)所示，筛选r=4时的φPHCP如图1(c)所示。

本文考虑两层HCN模型，微基站用PPP建模，考虑到宏基站之间的互斥性，宏基站用PHCP建模，两层之间相互独立。不失一般性,本文以位于原点的典型用户作为讨论对象并分析其性能。假设网络接入方式为开放式接入,即用户可以选择接入提供最大SIR的基站。路径损耗函数为l(R)=|R|-α，α>2，式中：α为路径损耗因子；R为典型用户与服务基站的距离。本文研究的网络假设为干扰受限系统，则典型接收机的干扰功率是典型用户接收到的来自于服务基站以外的所有其他基站接收功率的总和。假设典型用户接入第k层，则该典型用户的SIR为

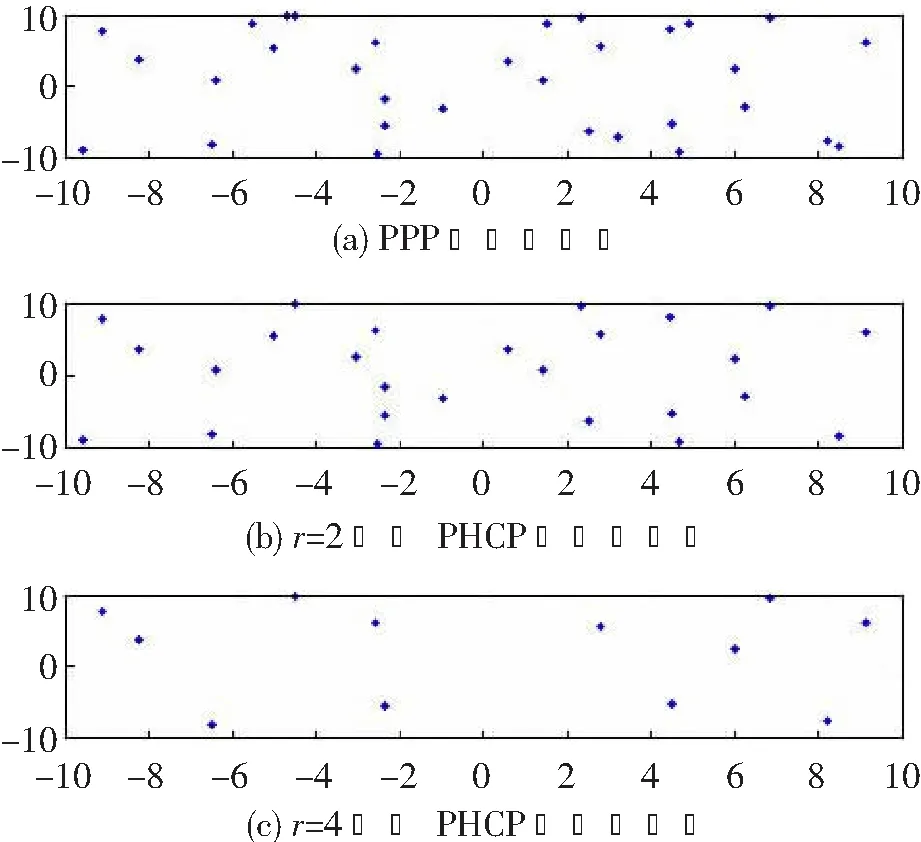
图1 基站分布图

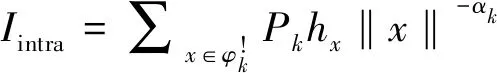
2 基于PHCP的HCN的覆盖性能分析

当用户接入非PPP网络时，将非PPP按照PPP进行处理并且将SIR分布中相应的门限值由θ变为θ/G。同时,来自其他层的干扰假设可以近似为基于PPP网络所引入的干扰。因此，我们将这种方法称为“每层泊松近似方法”。由于PHCP网络基站之间的互斥特性会导致近似干扰在统计上大于实际干扰，由此所产生的近似覆盖率为实际覆盖率的下界。

对于两层HCN的覆盖率：

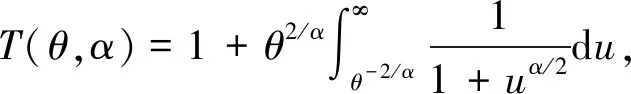
式中：Gk为第k层的近似增益，由文献[7]可知，可通过Gk=MISRPPP/MISRk得到，MISRPPP为PPP的MISR，MISRk为第k层的MISR；λi和λk分别为第i层和第k层的基站密度；δi2/αi，αi为第i层的路损指数。因此，若第k层为PPP时，该层的近似增益为GPPP=1。

对于两层HCN，当用户采用最大接收准则时，其覆盖率可以近似为

更进一步说，

式中：≥为渐近下界，表示近似覆盖率为实际覆盖率的下界。

若HCN中各层网络的路径损耗因子相同，由式(3)可得两层PHCP的近似覆盖率为

式中：λPHCP为宏基站基于PHCP的基站密度；PPHCP为宏基站基于PHCP的发射功率；λPPP为微基站基于PPP的基站密度；PPPP为微基站基于PPP的发射功率；GPHCP为PHCP层的近似增益。

3 仿真分析

本部分通过蒙特卡罗(Monte Carlo)法对PHCP进行仿真，仿真结果是在一个边长为200 m的正方形范围内经过5万次仿真得到。若无特别说明，仿真参数如表1所示。

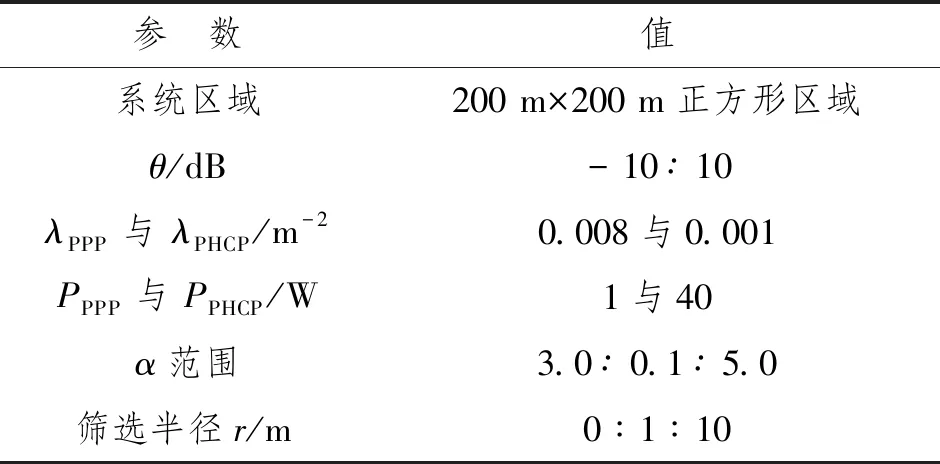
表1 系统仿真参数

3.1 单层PHCP网络的SIR增益

本节通过仿真和数据拟合获取单层PHCP网络的SIR增益。首先分别得到MISR与路径损耗因子α和筛选半径r的关系曲线，并通过数据拟合得到MISR与α和r的关系式，最终求得增益。

图2所示为PHCP的MISR与α及r的关系曲线，利用Matlab软件中的拟合工具箱cftool得到MISR与α和r的关系模型：

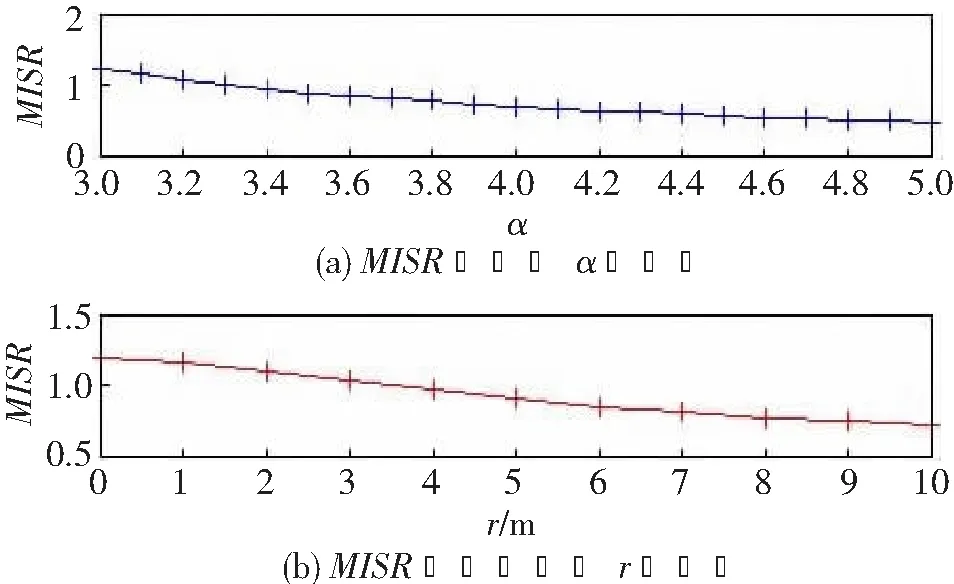
图2 PHCP MISR与路损和筛选距离的关系曲线

其系数如表2所示。

表2 MISR与α和r关系模型系数

由G=MISRPPP/MISR得到PHCP的近似增益GPHCP。最后将GPHCP代入式(6)即可得到两层PHCP HCN的近似覆盖率。

3.2 两层PHCP HCN覆盖率

在本节中，我们对两层PHCP HCN进行仿真分析。首先对两层PPP-PPP和PHCP-PPP网络的仿真覆盖率与理论近似覆盖率进行对比，然后分析PHCP-PPP网络覆盖率与基站筛选半径r的关系。

图3所示为PPP-PPP与PHCP-PPP网络的理论覆盖率与仿真覆盖率。由图可知，两层PHCP网络通过每层泊松SIR近似方法得到的近似覆盖率为实际覆盖率的下界,并且PHCP网络的覆盖性能明显优于PPP网络。

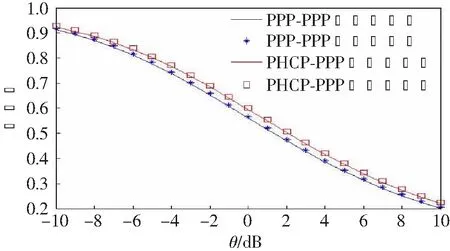
图3 两层PPP-PPP与PHCP-PPP网络的理论覆盖率与仿真覆盖率

图4为两层PHCP网络的理论覆盖率与r的关系图。由图可知，随着r的增大 ，两层基于PHCP的HCN的覆盖率先增大后减小。这是因为随着r的增大，用户接收到来自于宏基站的干扰减少，覆盖性能提升；但是当r过大、宏基站的数量减少过多时，用户能够达到目标SIR的概率反而会减少，从而影响覆盖性能。因此，可以通过适当调节r来提高网络覆盖率。

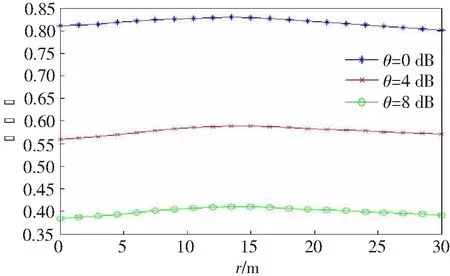
图4 基于PPP-PHCP的HCN的理论覆盖率与r的关系

4 结束语

本文利用每层泊松SIR近似方法实现对两层基于PHCP的HCN覆盖性能的分析。通过仿真与理论的对比，两层基于PHCP的HCN的近似结果是实际异构网络的渐近下边界。同时，仿真结果表明， PHCP网络的覆盖率优于PPP，其更适应于具有互斥性的实际基站部署。