基于二分法改进的Chirp信号参数估计算法
刘国峰,廖 烨,李 康,周文峰
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
近年来无线扩频通信技术飞速发展,以其抗多径衰落、抗干扰、可多址复用和截获概率低等特点在无线通信中被广泛应用。当前扩频技术有直序扩频、跳时扩频、跳频扩频以及线性调频(Linear Frequency Modulation,LFM)[1-2]等。LFM信号又称啁啾(Chirp)信号。Chirp扩频技术广泛应用于雷达、声呐和通信等领域,因此对Chirp信号的检测具有重要的意义。
当前Chirp信号检测方法主要有短时傅里叶变换[3](Short Time Fourier Transform,STFT)、魏格纳-维尔分布[4-5](Wigner-Ville Distribution,WVD)和分数阶傅里叶变换[6](Fractional Fourier Transform,FRFT)等。STFT存在频率分辨率和时间分辨率矛盾等问题;WVD检测多分量Chirp信号时存在交叉项等问题;FRFT进行二维搜索时复杂度高。文献[7]将STFT和Hough变换相结合,用STFT对信号分类,然后对分类后的信号做Hough变换检测出信号;文献[8]提出一种离散FRFT简化算法,降低了复杂度,有助于对Chirp信号进行实时分析;文献[9]提出一种新的LFM信号估计算法,该算法采用等步长搜索调频率,搜索速度慢且没有给出具体的搜索范围,同时没有考虑如何提高相乘后信号频率和中心频率的分辨率。
本文结合STFT粗估计出Chirp信号调频率的范围,在文献[9]的基础上提出一种改进Chirp信号参数估计算法,该算法用二分法代替等步长在粗估计出的范围内搜索调频率,同时采用修正的幅度插值(M-Rife)[10]算法提高该算法估计中心频率的分辨率和修正相乘后信号频谱的幅值,降低了计算复杂度并提升了参数估计精度。
1 Chirp信号简介
Chirp信号的时域表达式为
式中:α(t)为Chirp信号的包络,通常为1;t为时间;j为虚数单位;f0为中心频率;k为调频率(单位是Hz/s),即在一个信号周期内,瞬时频率与时间满足线性关系,斜率为k,k>0为正斜率信号(Up-Chirp),瞬时频率随着时间线性增大,k<0为负斜率信号(Down-Chirp),瞬时频率随着时间线性减小,k=0为频率为f0的单频信号;T为信号周期,也称为信号的扫频时间。B=|k|T为扫频带宽;TB为时间带宽积。
Chirp信号的频谱表达式为
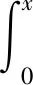
2 STFT
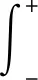
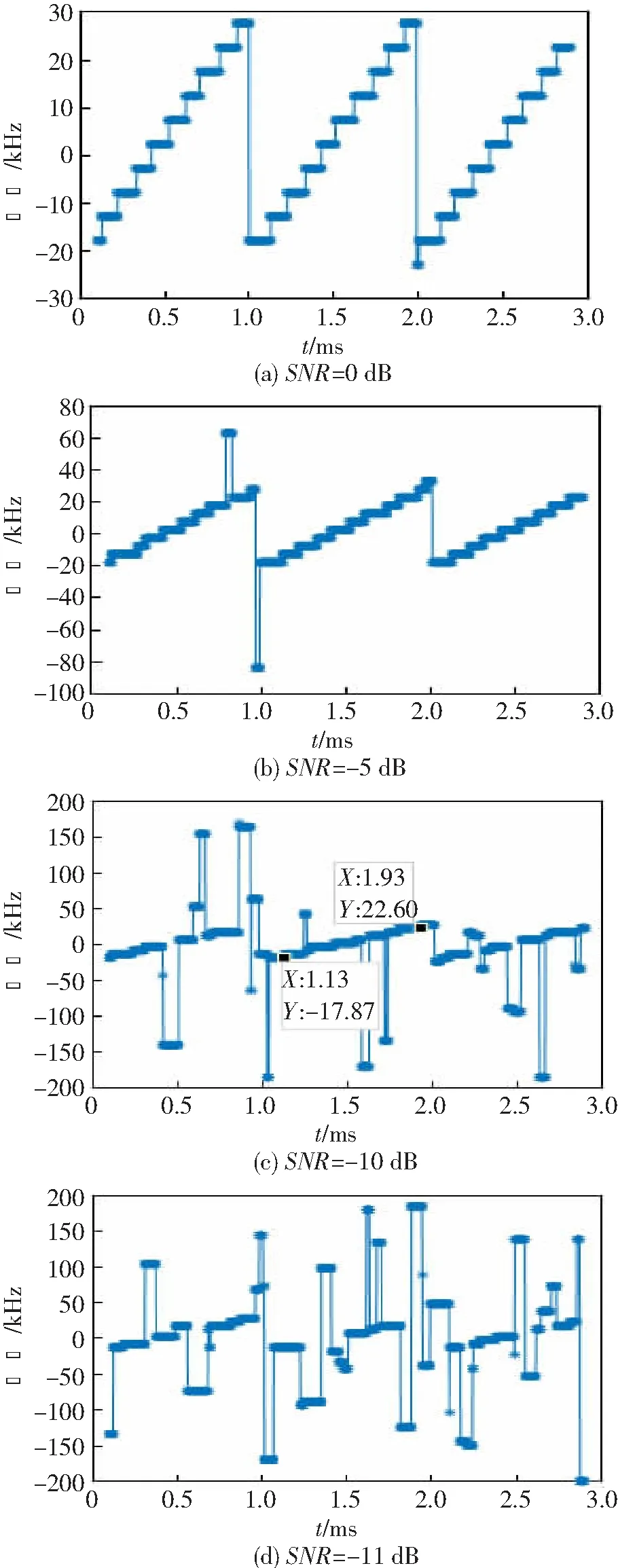
图1 不同SNR下Chirp信号STFT的时频图
在STFT中,窗函数的选取非常重要,常用的窗函数有三角窗、矩形窗、高斯窗、汉明窗和汉宁窗等。在窗函数确定时,STFT中的时间分辨率和频率分辨率随之确定。图1所示为不同信噪比(Signal to Noise Ratio,SNR)下的STFT。Chirp信号的扫频带宽B为50 kHz,中心频率f0为2.5 kHz,信号周期T为1 ms,采样率fs为400 kHz。
由图1(a)~(d)可知,在SNR=0、-5 dB时,可以清楚看出Chirp信号的时频分布,估算出信号的周期时间和调频率的大致范围。在SNR=-10 dB时,虽然受噪声的影响较大,通过舍弃偏远的点和最小二乘法仍然可以估计出信号的周期时间和调频率的大致范围。由图1(c)可知,在SNR=-10 dB时信号的周期时间为1 ms,通过两点间斜率求得调频率大致为5.058 75×107Hz/s,与发送信号的调频率误差在1.175%,并可确定该Chirp信号调频率在4.5×107~5.5×107Hz/s之间,便于后续精确估计调频率和其他参数。由图1(d)可知,在SNR=-11 dB时,已经很难通过最小二乘法估算出Chirp信号调频率的大致范围。虽然STFT存在频率分辨率和时间分辨率的矛盾,但仍可以用来分析Chirp信号并在SNR≥-10 dB时估计出调频率的大致范围。本文主要通过STFT与其他算法相结合,首先估算出调频率的大致范围,由于STFT的抗噪声门限在-10 dB,因此本文主要分析在SNR≥-10 dB时如何更快、更精确地估计出Chirp信号参数。
3 FRFT
FRFT公式为
式中:u为FRFT域;p为阶次;Xp(u)为在阶次p下的FRFT;Kp(t,u)为在阶次p下的FRFT核函数;α=pπ/2为旋转角度;δ(t)为冲击函数;n为整数。当x(t)=exp[j2π(f0t+kt2/2)]时,
当α=arccot(-k)时,其冲击函数为δ(f0-ucscα),能量集中在u=f0/cscα,这称为在对应阶次的FRFT域上Chirp信号的能量聚集,如图2和3所示。因此,可以通过FRFT对Chirp信号进行检测、参数估计以及滤波等。
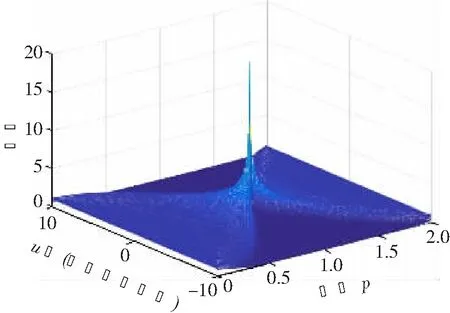
图2 Chirp信号FRFT三维图
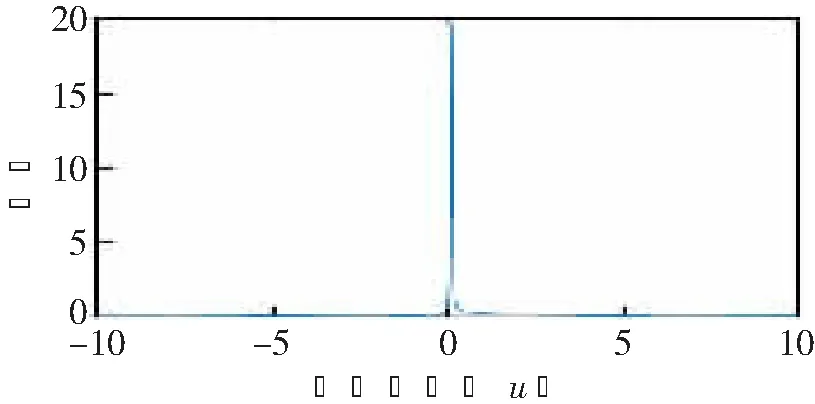
图3 Chirp信号在对应阶次下的FRFT
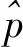

4 改进的新LFM信号估计算法
当时间带宽积TB越大时,Chirp信号频谱越接近矩形,矩形宽度近似于信号带宽B。令x(t)为Chirp信号,频谱为F(f),由帕塞瓦尔能量定理可得x(t)在信号周期上能量为
当TB远远>1时,Chirp信号频谱接近矩形,因此可以用中心频率f0处的频谱幅度A代表整个矩形的幅度,代入式(6)得E≈A2B。由于B=|k|T,代入得E≈A2|k|T。当能量E和信号周期T一定时,Chirp信号调频率k与A2成反比,图4所示为不同调频率下的频谱图。当k无限接近于0时,A无限大。
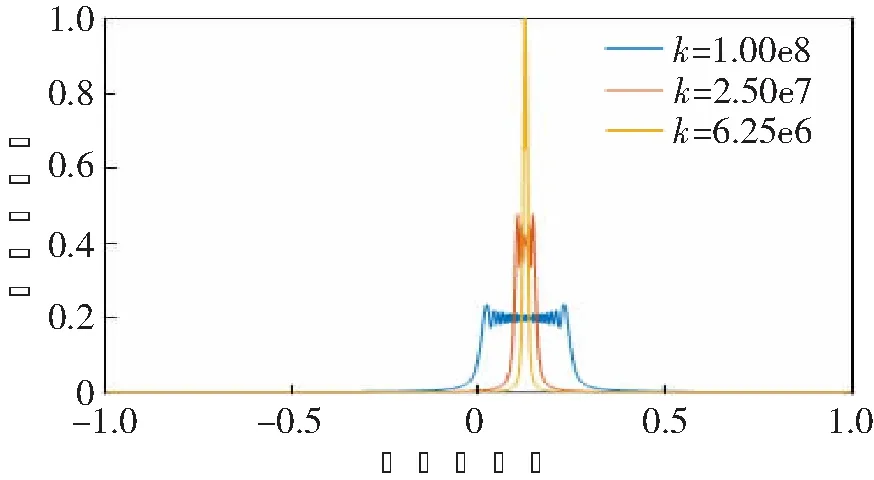
图4 不同调频率下的频谱图
一个Chirp信号乘以exp(-jπkit2)不会改变信号的能量和信号周期,但会使该信号的调频率变为k-ki。若|k-ki|<|k|,则相乘后信号频谱幅度的平方A2会变大,当|k-ki|越来越小时,则相乘后A2会越来越大,即ki越接近真实k,A2越大。当|k-ki|=0时,相乘后信号的调频率为0,此时Chirp信号变为频率为f0的单频信号。由于快速傅里叶变换(Fast Fourier Transform,FFT)的频率分辨率为fs/N,为了更精确地估计中心频率和相乘后的A2,可以采用M-Rife方法。当|k-ki|=0时,可以直接用M-Rife估计出中心频率。对于相乘后信号频谱幅度,首先用M-Rife估计出最大的频率,然后用离散傅里叶变换(Discrete Fourier Transform,DFT)计算出这一点的幅度来表示相乘后的信号频谱幅度。M-Rife计算步骤如下:
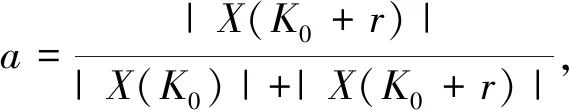
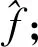
由以上分析可知,关键是找到一个ki使得|k-ki|=0。如果不知道调频率的大致范围盲目地搜索,则效果不好。若已知k的大致范围,如果采用等步长搜索的方法,该方法有缺点。当步长设置过大时,估计调频率的分辨率达不到要求;当步长设置过小时,搜索次数会太多。由于|k-ki|与A2成反比,|k-ki|线性减小时,A2线性增大,也就是说ki与k的差距越小,A2就越大,因此可以采用二分法进行搜索。搜索步骤如下:
步骤1:通过STFT求出Chirp信号x(t)调频率的大致范围[kbeginkend]和信号周期T。
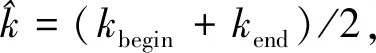
步骤3:分别用exp(-jπkbegint2)和exp(-jπkendt2)与未知信号x(t)相乘,然后通过M-Rife算法求得相乘后信号最大的频谱幅度作为信号频谱幅度,结果分别为Abegin和Aend。执行下一步。
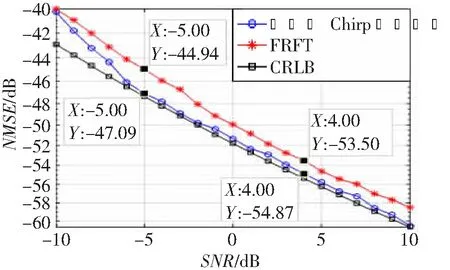
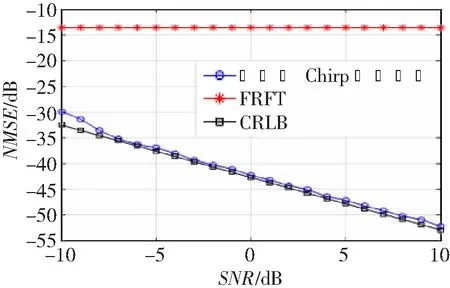
步骤4:比较Abegin和Aend。若Abegin>Aend,说明|k-kbegin|比|k-kend|小,即kbegin比kend更接近k,此时令kend=(kbegin+kend)/2;若Abegin 目前常用的估算Chirp信号参数的方法有FRFT等。对于未知信号,FRFT采用二维搜索,让阶次等步长增加。步长越小,估算的精度越高,但时间复杂度就越大。因此在一个确定的调频率范围内,FRFT的复杂度比改进的Chirp信号估计算法要大。选用第2节中的Chirp信号对比FRFT和改进的Chirp信号估计算法的参数估计性能和抗噪声性能。假设通过STFT估计出调频率的大致范围为4.5×107~5.5×107Hz/s,SNR在-10~10 dB之间,间隔为1 dB。在每个SNR下进行1 000次的Monte Carlo仿真。为了对比算法估计参数的性能,采用归一化均方误差(Normalized Mean Square Error,NMSE)指标来评价。将结果与克拉美罗限(Cramer-Rao Low Bound,CRLB)进行比较,CRLB根据文献[11]计算。仿真结果如图5和6所示。 由图5可知,在SNR≥-10 dB时,改进的Chirp参数估计算法估计的调频率比FRFT效果好,提升大约1~2 dB。由图6可知,在SNR≥-10 dB时,改进的Chirp参数估计算法估计的中心频率明显比FRFT效果好,接近CRLB线。由于存在估计中心频率分辨率过大的问题,FRFT估计中心频率的NMSE没有提升。 图5 不同SNR下调频率估计的误差 图6 不同SNR下中心频率估计的误差 因此改进的Chirp参数估计算法复杂度更低,性能更好,更具有实用性。 本文提出了改进的Chirp信号参数估计,并与STFT相结合。首先用STFT估计出调频率的大致范围和信号周期,然后用二分法通过改进的Chirp信号参数估计算法在这个大致范围内搜索,同时引入M-Rife算法估计中心频率和修正相乘后信号最大频率所对应的幅值,极大地降低了计算复杂度并提升了估计精度。仿真实验表明,在SNR≥-10 dB时,调频率NMSE相对于FRFT提升了1~2 dB,由于采用了M-Rife算法,中心频率NMSE相对于FRFT提升很大。因此针对实际的Chirp信号检测与估计具有很强的实用性和适用性。不足之处在于STFT不能在SNR<-10 dB时对Chirp信号做粗估计,包括调频率和信号周期。下一步将研究如何在更低SNR下对Chirp信号做粗估计。5 仿真结果及性能分析
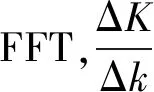
6 结束语

