声线入射角随机模型在深海环境中的应用

马越原，曾安敏，许扬胤，秦显平

声线入射角随机模型在深海环境中的应用

马越原1，曾安敏2，许扬胤1，秦显平2

（1. 信息工程大学，郑州 450001；2. 西安测绘研究所，西安 710054）

为弥补现有适用于深海环境水下定位随机模型研究的不足，提出验证已有的4种顾及声线入射角的随机模型是否适用于深海环境的方法：介绍4种模型的特点；并利用深海实测数据对4种随机模型进行计算分析，来检验随机模型是否具有适用性。结果表明：在深海环境下，采用声线入射角的随机模型进行计算，相对于传统等权模型的定位结果确有改善；但是水下定位结果效果最好的随机模型为指数函数随机模型，而非分段余弦函数随机模型。

水下定位；声线入射角；随机模型；深海环境；实测数据

0 引言

海洋是全人类可持续发展的重要空间，是资源勘探和开发的主要区域，而高精度、高可靠的海底控制网正是进行海洋探测、开发的重要参考基准[1-3]。海底控制网是通过在海底布设声学基准站组成类似全球卫星导航系统（global navigation satellite system, GNSS）星座、用于水下定位的系统。要想得到高精度的水下定位结果，除了要有正确的定位函数模型，还需要选择正确的随机模型。在很多文献关于水下定位的计算过程中，所采用的随机模型基本上都是等权模型，即认为每个历元观测量的方差是相等的。该模型虽然应用简单，但是由于水下环境极其复杂，简单地应用等权随机模型必然与实际情况不符，从而影响水下定位精度。

目前国内外学者针对水下定位随机模型的相关研究并不多，已有的研究基本上都是基于浅海环境的模拟仿真结果。众所周知，浅海环境与深海环境存在相当大的区别，除了在物理环境上的差异外，浅海和深海在声学上的差异也是非常明显的[4]。而水下定位主要是依靠声学测距，因此适用于浅海环境的随机模型不一定完全适用于深海环境。

本文的主要目的，就是考察已有的声线入射角随机模型是否适用于深海环境，并用实测数据对研究结果进行验证。

1 水下定位函数模型

水下定位目前通常采用测量船圆走航的方式，其定位原理如图1所示。

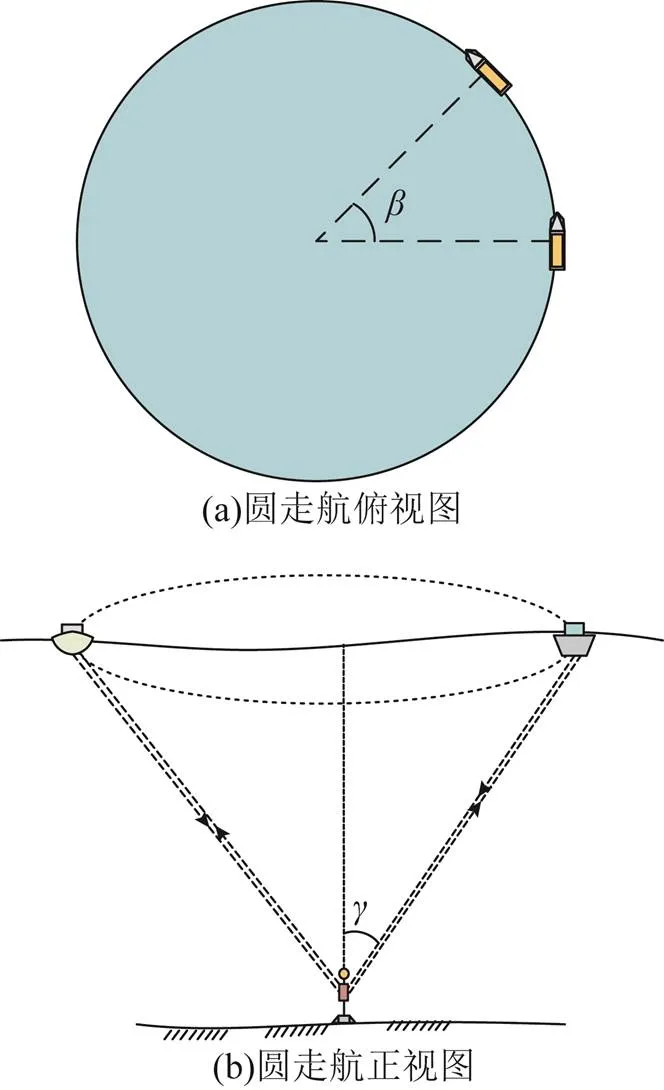
图1 圆走航基本原理

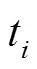
将式（1）通过泰勒级数展开的方法进行线性化可得

将式（2）表示为矩阵形式，即

因此，在不考虑系统误差的情况下，误差方程可以写成：

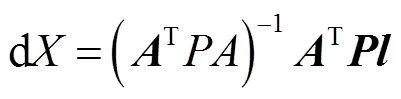
式中：为观测值改正数矩阵；为权矩阵

2 基于声线入射角的函数模型

有文献指出，目前水下定位常用的随机模型普遍采用等权模型，认为测量船每个历元对各个应答器的观测量为独立、等精度观测量，其先验方差相等[6-7]。众所周知，海洋环境复杂，水下定位依靠声学测距，该距离则通过声线波束在海水中传播时间的测量，以及声速剖面的测量获得，而海水中的声速又受压强、温度、盐度的综合影响[8]；所以在实际情况中，影响水下定位精度的因素非常多，利用简单的等权模型进行计算得到的结果，必然精度较差。因此，研究更贴近实际情况的水下定位随机模型是必要的。

除了粮食运输，对于钢材与矿石运输的影响不大。2017年中国直接出口美国钢材占出口总量1.57%。由于钢铁“去产能”，加上美国长期对中国钢材产品进行贸易调查，中国出口至美国的钢材持续呈现下降的态势。加税难以改变中国钢铁生产趋势，对上游铁矿石进口影响同样不大。

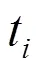
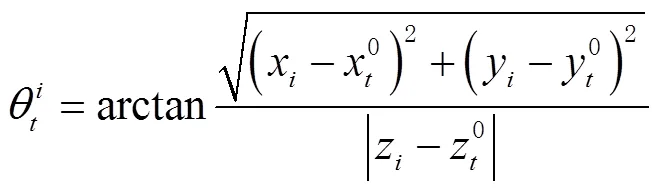
前面已提到入射角越大，声速误差的影响越大，因此认为声线入射角越大，观测量先验方差越大。由此，文献[6-7]中提出了具有代表性的一般比例函数、三角函数和指数函数这3类相关函数，并且构造出4种关于声线入射角的随机模型，表达式为：

1）一般正比例函数

2）入射角余弦函数

3）入射角指数函数

4）入射角分段余弦函数

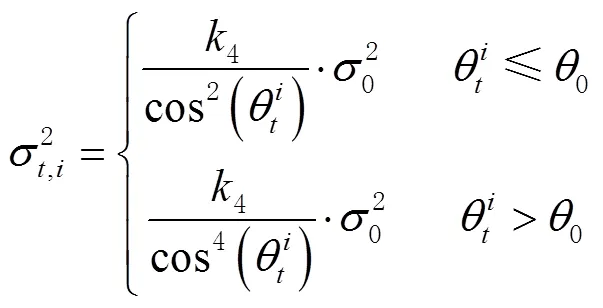
为了确保计算结果更具有说服力，在采用各随机模型计算时，随机模型中的常数项与文献[6]中的取值一致。

水下应答器对应的各历元观测量的方差矩阵为

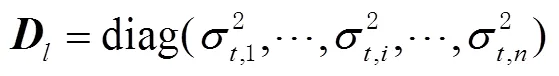
观测量的权矩阵为

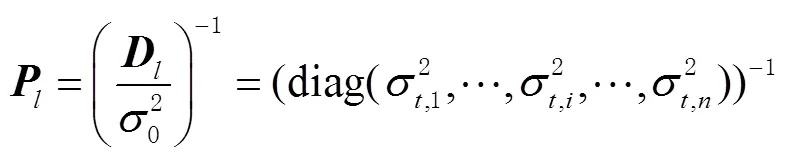
可知应答器位置改正数及观测值改正数为

3 实验与结果分析

文献[6]中提到在南海水深接近100 m的浅海海域进行了实验，实验显示所提出的随机模型确实在不同程度上改善了等权模型的定位结果，尤其是分段余弦的入射角随机模型定位结果最好。

我国南海海域平均水深在3000 m左右，仅仅利用在100 m左右水深海域的实测数据进行随机模型的计算，其声速误差和声线弯曲的影响并不足够显著，因此为了验证其结果是否具有普遍性，即是否适用于深海环境，在所提出的随机模型的基础上，本文开展了验证实验。此次验证实验数据源于2019年7月，在南海水深超过3000 m的某海域所进行的观测实验。

观测海域的实测声速剖面如图2所示。

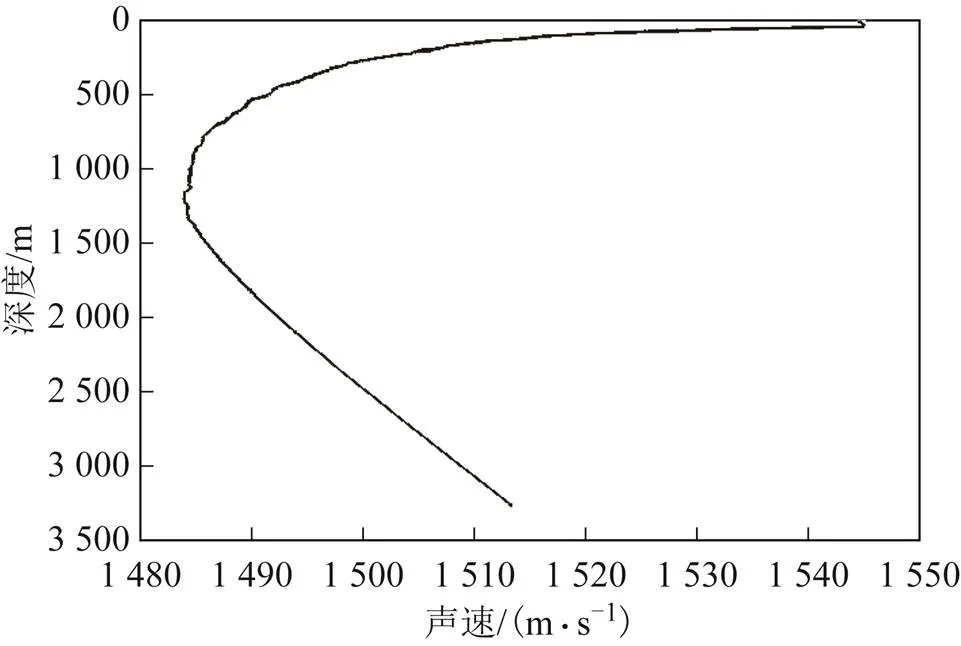
图2 实测海域声速剖面

实验过程中采用圆走航的方式，对布设的海底基准进行实验性观测。根据式（6）计算得出在不同历元下，声线入射角的变化，如图3所示。

图3 不同观测历元下的声线入射角

鉴于实测数据中难免有很多粗差，因此需考虑观测历元数量及数据质量。通过抗差处理之后，选取684个历元的数据进行计算，平均声线入射角为68.07°，最大声线入射角为89.9°，最小声线入射角为42.11°。由于此次实验属于海底基准点精度观测实验，没有准确的真值来计算外符合精度，故本文仅通过最小二乘计算得到观测值改正数，并计算其均方根(root mean square, RMS）值作为内符合精度来进行比较。

统计各随机模型下定位解算RMS值，如表1所示。

表1 不同随机模型下定位解算RMS值 单位：m

由表1可知，文献[6]提出的4种随机模型，的确从不同程度上改善了等权随机模型的定位结果，但是效果最好的并不是分段余弦函数的随机模型，而是指数函数的随机模型。可见复杂的海洋环境中，存在着众多的不确定因素影响着声学定位的精度；因此在构造随机模型时，不能只简单地考虑单一的函数形式，某种函数的随机模型适用于某一片海域，却不适应于另一片海域。

4 结束语

本文主要针对文献[6]提出的4种声线入射角随机模型，在深海海域中的应用进行了验证实验，利用深海实测数据分别计算了等权随机模型、一般正比函数随机模型、余弦函数随机模型、指数函数随机模型以及分段余弦函数随机模型下的水下定位结果改正数的RMS值，分别为0.4763、0.4568、0.5044、0.4544、0.4688 m，相对于等权模型，其它随机模型不同程度地改善了定位结果，但是效果最好的并不是文献[6]所得出的分段余弦函数随机模型，而是指数函数随机模型。

综上所述，海洋环境复杂，同时浅海环境与深海环境也存在着巨大的差异，影响声学定位精度的因素众多，因此构造水下声学定位随机模型时，需要用不同海域的实测数据进行大量的计算分析。关于模型的进一步优化完善，有待后续深入研究。

[1] 杨元喜, 徐天河, 薛树强. 我国海洋大地测量基准与海洋导航技术研究进展与展望[J]. 测绘学报, 2017, 46(1): 1-8.

[2] 李林阳, 吕志平, 崔阳. 海底大地测量控制网研究进展综述[J]. 测绘通报, 2018 (1): 8-13.

[3] 赵建虎,梁文彪.海底控制网测量和解算中的几个关键问题[J]. 测绘学报, 2019, 48(9): 1197-1202.

[4] KATSNELSON B, PENTNIKOV V, LYNCH J.浅海声学原理[M]. 程广利, 张亚蕾, 译. 北京: 电子工业出版社, 2018: 2-3.

[5] XU Peiliang, ANDO M, TADOKORO K.Precise, three-dimensional seafloof geodetic deformation measurements using difference techniques[J]. Earth, Planets and Space, 2005, 57(9): 795-808.

[6] 赵爽, 王振杰, 刘慧敏. 顾及声线入射角的水下定位随机模型[J]. 测绘学报, 2019, 47(9): 1280-1289.

[7] ZHAO Shuang, WANG Zhenjie, HE Kaifei, et al.Investigation on underwater positioning stochastic model based on acoustic ray incidence angle[J]. Applied Ocean Research, 2018, 77: 69-77.

[8] 汪德昭, 尚而昌.水声学[M]. 2版.北京: 科学出版社, 2013.

[9] 吴永亭. LBL精密定位理论方法研究及软件系统研制[D].武汉: 武汉大学, 2013.

[10] 杨豪强, 贺秋瑞, 漆世凯, 等. 水下目标定位中的声线折射修正方法[J]. 河南师范大学学报(自然科学版), 2012, 40(1): 36-39.

Application of incidence angle stochastic model of acoustic lines under deep sea environment

MA Yueyuan1, ZENG Anmin2, XU Yangyin1, QIN Xianping2

（1. Information Engineering University, Zhengzhou 450001, China; 2. Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China）

In order to make up for the insufficiency of studying on the stochastic model of underwater positioning under deep sea environment, the paper suggested to verify the applicability of existed 4 stochastic models which take into account the incident angles of acoustic lines under deep sea environment: the characteristics of the 4 models were introduced, and the measured data of the deep sea were used to calculate and analyze the models to test their feasibility. Results showed that the positioning accuracy of the stochastic model based on the incidence angle of acoustic lines would be higher than that of the traditional equal weight model; while the best stochastic model for underwater positioning would be the exponential function stochastic model, rather than the segmented cosine stochastic model.

underwater positioning; acoustic line incidence angle; stochastic model; deep sea environment; measured data

P228

A

2095-4999(2020)03-00065-04

马越原，曾安敏，许扬胤，等. 声线入射角随机模型在深海环境中的应用[J]. 导航定位学报, 2020, 8(3): 65-68.（MA Yueyuan, ZENG Anmin, XU Yangyin,et al. Application of incidence angle stochastic model of acoustic lines under deep sea environment[J]. Journal of Navigation and Positioning, 2020, 8(3): 65-68.）

10.16547/j.cnki.10-1096.20200310.

2020-03-09

国家重点研发计划项目（2016YFB0501700, 2016YFB0501701）；国家自然科学基金项目（41931076, 41874016, 41604013）。

马越原（1991—），男，湖南岳阳人，博士研究生，研究方向为海洋大地测量。