高中数学解题经验对数学学习的影响
张想成
高中阶段学生开始逐渐接触更高深、难度更大的数学知识,高中数学的学习,不仅要引导学生深入把握基础的概念知识,还需要学生对数学核心思想有明确的认识.解题的实质就是解决问题的过程,具备鲜明的实践性与探索性,学生要能够通过对数学问题的解答,来促进自身对数学知识的理解与掌握,锻炼自己基本数学技能,推动自身逻辑思维的建立.数学解题经验就是将相关的数学知识、方法以及条件进行总结得到的成果.高中数学解题经验对高中数学学习具有十分重要的意义.本文结合相应的例题与解析,探讨高中数学解题经验对数学学习的影响.
1 解题经验对知识融合与综合应用能力有积极影响
不同学生的解题能力也有所不同,解题经验的积累可以帮助学生更好地实现知识融合,培养学生综合应用能力.

A. [0,1] B. [0,2] C. [0,e] D. [1,e]

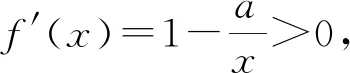
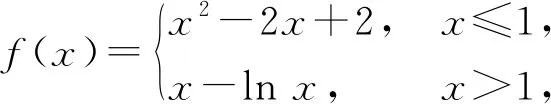
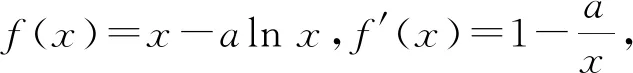
综上所述,a的取值范围为0≤a≤e,故选C.
2 解题经验对提高学生学科素养有积极影响
高中数学教学中长期进行解题教学,可以帮助学生提升数学学科素养.例如,在函数学习中,学生需要掌握函数的基本概念、性质及函数图象等内容.解题经验的积累对提高学生核心素养,提高学生理解能力与解题能力效果较为明显.

①f(x)是偶函数;
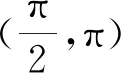
③f(x)在[-π,π]有4个零点;
④f(x)的最大值为2.
其中正确的结论编号为( ).
A. ①②④ B. ②④ C. ①④ D. ①③

由f(-x)=sin|-x|+|sin(-x)|=sin|x|+sin|x|=f(x),易知f(x)是偶函数,因此①正确.
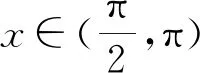
当x∈[0,π],f(x)=sinx+sinx=2sinx,函数存在2个零点,f(0)=f(π)=0,且x∈[-π,0]时,f(0)=f(-π)=0,故函数有且仅有3个零点,因此③ 错误.
因为函数为偶函数,所以在判断最大值时,仅需要讨论x>0的情况.当x∈[2kπ,π+2kπ](k∈N)时,f(x)=sinx+sinx=2sinx,最大值为2;当x∈[π+2kπ,2π+2kπ](k∈N)时,f(x)=sinx-sinx=0,故函数最大值为2.因此④正确,故选C.
良好的数学思维是学生在高中阶段数学学习必须具备的核心素养,对学生的数学学习乃至日后的生活与工作都会产生影响.教师在高中数学的日常教学中,应积极地引导学生养成良好的解题习惯,建立合理有效的数学解题思路,提高解题效率.在解题方法的寻找过程中,要注意数学知识与数学技巧的有机融合,将数学思维贯穿于整个过程中,提高学习效率.

