探究方差大小比较问题

王玉泉

概率与统计问题是历年高考和模拟考试中的重要题型之一,其中“比较方差大小”是一个高频考点,能综合考查学生的数据分析与处理能力．在教学过程中，教师应该引导学生利用方差的实际意义,借助数学直观,归纳出一些规律与方法,以便快速准确地解决问题,从而有助于提升学生对数据的判断与决策能力,培养学生的数学核心素养．

1 方差定义的三种形式及应用

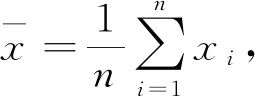
证明

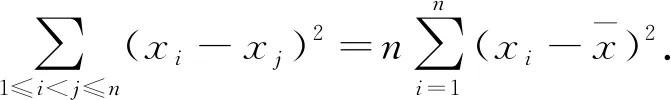
因此，方差有三种形式的定义式，即

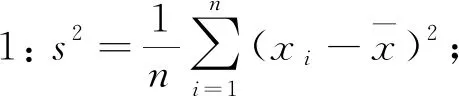
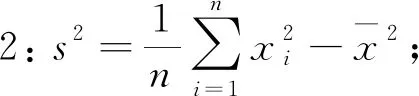
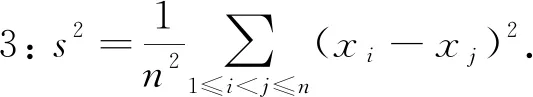
证明(1)略.

(2)利用方差定义式3可得

方差定义式1是教材中给出的形式,定义式2是其简化形式．方差是各变量值与其均值离差平方的平均数,是测算数据离散程度的重要方法,它反映了一组数据与其平均值的偏离程度．因此，方差越大,数据的波动越大;方差越小,数据的波动就越小．在教学实践中,教师常常要求学生会比较方差大小,但不要求掌握证明方法．一些简单问题容易解决,但是一些复杂问题仅仅依靠数学直观难以解决,如果利用定义计算又比较烦琐,所以探寻一些快速解题的方法很有必要．定义式3是笔者个人总结的,它给出了方差的另一个意义:数据两两之间差值平方的平均(注意分母是n2),当样本容量n比较小时(如n=3或n=4)可以不借助均值做一些简单的估算,从而快捷高效地解决问题．

2 比较方差大小的有关结论

利用定理1和定理2可以推导出一些结论,对于解题很有帮助，常见结论如下.

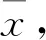
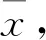
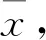
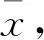
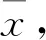
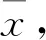
3 比较方差大小问题的实际应用

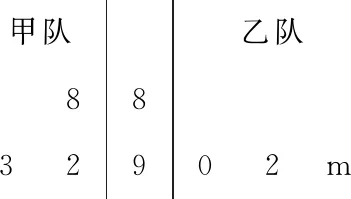
表1

乙队记录中有一个数字模糊(表1中阴影部分),无法确认,假设这个数字具有随机性,并用m表示.

(1)在4次比赛中,求乙队平均得分超过甲队平均得分的概率;

(2)当m=5时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2次比赛得分之差的绝对值为X,求随机变量X的分布列;

(3)如果乙队得分数据的方差不小于甲队得分数据的方差,写出m的取值集合(结论不要求证明).

(3)甲队数据同时减去88得0,3,4,8,方差不变,乙队数据同时减去89得0,3,4,m+1，方差不变.如果乙队得分数据的方差不小于甲队得分数据的方差,则可用以下两种方法求解.

方法2 利用方差的实际意义，m+1≥8,故m取值的集合为{7,8,9}．

甲队乙队8832902m

图1

(1)在3次比赛中,求乙队平均得分超过甲队平均得分的概率;

(2)当m=5时,分别从甲、乙两队的3次比赛中各随机选取1次,记这2次比赛得分之差的绝对值为X,求随机变量X的分布列和数学期望；

(3)若在3次比赛中,甲队得分的方差比乙队得分的方差小,写出m的可能取值(结论不要求证明).

(3)若在3次比赛中,甲队得分的方差比乙队得分的方差小,利用方差定义式3，只需(88-92)2+(88-93)2+(92-93)2<[(90-92)2+(90-90-m)2+(92-90-m)2],即m2-2m-17>0,故m的可能取值为6,7,8,9.

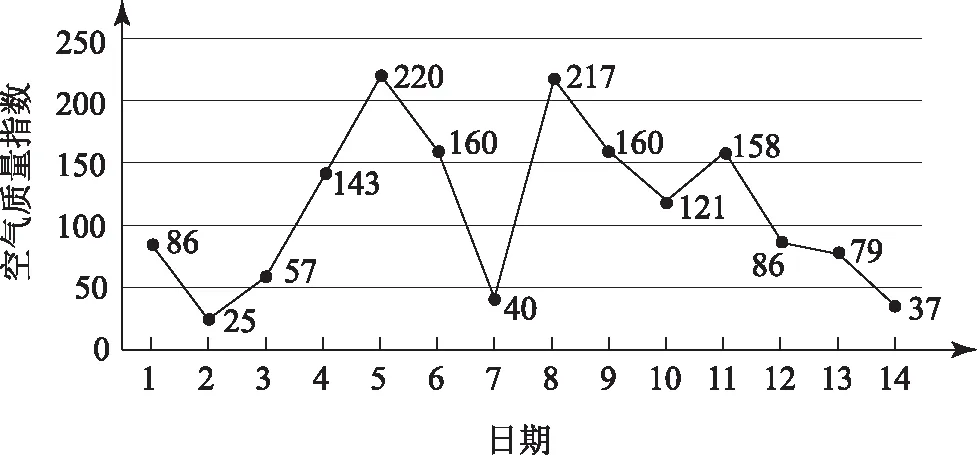
图2

(1)求此人到达当日空气重度污染的概率;

(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;

(3)由图判断从哪天开始连续3天的空气质量指数方差最大(结论不要求证明).

(3)连续3天的空气质量指数方差最大只能在空气质量指数为57,143,220或40,160,220之间产生.

方法1 利用方差定义式3,(220-160)2+(220-40)2+(160-40)2-[(220-143)2+(220-57)2+(143-57)2]=602+1802+1202-(772+1632+862)=(602-772)+(1802-1632)+(1202-862)>0.故40,160,220的方差最大,即从3月5日开始连续3天的空气质量指数方差最大．

当前已进入大数据时代,基于数据的合理判断与优化决策也成为一种必备能力．在教学实践中,概率统计部分常以比较方差大小问题为切入点,培养学生的数据收集、分析、处理能力,从而有助于提升学生数学核心素养．

链接练习

已知有下列数据.

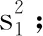
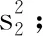
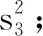
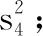
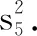
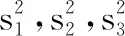
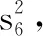
链接练习参考答案