函数图象变换的规律及应用
陈上太
从高考的命题趋势来看,函数图象变换是高考的热门考点,在函数、三角函数中都有涉及,能综合考查考生的数形结合能力以及逻辑推理能力.函数图象的变换主要是指函数图象的平移变换、伸缩变换、对称变换等.本文主要总结函数图象变换的规律,并指导考生运用这些规律去解答相关的高考题.
1 函数图象变换的规律
1.1 平移变换
1)把函数y=f(x)的图象向左平移a(a>0)个单位,可得函数y=f(x+a) 的图象;把函数y=f(x)的图象向右平移a(a>0)个单位,可得函数y=f(x-a)的图象;
2)把函数y=f(x)的图象向上平移b(b>0)个单位,可得函数y=f(x)+b的图象;把函数y=f(x)的图象向下平移b(b>0)个单位,可得函数y+b=f(x)(即y=f(x)-b)的图象.
1.2 伸缩变换
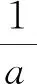
2)函数y=Af(x)(A>0且A≠1)的图象是把函数y=f(x)的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0 1)y=f(x)与y=f(-x)的图象关于y轴对称; 2)y=f(x)与y=-f(x)的图象关于x轴对称; 3)y=f(x)与y=-f(-x)的图象关于原点对称; 5)y=f(x)关于点(a,b)对称的函数是2b-y=f(2a-x) (即y=2b-f(2a-x)). 将函数y=sinx依次进行如下变换: A. 3x-2y+2=0 B. 2x+3y+7=0 C. 3x-2y-12=0 D. 2x+3y+8=0 (1)写出曲线C1的方程; y=(x-t)3-(x-t)+s. (2)在曲线C上任取一点B1(x1,y1),设B2(x2,y2)是B1关于点A的对称点,则有 所以x1=t-x2,y1=s-y2. 代入曲线C的方程,得x2和y2满足方程: s-y2=(t-x2)3-(t-x2), 即 y2=(x2-t)3-(x2-t)+s. 故点B2(x2,y2)在曲线C1上. 反过来,同样可以证明在曲线C1上的点关于点A的对称点在曲线C上.因此,曲线C与C1关于点A对称.1.3 对称变换

2 函数图象变换规律的应用
2.1平移变换

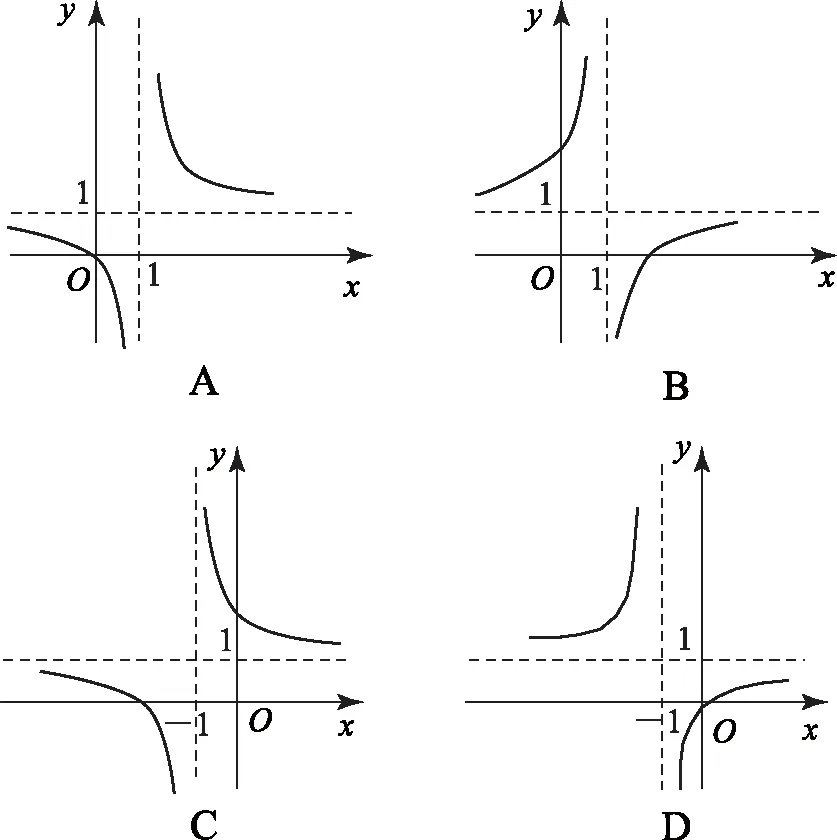

2.2 平移和伸缩变换


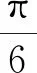
2.3 对称变换


2.4 平移与对称变换

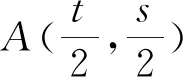

——从广州一模的一道选择题谈起

