激光器线宽对谐振式光纤陀螺标度因数的影响

司 琪，冯 喆，于昌龙，孙桂林，于怀勇，雷 明

（北京自动化控制设备研究所，北京100074）

谐振式光纤陀螺是基于光学Sagnac效应来检测载体相对于惯性空间的旋转角速度的传感器件[1-3]，采用光纤环形谐振腔作为核心敏感部件，通过测量谐振腔顺时针和逆时针两路光的谐振频率的差值来得到转动角速度。在谐振式光纤陀螺系统中，具有一定线宽的激光器的相干长度会影响谐振腔输出的干涉光之间的相干度，造成谐振峰的展宽，影响谐振腔的清晰度。因此，随着激光器线宽的加宽，会使得谐振腔的谐振特性变差。为得到较好的谐振特性，以及为便于小型化应用，常使用连续可调谐的窄线宽半导体激光器作为光源。但是由于半导体激光器加工工艺的影响，其输出并不是理想的单频光，并且受外围驱动电路性能和温度漂移的影响，其线宽会发生不同程度的展宽。激光线宽的展宽制约着谐振式光纤陀螺的发展，因此定量分析半导体激光器线宽对陀螺性能的影响，不仅对激光器驱动的设计具有理论指导作用，更对谐振式光纤陀螺的发展具有重要意义。

在激光器对谐振式光纤陀螺影响的研究中，2003年浙江大学马慧莲课题组在激光器线宽对谐振式光纤陀螺谐振腔清晰度测试以及陀螺极限灵敏度的影响方面作出了一定的理论分析[4]，而近几年针对激光器线宽的研究较少。2015年北京航空航天大学的冯丽爽课题组在激光器强度噪声对谐振式光纤陀螺的影响方面取得了较好的进展，并有效抑制了由激光器电流调谐导致的激光强度噪声[5]。在以往的研究中，尚没有在激光器线宽对谐振式光纤陀螺标度因数的影响上进行深入分析。标度因数的大小直接反应了陀螺的检测精度，因此，对陀螺中激光器线宽对陀螺标度因数的影响进行分析，控制激光器线宽以获得较大的标度因数是非常有必要的。

当谐振式光纤陀螺系统中增益保持恒定时，其标度因数与陀螺解调曲线的斜率（斜率绝对值）成正比。因此本文针对谐振式光纤陀螺的动态性能，理论分析光纤谐振腔解调曲线的斜率受激光器线宽的影响，并利用半导体激光器和16m长、清晰度为43的光纤谐振腔搭建实验系统进行实验验证，从而确定激光器线宽的展宽会非线性地减小标度因数的结论，进一步以半高全宽为300 kHz的谐振式光纤陀螺仪为例，得出陀螺标度因数在1% 范围内变化时其激光器线宽应保持在 3 kHz以内的要求。

1 谐振式光纤陀螺谐振腔解调输出理论模型

陀螺的开环结构框图如图1所示。半导体激光器（Laser）发出的光经过隔离器（ISO），在Y波导上分成两束并进行余弦波相位调制后进入透射式光纤谐振腔，在谐振腔内发生多光束干涉后，经耦合器输出并进行解调，解调结果由光电探测器PD1和PD2转换为电信号后分别用于激光器锁频和陀螺输出。由于探测器PD1与PD2的输出线型相同，同时为避免两路光同时输入谐振腔造成背反噪声的干扰，本文选取图中虚线部分作为研究对象，并在后续试验中将Y波导的一条支路Y-2以及探测器PD2断开。

图1 谐振式光纤陀螺开环结构框图Fig.1 The block diagram of resonant fiber optic gyroscope

在谐振式光纤陀螺系统的理论研究中，通常假设作为光源的半导体激光是理想的（单频光），其电场E(t)为：

其中，E0为激光振幅，ω=2πf（f为激光器中心频率）。半导体激光器发出的光在经过Y波导上的余弦调制后变为Ein(t)：

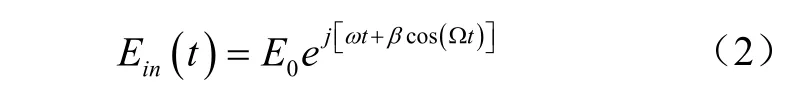
其中，βcos(Ωt)为余弦调制信号，β为调制深度，Ω为调制频率。调制后的光经过光纤谐振腔的传输，并最终由透射端输出。透射端输出电场的贝塞尔展开为EPD1(t)：

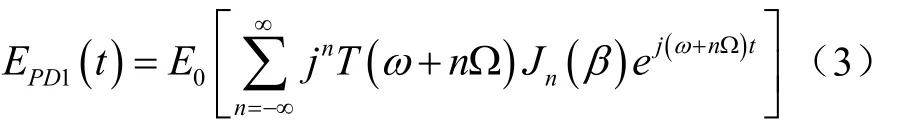
其中T(ω)为光纤谐振腔透射端的电场传递函数[6]。根据式（3），进一步将透射端电场的传递函数转化为光强的传递函数为：

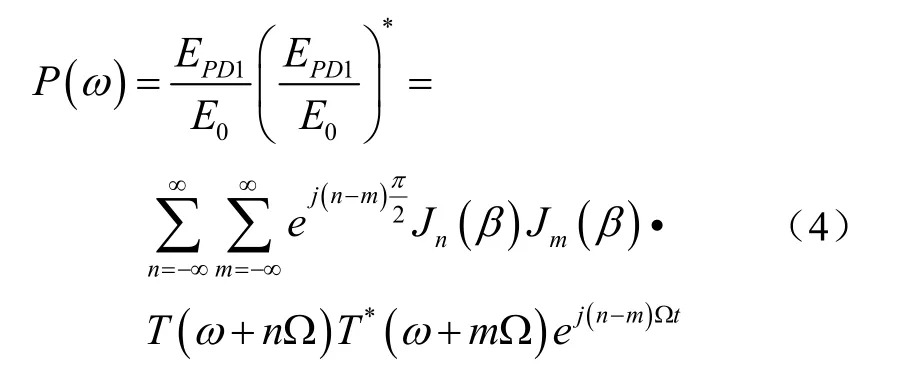
以上通过分析激光器理想状态时谐振式光纤陀螺光路的传输模型，从而得到谐振腔透射端的传递函数。通过固定的谐振腔参数对式（4）进行仿真，结果如图2所示，根据仿真结果可以看出该传递函数的半高宽为300 kHz。

图2 谐振腔透射端传递函数模型Fig.2 Transfer function model of transmission end of resonator

由于激光器发出的光在Y波导上经过了余弦相位调制，在谐振腔透射端输出后需对其进行余弦解调处理，并经过数字低通滤波器滤除高次谐波后，可得到谐振腔透射端解调输出的传递函数I(ω)为：

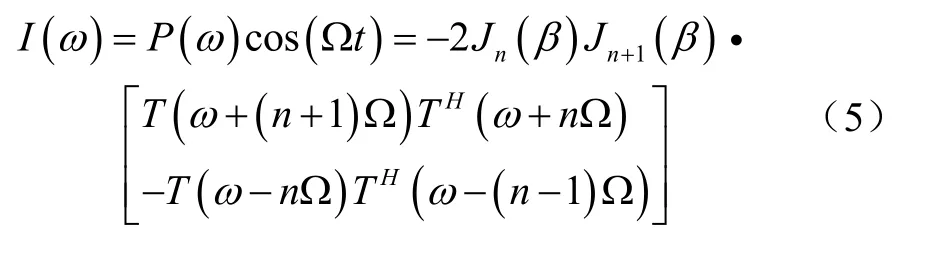
然而在实际应用中，激光器发出的光不是理想的单频光，且具有不同程度的线宽展宽。接下来，本文对激光器处于非理想状态时谐振式光纤陀螺谐振腔透射端的解调输出信号进行研究。

普通激光器的光谱线型和线宽主要是由频率噪声所决定的，包括白噪声和1/f噪声[6]。对半导体激光器而言，其光谱线型以及线宽的展宽主要是受到白噪声的影响。在白噪声的影响下，半导体激光器的光谱线型是洛伦兹型，因此其光谱的函数表达式可以写为[7,8]：

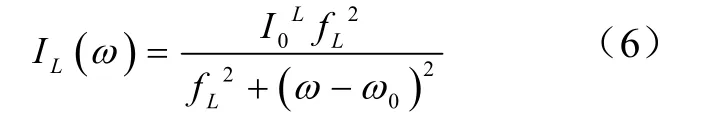
其中，fL是半导体激光器的线宽，I0L是半导体激光器中心频率处的光强，ω0是半导体激光器的中心频率。对式（6）进行积分，可得到半导体激光器输出光强ILaser的表达式为[9]：

当驱动电流不变时，半导体激光器的输出光强不变，即在一定驱动电流下，ILaser为定值。为方便计算，将式（6）改写为：

谐振式光纤陀螺中，半导体激光器发出的光经过Y波导和谐振腔的传输过程，在数学上可理解为激光器光谱函数与陀螺光路传递函数的卷积过程[10,11]。令δω=ω-ω0，根据式（5）和式（8）可以求出谐振腔透射端的解调输出信号IOUT(ω)的表达式为：

2 谐振式光纤陀螺谐振腔解调输出模型仿真

将激光器输出光强ILaser归一化为1，分别取激光器线宽为1.5 kHz、3 kHz、15 kHz、50 kHz、150 kHz和300 kHz，对式（9）进行仿真，得到谐振腔透射端输出的解调曲线IOUT(Δf)，如图3所示。其中Δf为激光器频率与谐振腔谐振频率的差值，Δf=(ω-ωresonant)/2π，且ωresonant为陀螺谐振腔谐振频率的角频率。在实际应用中，每次启动时陀螺系统的初始相位是不确定的，若进行多次重复试验，则会引入相位抖动带来的误差。为消除这种误差的影响，本文在后续试验中采取直接测试|IOUT(Δf)|（实虚部平方和的算术平方根）的方式对谐振腔透射端输出的解调曲线斜率进行计算。根据图3可以得到|IOUT(Δf)|的理论图形，如图4所示。

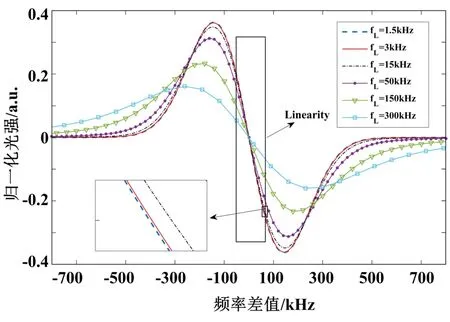
图3 光纤谐振腔解调输出曲线Fig.3 The demodulation output curve of fiber cavity

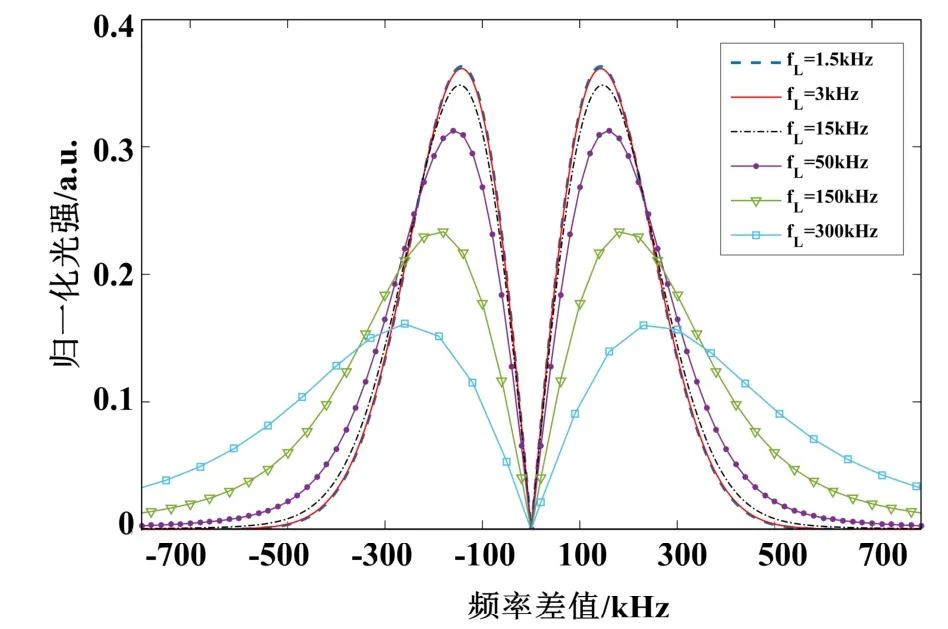
图4 光纤谐振腔解调曲线的模Fig.4 The absolute value of the demodulation output curve of fiber cavity

从图3、图4中可以看出，随着激光器线宽的增大，谐振腔透射端输出的解调曲线的斜率在逐渐减小，导致陀螺的标度因数也在减小。对不同激光器线宽下的陀螺解调曲线斜率进行进一步计算，分析得到解调曲线斜率变化1%，也即陀螺标度因数变化1%的激光器线宽范围。

在上述理论计算中，已将激光器光强归一化为1[12]，并且没有引入环路增益，解调曲线斜率的理论值与实际测量值将会有很大不同。因此本文通过计算解调曲线斜率变化的百分比来比较理论与实验中不同线宽之间斜率的差异，从而验证理论分析的正确性。首先根据式（5）可以求出在理想状态时解调曲线斜率约为4.03×10-7。同时，对图3进行计算并拟合得到解调曲线斜率与激光器线宽的关系曲线，如图5所示。

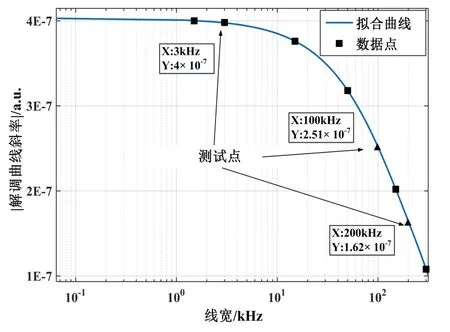
图5 解调曲线斜率与激光器线宽的关系曲线Fig.5 Relation curve between slop of demodulation curve and line width of laser

根据图5的曲线可以看出，当半导体激光器的线宽为3 kHz时，归一化的解调曲线斜率约为4×10-7，与理想状态时相差0.74%。而当半导体激光器线宽大于3 kHz时，解调曲线的斜率不断减小。由于陀螺的标度因数与解调曲线斜率成正比关系，所以陀螺标度因数与激光器线宽的关系同样符合图5曲线。因此对于半高宽为300 kHz的谐振腔，为保证标度因数偏离理想状态的程度不超过1%，应将激光器线宽控制在3 kHz以内。

3 试验验证

根据图1，采用腔长为16 m，折射率为1.45，清晰度为43，半高宽为300 kHz的光纤谐振腔搭建实验系统。通过改变驱动电路的带宽来控制半导体激光器的线宽，测试在不同激光器线宽下，光纤谐振腔的解调输出变化。为确定激光器的线宽，首先采用N1601C单频激光器噪声测试仪测试了激光器在不同驱动状态下的频率噪声，测试曲线如图6所示。激光器线宽fL的表达式[6,13]为：

其中C为半导体激光器白噪声的功率谱密度，单位为Hz2/Hz。根据图6的测试结果可以计算出激光器的三种线宽分别约为3 kHz、100 kHz、200 kHz。

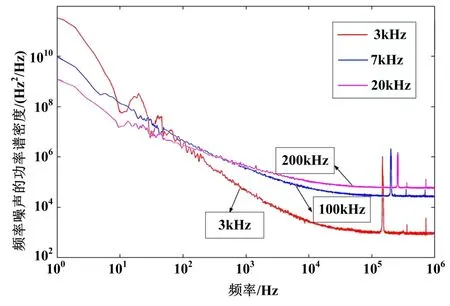
图6 半导体激光器频率噪声测试图Fig.6 The test image of semiconductor laser frequency noise

设置调制频率为100 kHz，分别使激光器工作在3 kHz、100 kHz、200 kHz线宽下，对谐振式光纤陀螺进行调制解调实验，实验结果如图7所示。

图7 不同激光线宽下的谐振腔解调线测试结果Fig.7 The test results of resonant cavity demodulation line under different laser line widths

在每个线宽的实验中均采集12组解调曲线图像，计算每组测试曲线的斜率，并取12组平均值作为当前线宽下的解调曲线斜率。由此可以得到当激光器线宽分别为3 kHz、100 kHz、200 kHz时，谐振腔解调曲线的斜率分别为130 V/Hz、79 V/Hz、56 V/Hz（12组数据的平均值）。计算可得，激光器线宽100 kHz时的斜率值比3 kHz时降低了39.2%，200 kHz时的斜率值比3 kHz时降低了56.9%。在图5的仿真结果中，激光器线宽100 kHz时的斜率值比3 kHz时降低37.7%，200 kHz时的斜率值比3 kHz时降低59.8%。实际测得的解调曲线结果与理论仿真结果的对比分析如表1所示。

表1 谐振腔解调曲线斜率的理论值与试验值对比分析结果Tab.1 The comparison between the theoretical value and the experimental value of the slop of the demodulation cyrve

由上述分析可以看出，实验结果和理论仿真结果基本吻合。因此对于半高宽为300 kHz的光纤谐振腔，图5中激光器线宽与谐振腔解调曲线斜率的关系曲线图得到验证，是正确的，从而进一步得出应将激光器的线宽控制在3 kHz以内，才能保证标度因数偏离理想状态的程度不超过1%的结论。

4 结 论

在谐振式光纤陀螺中，激光光源并不是理想的单频光，不同程度的线宽展宽会导致陀螺的标度因数降低。本文通过研究激光器线宽对谐振腔透射端解调曲线斜率的影响，得到了陀螺标度因数变化与激光器线宽的关系。对于半高宽为300 kHz的光纤谐振腔，当半导体激光器线宽在3 kHz以内时，陀螺谐振腔透射端解调曲线斜率与理想状态时相差1%以内，也即陀螺标度因数因受激光器线宽影响而产生的变化不会超过1%。此外，针对不同半高全宽、不同清晰度的谐振腔，为满足更加理想的标度因数变化范围，应再以本文理论公式为基础进行进一步推导研究。