加速度计参数长期稳定性多尺度混合建模与预测

王晓东，付红坡，温云同

（北京航天控制仪器研究所，北京 100039）

石英挠性加速度计（以下称加速度计）因其体积小、响应快、灵敏度高等优点，在我国航空航天、国防军事等众多领域得到了广泛应用。作为惯性导航系统(INS)的关键敏感器件之一，加速度计的性能直接影响到INS的最终导航精度。由于加速度计受加工与制造过程中存在的残余应力释放、材料退化效应及外界环境载荷等因素的影响，它的零偏K0与标度因数K1等参数会发生变化[2]。目前应对加速度计参数变化的方法是定期对加速度计标定，但是长时间多次重复标定耗时耗力，造成其在使用过程中长期稳定性差、使用维护复杂，严重影响武器系统的使用维护性及效能的发挥。因此深入研究加速度计参数长期稳定性的规律具有很重要的意义。

对于加速度计参数长期稳定性规律的研究早已开始，主要有自回归滑动平均（ARMA）模型[1]、神经网络[2]、最小二乘向量机（Least Square Support Vector Method,LSSVM）[3]等方法。而经过试验研究表明，由于存在各种影响因素，加速度计参数的长期变化序列表现为典型非平稳、非线性的时间序列，包含多种复杂成分，因而单一的采用上面几种方法进行建模时拟合效果较差、模型预测精度低。因此如果先对参数变化序列进行预处理，将包含多种成分的参数变化序列分解为若干个规律性较强的子时间序列分量，并针对其特性选择适当的数学工具建模，通过预测子序列使预测风险分散化，则能够进一步提高预测精度。其中预处理方法有小波分解(Wavelet Decomposition,WD)、经验模态分解(Empirical Modal Decomposition,EMD)[4-5]等。

经验模态分解是一种基于信号局部特征的信号分解新方法，该方法不但具有小波变换的多分辨的优点，而且还能够进行自适应频率分析，因此更加适用于非线性、非平稳的时间序列分析[6]。为了弥补神经网络预测时较差的泛化能力与向量机拟合功能单一的缺陷，本文将多核最小二乘向量机（Multiple Kernel Least Square Support Vector Machine,MKLSSVM）算法[7-8]用于加速度计参数长期稳定性建模，根据不同的子序列特性构造组合核函数，充分挖掘各子时间序列的变化规律。由于MKLSSVM的性能很大程度上依赖于向量机参数的选取，而人工选取参数具有盲目性与主观性，所以设计一种自适应人工鱼群算法（Adaptive Artificial Fish Swarm Algorithm,AAFSA）对多核向量机参数进行寻优。

综上，本文提出一种基于经验模态分解与自适应人工鱼群优化多核最小二乘支持向量机的加速度计参数长期稳定性多尺度混合建模与预测方法。首先研究了使用EMD方法后各子序列的信号复杂度(排列熵)与拟合精度的关系，并比较了普通方法与多尺度分解方法的拟合精度；其次使用AFFSA方法对MKLSSVM的关键参数进行寻优；然后设计基于EMD与AAFSA优化MKLSSVM的参数长期稳定性模型；最后进行模型适用性验证与预测性能验证，并进行结果分析。

1 数据预处理

加速度计在存储及使用的过程中，加速度计参数变化序列包含多种复杂成分，如果不对其进行处理直接对其进行建模会导致拟合效果差、模型预测精度低。为了避免这种情况，本文采用经验模态分解(EMD)方法对参数长期变化序列进行预处理。

EMD方法假设任何复杂的时间信号都是由一系列简单且相互独立的固有模态函数(IMF)组成，而且每一个IMF分量必须满足：在整个序列数据段内，极值点数必须和过零点数一致或者至多相差一个；在任何一点，由极大值确定的上包络线和极小值确定的下包络线的均值为零。EMD方法的本质就是通过特征时间尺度获得IMF，然后由IMF来分解时间序列数据[8]。

为验证EMD方法的有效性，本节进行了两方面的研究：1）计算经过经验模态分解后各IMF分量的信号复杂度的变化，以及经过最小二乘支持向量机(LSSVM)拟合后各IMF分量的拟合精度的变化；2）比较不同多尺度方法和非多尺度方法的拟合效果。

选取某型石英挠性加速度计K0数据作为研究对象，使用EMD对该时间序列进行信号分解，得到图1所示的IMF序列波形。由图1可知从IMF1到IMF4，信号的复杂度一直在下降。

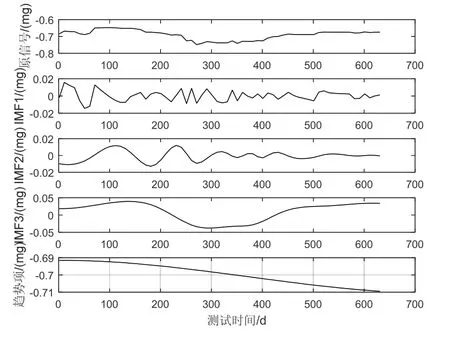
图1 K0变化的EMD分解Fig.1 The EMD decomposition of change of K0

选取排列熵作为评价信号复杂度的工具，并且用最小二乘向量机算法(LSSVM)对各IMF分量进行拟合，计算各分量拟合的均方差(MSE)。各IMF分量排列熵与拟合的误差如图2所示。由图2可知，随着分解阶数的增加，IMF信号的排列熵呈现出几乎线性化降低的趋势。而且拟合误差也快速下降。

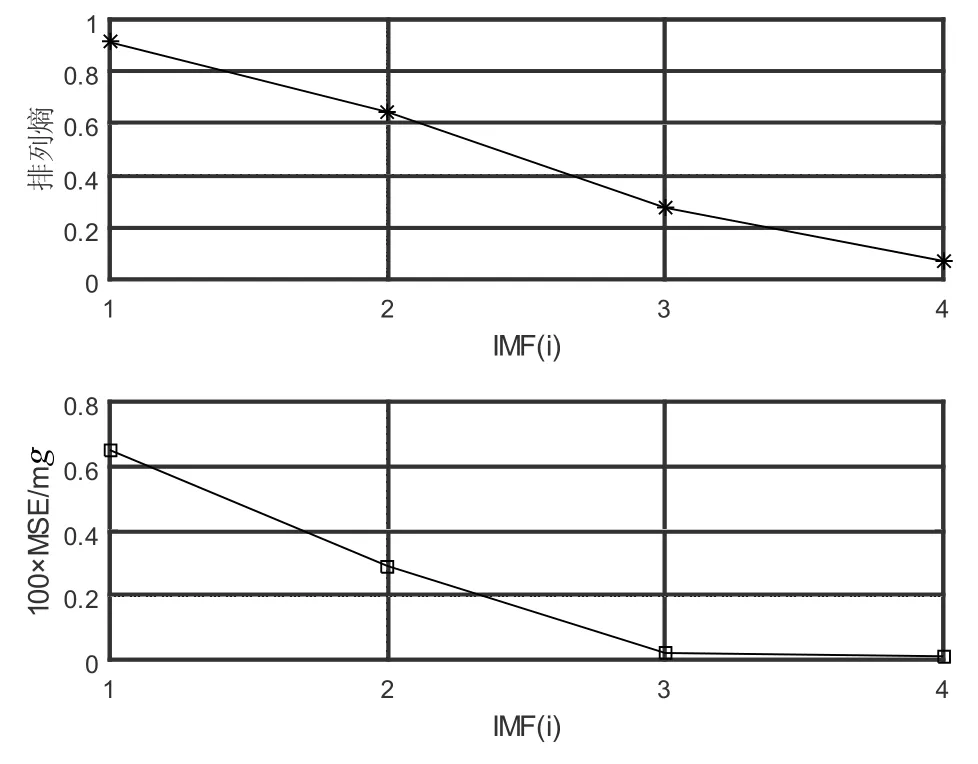
图2 IMF信号排列熵与LSSVM拟合各IMF的MSE误差Fig.2 Permutation entropy of IMF and MSE of LSSVM regression of IMF

为了比较多尺度和非多尺度方法的拟合效果，用LSSVM结合非多尺度、EMD、集合经验模态分解（EEMD）、多元经验模态分解（MEMD）四种方法对上述时间序列进行拟合，拟合误差结果如图3所示。由图3可知，多尺度分解可以大幅提升加速度计K0变化的拟合精度，而且其中EMD在各方面效果最好。

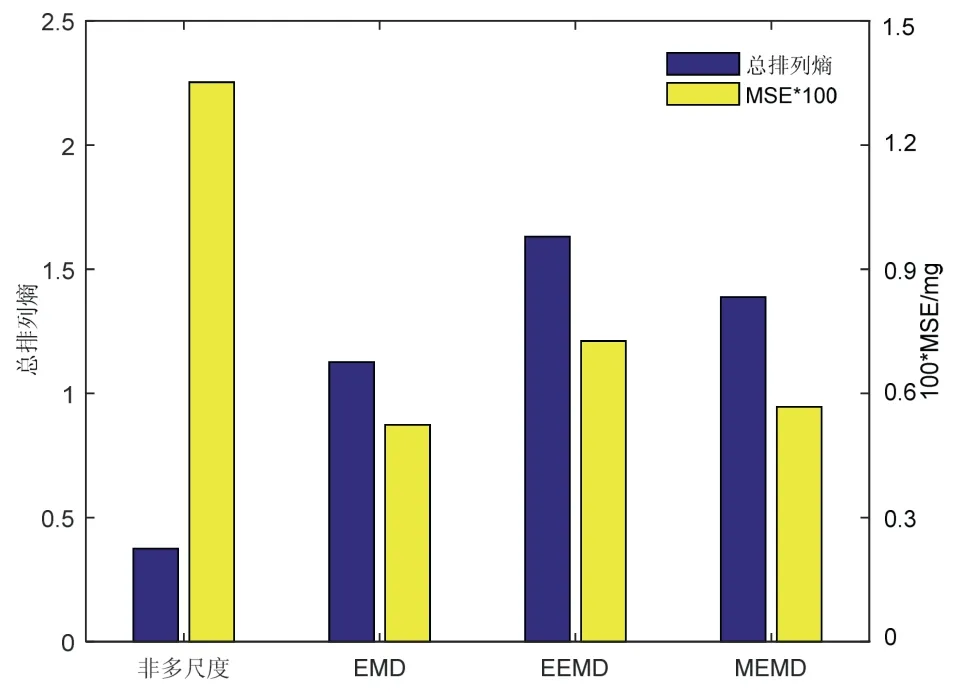
图3 不同数据拟合算法的熵及MSE对比Fig.3 Comparison on date entropies and MSE by different regression algorithms

上述分析表明，多尺度分解可以大幅提升加速度计参数变化序列的拟合精度，而且在几种多尺度分解方法中，EMD方法效果最好，因此本文选择EMD作为加速度参数长期变化序列预处理的工具。

2 改进多核最小二乘支持向量机（MKLSSVM）建模

2.1 模型建立

在本文中，根据时间变化与加速度计参数变化的对应关系，选定MKLSSVM模型训练样本为D∈RN×R，R为实数，i=1,2…N，N为样本个数。根据多核学习思想，等价核函数将RN映射到高维特征空间，然后建立回归拟合函数：

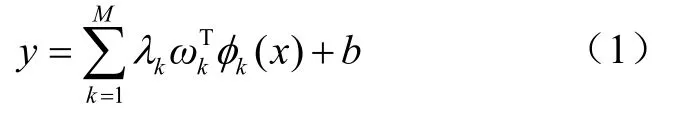
其中，φk(x)为输入样本映射到高维空间的非线性变化，λk为其系数，ωk为其权重，k= 1,2…M,M为核函数个数，b为常值偏差。由结构风险最小化原则将式(1)转化为以下最小值优化问题：

其中，C为惩罚系数，εi为第i个加速度计参数实际数据与期望数据的残差。采用拉格朗日方法建立式(3)所示的目标函数的拉格朗日函数：

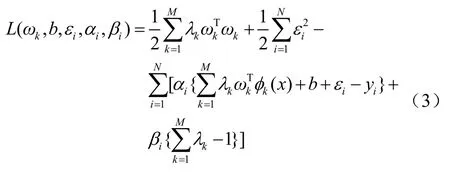
其中，αi,βi为拉格朗日因子。根据KKT条件，对式（3）所示的函数中的各变量求偏导，可得到用矩阵表示的y：

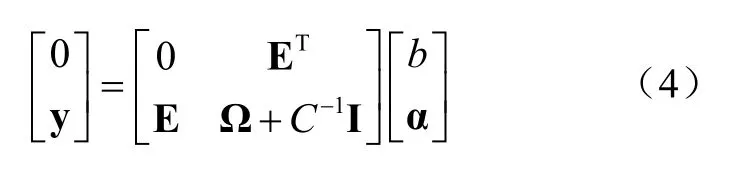
其中，y= [y1,y2,……,yN]T，E =[1,1,…1 ]T，α= [α1,α2…αN]T。Ω是 一 个N维对称矩阵，是满足条件的核函数，φk(xi)、φk(xj)分别 是第i与j个输入映射到高维空间的非线性变化，式中i,j= 1,2,……,N。

由最小二乘算法可求得b,α的表达式：

综合以上各表达式，求得加速度计参数长期稳定性模型为：

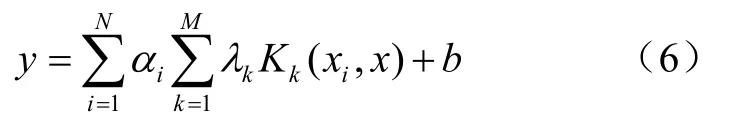
根据文献[9]可知，核函数的选取和惩罚系数及核函数参数的确定具有重要作用。由于不同时间段时间序列的变化特性不一样，而且不同的IMF分量的信号特征也不一样，同时每一个核函数的函数特性也不一样，因此在考虑核函数特性、加速度计参数变化序列的数据特性、算法复杂程度的基础上，本文选取三阶多项式核函数、指数型核函数、改进高斯径向基核函数进行加权组合构成等价核函数[10]。三种核函数表达式如下：

其中，c为多项式核函数参数；σ是指数型核函数参数；z是改进型高斯核函数的位移参数，μ为其核参数；将三种核函数表达式代入式(6)，则基于MKLSSVM的加速度计参数长期稳定性模型为：

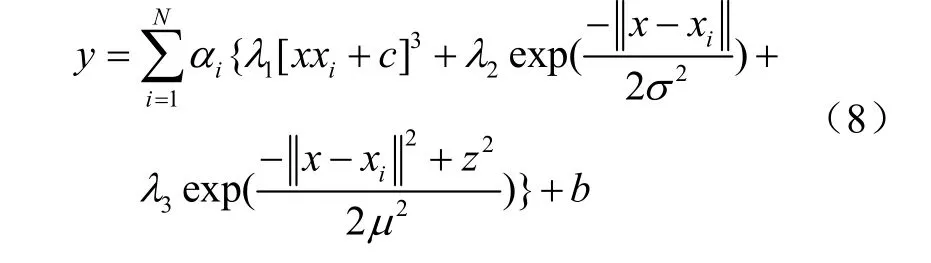
上述模型中λ3= 1-λ1-λ2。

2.2 模型参数确定

由2.1节所建立模型可知，模型精度直接受到C、c、σ、z和μ还有系数λ1，λ2等7个参数的影响，而如果

人为确定这些参数会受到主观因素的影响，模型有较大误差。通过分析文献资料与试验确定，人工鱼群算法在多参数同时寻优应用中表现优秀，因此本文选择采用人工鱼群算法[11]来对这些参数进行寻优，以期得到最优的模型参数。

人工鱼群算法一种智能优化算法[9-10]，在优化过程中，将每一只人工鱼设定为函数的一个可能最优解P，人工鱼的视野范围(Visual)看作解空间，视野范围内的食物浓度看作目标函数Q=f(P)，人工鱼朝着视野范围内食物浓度最高的位置游动来实现函数全局寻优[12]。

尽管人工鱼群算法具有寻优能力强、适应性好等特点，但是经过测试发现固定的人工鱼视野与步长会导致算法在寻优后期搜索能力变弱，易陷入局部最优，解精度不高，而且计算量会逐渐变大的情况[13-14]，因此对此做出改进。

(a)引入自适应衰减函数

经过分析可知，寻优过程前期希望人工鱼有较大的视野和步长可以快速收敛并且避免陷入局部最优，后期希望较小的视野和步长可以进行精确搜索，提高目标函数解的精度。因此，决定在固定视野与步长中引入一个衰减函数，在寻优过程中该函数能按设定的自适应函数系数的区间，根据算法不同阶段自适应地改变视野和步长的大小，如式(9)所示。

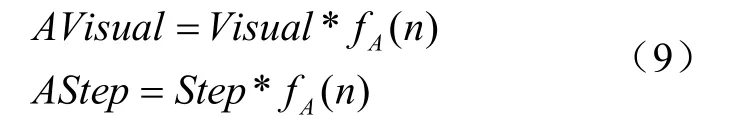
其中，AVisual为自适应人工鱼视野，Visual为人工鱼初始视野，AStep是自适应人工鱼步长，Step为人工鱼初始步长，n为寻优迭代次数，fA(n)为自适应衰减函数。

选定指数型函数为自适应衰减函数，该函数大趋势衰减，衰减的快慢由相关参数控制，自适应衰减函数表达式：

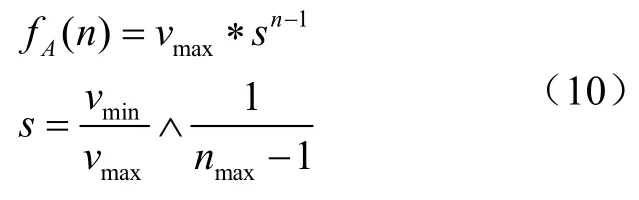
其中，n是当前迭代次数，v是自适应函数系数，定义其值域为 [vmin,vmax]，第一次迭代时函数系数的初始值为vmax，最后一次迭代的函数系数值为vmin，nmax是最大迭代次数。

(b)增加进化机制

随着迭代次数增加，鱼群算法的计算量会大幅增加而影响收敛速度，为了应对这一问题引入“适者生存”的进化机制。在迭代次数到达最大迭代次数的一半之后，每次迭代之后对人工鱼群按照适应度的大小进行排序，选择一定比例的适应度较低的人工鱼视为劣化个体，然后进行淘汰以减少空间占有量。但为了防止鱼群的多样性减少，设定当鱼群数目少于鱼群总数的一半时停止淘汰，保持人工鱼群种类的多样性，防止陷入局部极值。

将人工鱼群算法与MKLSSVM进行结合，本文建立改进MKLSSVM模型。

3 基于EMD与改进MKLSSVM的加速度计参数长期稳定性建模

3.1 建模过程

加速度计参数长期稳定性建模过程如下：

步骤1：原始数据获取。从加速度计数据管理系统中导出某型号加速度计参数变化序列。

步骤2：数据预处理。用EMD对原始参数变化序列进行分解，得到各IMF分量，分别作为MKLSSVM的训练样本。

步骤3：参数初始化。确定鱼群的各个初始参数并确定待优化参数（C,c,σ,μ,z,λ1,λ2）的取值范围。根据待优化参数的取值范围对每条人工鱼随机初始化，并设定鱼群算法的适应度是训练数据的均方根误差。

步骤4：寻优计算。人工鱼分段自适应调节步长与视野，执行全局寻优行为。满足停止条件后输出最优参数，否则继续执行寻优操作。

步骤5：建立模型。寻优结束将最优参数代入MKLSSVM，用训练样本对向量机进行训练，建立加速度计参数长期稳定性模型，对各个分量的预测结果进行等权求和集成为综合预测结果。

步骤6：模型验证。选取同一型号加速度计参数变化序列作为测试样本进行模型测试，并对参数进行预测。将结果与实际值进行对比分析。

基于EMD与改进MKLSSVM的加速度计参数长期稳定性模型结构如图4所示。

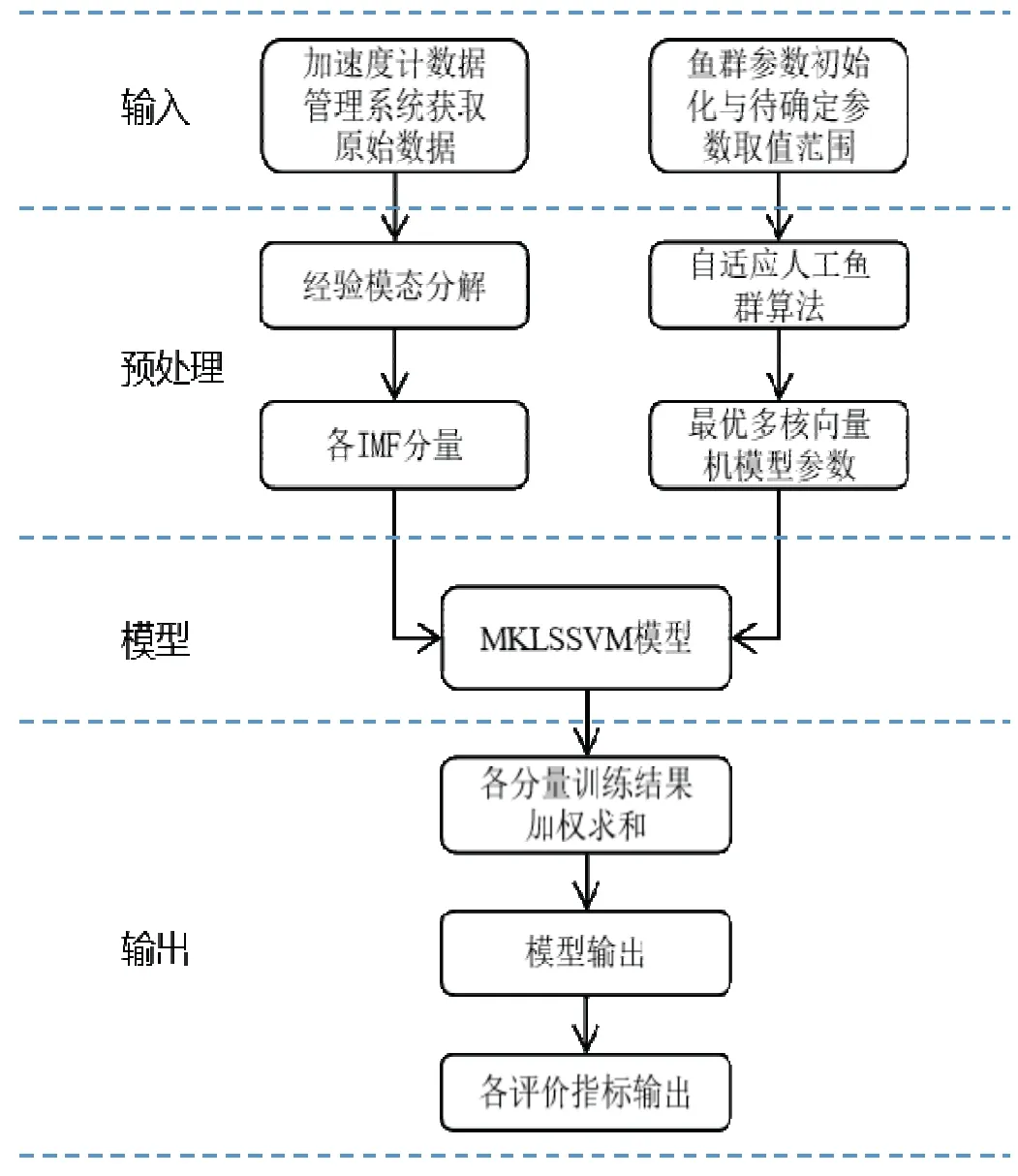
图4 加速度计参数长期稳定性模型结构Fig.4 The model structure of long-term stability of accelerometer parameters

3.2 模型评价指标

选择三种指标来评估模型的拟合与预测效果，分别为最大绝对误差（MAXE）、平均绝对误差（MAPE）、均方根误差（RMSE）。三种评价指标的计算如式(11)：

其中，y(i)为实际值，为模型输出值。

4 模型验证

人工鱼群初始参数如下：人工鱼数目S= 50，视野Visual = 6，步长Step = 1，拥挤度因子δ= 0.618，最大尝试次数W= 30,最大迭代次数nmax= 100，自适应函数v取值范围[0.1,2]；待优化参数范围：惩罚系数C为50～200、指数型核函数参数σ、改进高斯型径向基核函数参数μ为0.01～20，多项式核函数参数c、位移z为0.01～10，核函数系数为0～0.5。

选取某型号加速度计将近 600 天的稳定性测试数据为原始样本数据。数据测试方法为 1g条件下四位置翻滚测试；测试设备为石英挠性加速度计大型自动化测试设备；数据采集设备是安捷伦 3458A 高精度数字电压表，分辨率为8位半，电压基准稳定度每年8 ppm(选件 4 ppm)。

4.1 模型适用性验证

4.1.1 基于EMD的参数变化预处理

选取的加速度计的零偏K0与标度因数K1的600 天内的变化情况如图5所示。

图5 选取的加速度计参数变化序列Fig.5 Parameter change sequence of selected accelerometer

分别对K0与K1变化序列进行经验模态分解，逐级分理出相应的3个IMF分量与一个趋势项。分解结果如图6所示。

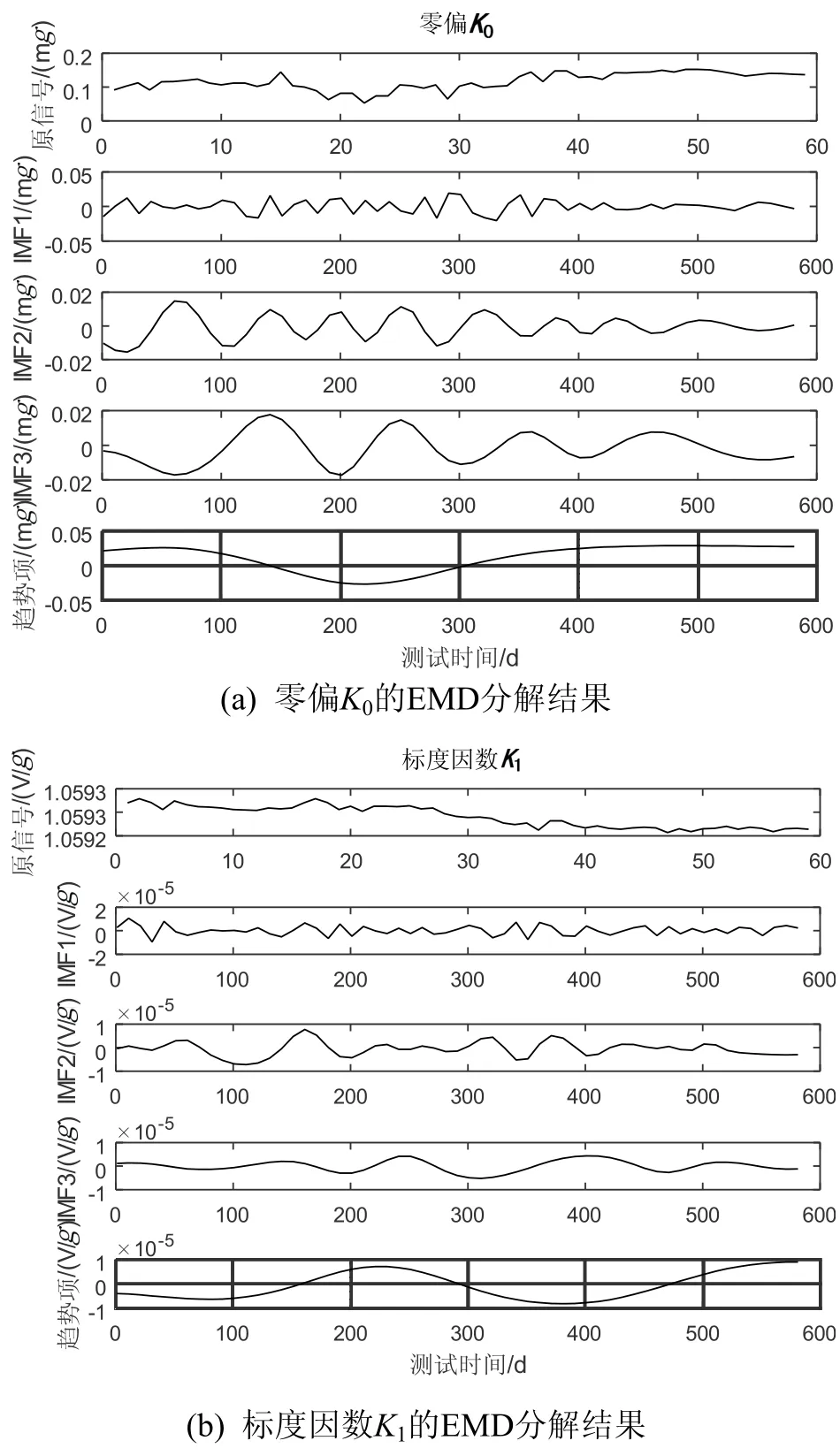
图6 零偏K0与标度因数K1的EMD分解结果Fig.6 The results of EMD decomposition of K0and K1

4.1.2 模型适用性验证与结果分析

验证加速度计参数长期稳定性模型的主要步骤为三步：首先，进行LSSVM模型与MKLSSVM模型在参数变化拟合训练中的精度对比，以验证MKLSSVM在参数变化建模问题中的优势；其次，在MKLSSVM模型的基础上使用人工鱼群算法对其关键参数进行寻优，验证人工鱼群优化MKLSSVM模型参数后建模精度更高，模型性能更好；最后，采用EMD方法与优化MKLSSVM模型结合应用，并与前两步进行对比，以验证序列平稳化处理能够有效提升参数变化建模的精度与预测性能。

用4种模型分别对K0与K1长期变化序列进行拟合，各模型拟合结果如图7所示，模型的拟合误差情况如图8所示。

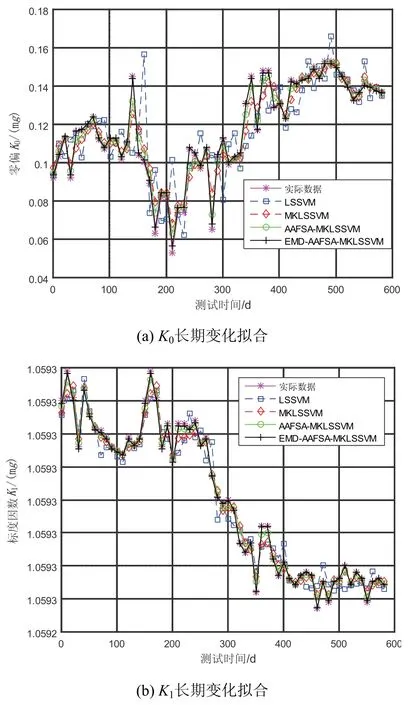
图7 加速度计参数长期变化拟合Fig.7 The fitting of the long-term variation of accelerometer parameters

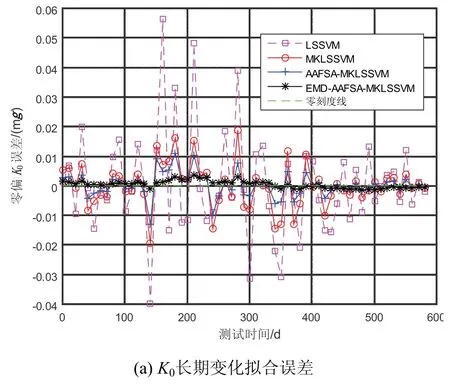
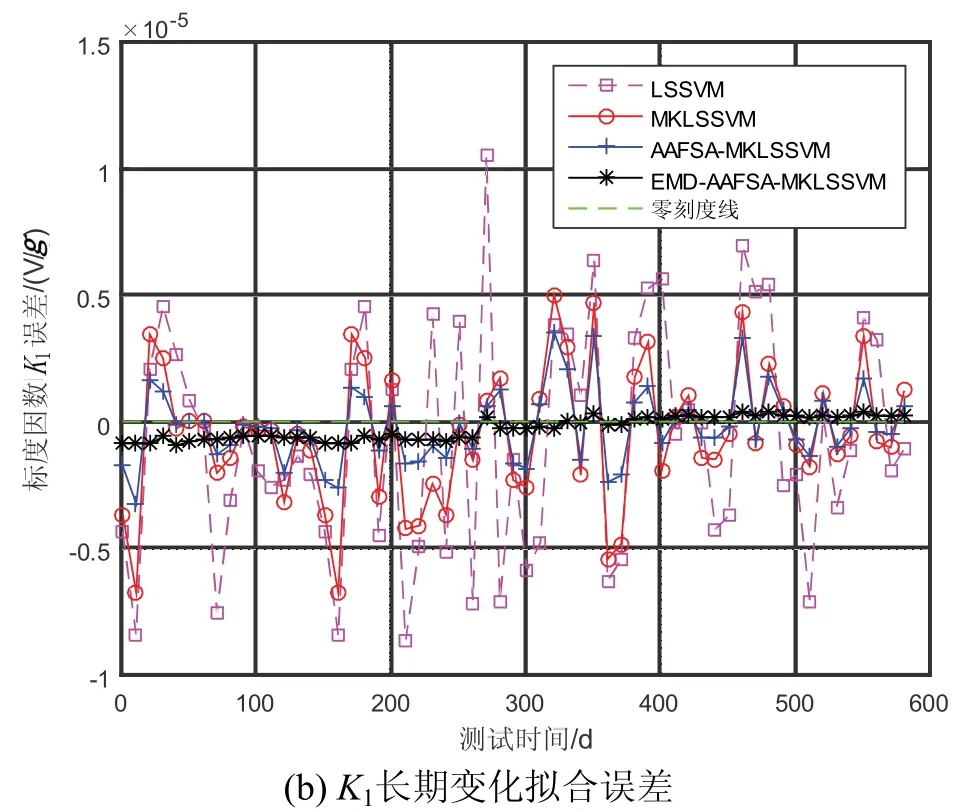
图8 加速度计参数长期变化拟合误差Fig.8 The fitting residual of the long-term variation of accelerometer parameters

由图7可知，训练结果表明4种模型对加速度计的K0与K1变化都能够较好地拟合，但相比于LSSVM、MKLSSVM，在采用EMD进行数据预处理与AAFSA进行向量机参数寻优之后所建立的模型对原始参数曲线实现了更大程度上的拟合。

由图8可知，在4种模型的训练输出误差变化中，LSSVM模型误差变化范围较大，MKLSSVM模型误差变化范围减小，经过AAFSA优化后模型误差变化进一步减小，在加入基于EMD的参数变化预处理后，模型的误差变化范围更小而且很稳定。

对4种模型训练误差进一步分析，计算各模型评价指标，结果如表1所示。

表1 模型拟合效果评价指标Tab.1 The index of model fitting effect evaluation

对表1进行分析，相比于LSSVM模型，MKSSVM模型对于零偏K0与标度因数K1拟合的MAXE分别降低了31.12%、32.45%，MAPE分别降低了31.22%、32.46%，RMSE分别降低了43.41%、44.32%，再结合对图7、8的分析可知，相比于LSSVM，MKLSSVM模型能够更为有效地捕捉到加速度计参数长期稳定性的历史规律。

同时，对MKSSVM模型进行参数优化后，对于K0与K1拟合的MAXE分别降低了35.18%、34.61%，MAPE分别降低了39.33%、45.17%，RMSE分别降低了42.13%、43.22%，再结合对图7、8的分析可知，对MKLSSVM模型的参数利用AAFSA进行寻优可以提升模型的精度、降低参数变化拟合误差。

在优化MKSSVM模型的基础上对用EMD方法对参数变化序列进行预处理后，对于K0与K1的拟合的MAXE分别下降了42.53%、48.86%，MAPE指标分别下降了43.22%、41.04%，RMSE指标分别下降了42.97%、40.15%，再结合对图7、8的分析可知，利用EMD方法对加速度计参数长期变化序列的平稳化处理对模型精度的提升与参数变化的拟合效果起到很大的作用，说明了参数变化序列平稳化处理的必要性。而且K0与K1拟合的RMSE的值分别为2.21×10-3mg与0.73×10-6V/g，均达到了10-6(g)量级，符合实际的应用。

综上可知，本论文所建立的模型在MKLSSVM模型的基础上进行模型参数优化提升了对加速度计参数长期稳定性建模能力与精度的同时，运用EMD方法降低了参数变化序列的不平稳性与不同时间尺度信息间的相互影响，其MAXE、MAPE与MAPE指标数值均优于其他对比模型，表明本文所建模型相比于传统的加速度计参数长期稳定性模型误差更小、精度更高。为加速度计参数变化预测提供了一个精确的模型。

4.2 模型预测性能验证

利用4.1节中所训练好的4种模型，首先对各子序列分量进行单步预测，然后将单步预测的结果放入到历史参数变化数据中，将其变成相应的预测模型的新输入数据序列，通过这样的方式可实现各分量的多步滚动预测。进而叠加各子序列分量的多步预测结果。对加速度计的参数变化进行6次预测，并对预测结果进行分析。预测结果与实际结果对比如图9所示，预测误差情况如图10所示。

由图9可知，4种模型都能够对加速度计参数进行较准确的预测。但是相比于LSSVM、MKLSSVM与AAFSA-MKLSSVM三种模型，本文提出的方法所建模型对参数变化的预测与实际的参数变化情况最为贴近。

由图10可知，在4种模型的预测误差中，在对MKLSSVM模型进行参数寻优以及加入基于EMD参数序列预处理后，多步的预测误差变化范围非常小而且很稳定。

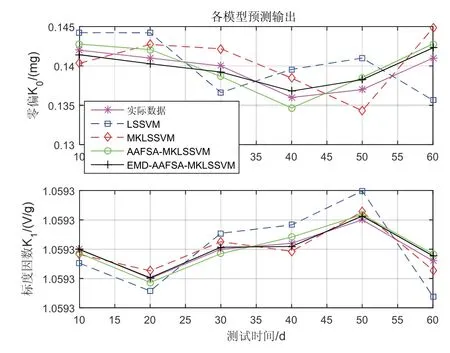
图9 加速度计参数变化多步预测Fig.9 The multi-step prediction of accelerometer parameter

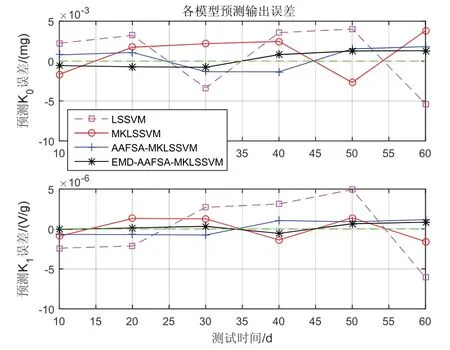
图10 加速度计参数变化多步预测误差Fig.10 The multi-step prediction residual of accelerometer parameter

对4种模型计算其输出的平均绝对误差（MAPE）与均方根误差（RMSE），K0与K1的各模型多步预测输出的误差计算值如表2所示。

表2 模型预测效果评价指标计算结果Tab.2 The calculation result of model prediction effect evaluation index

对表2中数据分析可知：由于误差积累效应导致各模型的误差随着预测步数的增加而上升；对K0的变化进行预测时，相比于LSSVM、MKLSSVM与AAFSA-MKLSSV模型，EMD+AAFSA-MKLSSVM模型在第6步预测时MAPE分别降低了84.69%、63.53%、40.92%；RMSE分别降低了88.65%、61.23%、43.35%。同样在K1的第6步预测时，MAPE分别降低了78.38%、57.44%、34.37%；RMSE分别降低了86.49%、61.55%、45.21%。而且 EMD+AAFSA-MKLSSVM 模型的每一步的预测误差均在10-6量级，符合实际应用的要求。

结合图9、10与表2，可知本文方法所建立的加速度计参数长期稳定性模型能够对加速度计参数的变化进行高精度的预测，而且相比于传统的预测模型预测均方根误差降低 85% 以上。

5 结 论

本文分析了经验模态分解与自适应人工鱼群算法优化多核最小二乘支持向量机在加速度计参数长期稳定性建模与预测中的应用，经过实例验证与对比分析，可以得到以下结论：

1）经过EMD数据预处理与AAFSA优化MKLSSVM 建立的模型，与一般的LSSVM相比，模型准确度更高，能显著提高加速度计K0与K1变化的预测精度。

2）该建模方法和传统的加速度计参数长期稳定性建模方法相比可以更加有效地补偿加速度计的参数变化误差，对提高载体惯性导航精度与稳定性有重大意义。

3）多核最小二乘支持向量机在参数预测尤其是在非线性时间序列预测方面优势明显。