基于线性矩阵不等式的离散系统集成故障估计与容错控制

戴洪德，罗鑫辉，常 波，戴邵武

（海军航空大学，山东烟台 264001）

随着控制系统的可靠性和安全性要求越来越高，故障诊断与容错控制已成为控制领域的一个重要分支[1,2]。故障诊断有两种方法：故障检测与隔离和故障估计。相比于故障检测与隔离，故障估计可以获得故障值，直接应用于容错控制，具有更广阔的应用前景，而且故障估计本质上包括了故障检测与隔离，因此，对系统进行故障估计与容错控制具有重要的理论研究意义和实际应用价值[3-5]。

在故障诊断与容错控制领域内，基于观测器的容错控制引起了学者的广泛关注，主要有滑模观测器（SMO）[6-8]，未知输入观测器（UIO）[9,10]，自适应观测器（AO）[11-13]等。Edwards首次提出等价输入的概念[6]，设计滑模观测器实现了对传感器故障的估计；胡正高等对于滑模观测器出现的颤振现象，提出了二阶滑模观测器实现了执行器故障估计[7]；随后在滑模观测器进行故障估计的基础上，Lan等设计容错控制器实现了涡轮桨距控制系统的容错控制[8]。但是滑模观测器需要满足观测器匹配的条件，而且需要知道故障的上下限。针对存在系统不确定性的马尔可夫跳跃系统[9]和T-S模糊系统模型[10]，Li等设计未知输入观测器对系统故障进行估计，然后根据得到的故障信息设计容错控制器，分两步设计观测器与容错控制器，实现了故障估计与容错控制的分离设计。针对线性离散系统的执行器故障，Jiang等提出了一种自适应观测器[11-12]，实现了故障估计与容错控制的分离设计；为了更好地对故障进行估计，在自适应观测器的基础上，Qian提出了一种降阶观测器[13]，实现执行器故障估计与容错控制。文献[8-13]根据观测器得到的故障估计值设计容错控制器，使得系统在故障状态下也能保持稳定并满足H∞性能指标，但是观测器和容错控制器是分离设计，而在闭环控制系统中存在系统状态和故障的误差项，使得系统观测器与容错控制之间存在耦合，为了实现解耦，文献[8-13]将闭环控制系统状态和故障误差项当作未知扰动，实现鲁棒控制。最近，Lan和Liu提出了一种新的集成设计方法[14-16]，建立误差方程与闭环控制系统的增广系统模型，一步设计观测器与容错控制器，实现集成故障估计与容错控制。但是，文献[14-16]都是针对连续系统进行研究，而对于离散系统的研究较少。一方面由于离散系统中双线性项的出现，离散系统的观测器和控制器设计要比连续系统困难，另一方面随着计算机应用于控制系统，离散系统的设计引起了广泛的关注。Nguyen虽然针对离散系统的观测器与控制器的集成设计进行了研究[17,18]，但是没有考虑系统存在故障的情况。另外，对于控制系统来说，模型误差和系统扰动是不可避免的，而文献[8-13]没有考虑到系统的模型误差。

基于以上分析，本文针对存在系统不确定性、未知扰动以及执行器故障的离散系统，进行集成故障估计与容错控制。首先，对于故障估计与容错控制之间存在的耦合，建立系统误差方程与闭环控制系统的增广系统模型。然后，利用D-稳定引理与H∞控制对增广系统设计，实现多性能约束条件下的集成故障估计与容错控制。最后利用所提的方法开展仿真实验，实现了飞行控制系统在不同故障条件下的集成故障估计与容错控制。

1 问题描述

考虑如下存在系统不确定性、未知干扰以及执行器故障的离散系统：

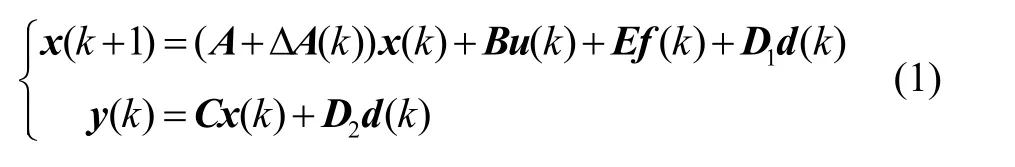
其中x(k)∈Rn、y(k)∈Rm和u(k)∈Rl分别为系统的状态、输出和控制输入，d(k)∈Rp为系统未知干扰，f(k)∈Rq为执行器故障向量，A∈Rn×n、B∈Rn×l、C∈Rm×n和E∈Rn×q为 系 数 矩 阵，D1∈Rn×p和D2∈Rm×p为扰动矩阵，ΔA(k)∈Rn×n为系统存在的不确定性。

在下文中，将对系统(1)的故障估计与容错控制集成设计问题进行研究，为了解决这个问题，给出如下假设和引理。

假设1：矩阵(A,C)完全可观的，矩阵(A,B)完全可控的。

假设2：rank(B,E)=rank(B)=l。

假设3：系统的不确定性 ΔA(k)是有界的，形式如下

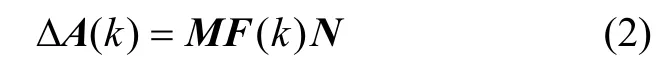
其中，M∈Rn×n、N∈Rn×n为已知矩阵，F(k)满足不等式FT(k)F(k)≤I。

引理1：（圆盘引理）[19]对于给定的圆盘区域D(α,r)（α为圆盘中心，r为圆盘半径）以及正定矩阵P、矩阵A，如果不等式

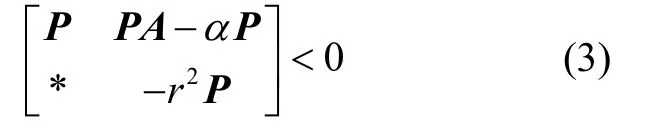
成立，则矩阵A的特征值位于圆盘区域D(α,r)内。

引理2：（Young不等式）[20]对于合适维度的矩阵M,N,F(k)以及常数ε＞ 0,满足FT(k)F(k)≤I，则不等式

成立，其中He(*)=（*）+（*）T。

引理3：（Schur补引理）[21]对于对称矩阵，下列条件是等价的：

（1）S＜0；

注1：利用引理1和H∞控制理论对系统进行设计，会得到非线性不等式，但是直接求解比较困难，因此需要利用引理2和引理3对非线性不等式进行简化，得到易求解的线性矩阵不等式。

2 故障估计与容错控制集成设计

2.1 故障观测器设计

为了对系统的状态和故障进行估计，设计如下故障观测器：

其中L、G为故障观测器待设计的增益矩阵。

系统状态和故障估计误差定义如下：

则由式(1)(5)(6)得系统的误差方程为：

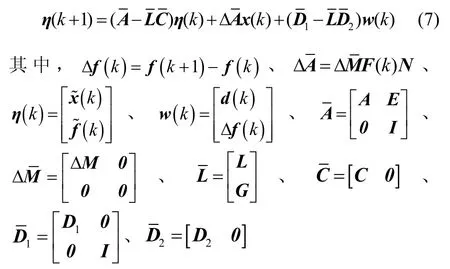
注2对于误差方程式(7)，要想故障观测器存在，则矩阵（A,E,C）不存在位于1的不变零点[12]，而对于一般的自适应观测器需要满足严格等式约束即SPR条件[13]：（1）rank（CE）=q，（2）矩阵（A,E,C）不存在位于1的不变零点。

2.2 容错控制器设计

针对系统式(1)，设计如下容错控制器：

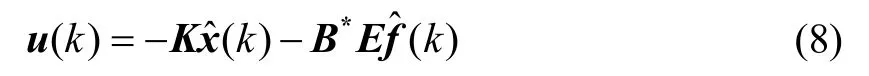
其中，K为待设计的增益矩阵，B*=(BTB)-1BT为矩阵B的广义逆矩阵。

将式(8)代入系统式(1)，则闭环控制系统方程为

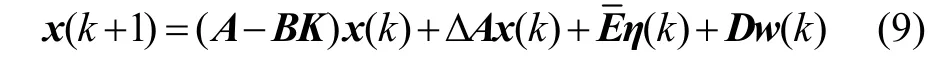
对于闭环控制系统(9)，在文献[11]进行分离设计时，将误差项当作未知干扰，通过设计增益矩阵K，使得闭环控制系统保持稳定且满足H∞性能||η(k)||∞＜γ2||w(k)||∞。但是实际上闭环控制系统式(9)与系统状态和故障估计误差η（k）存在耦合，而在设计增益矩阵K时，如果不考虑估计误差η（k）的影响，那么系统状态出现较大误差。所以考虑到误差方程式(7)和闭环控制系统式(9)两者存在的耦合，对系统式(7)和式(9)进行集成设计，减少两者耦合造成的误差。

2.3 集成设计

系统的误差方程和闭环控制系统的增广系统模型如下：

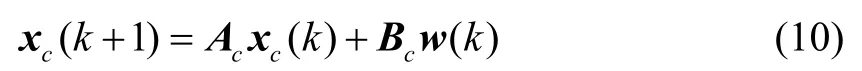
其中

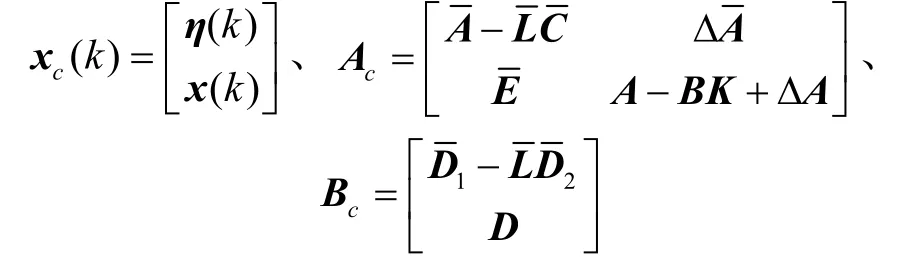
定理1：如果存在对称正定矩阵P∈R(n+q)×(n+q)和Q∈Rn×n，矩阵X∈R(n+q)×m和Z∈Rl×n，对于给定的圆盘D(α,r)，常数εi（i= 1,2,3）满足下列不等式

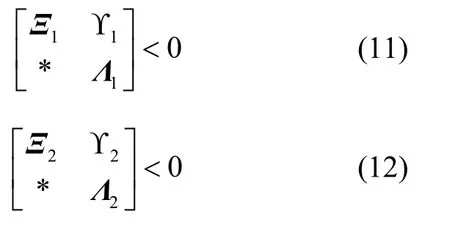
其中，

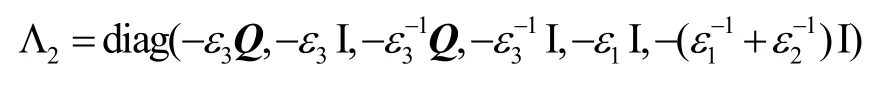
那么系统满足H∞性能||η(k)||∞＜γ||w(k)||∞，矩阵Ac的特征值位于圆盘D(α,r)内，增益矩阵=P-1X和K=ZQ-1。

证明：定义Lyapunov函数V(k)=xcT(k)Πxc(k)，其中，Π=diag(P,Q-1)，P∈R(n+q)×(n+q)和Q∈Rn×n为正定对称矩阵。定义矩阵

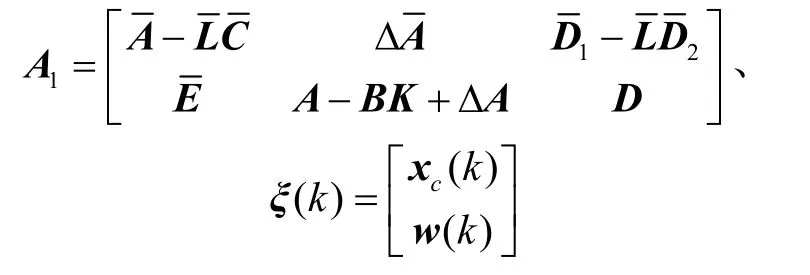
则

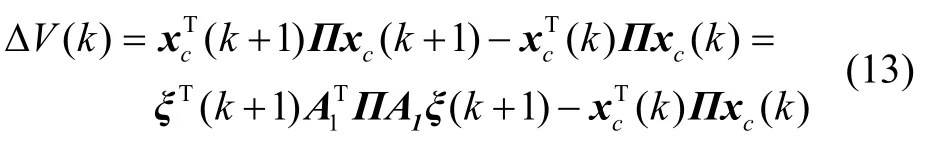
要想系统方程式(10)满足H∞性能||η(k)||∞＜γ||w(k)||∞，则

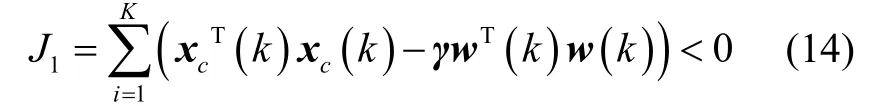
在零初始条件V(0)= 0下，

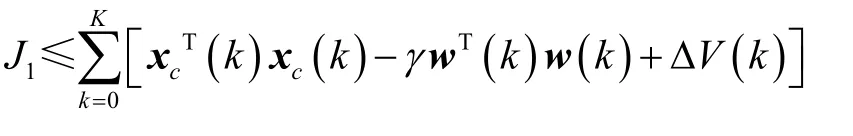
所以，式(14)成立的充分条件为

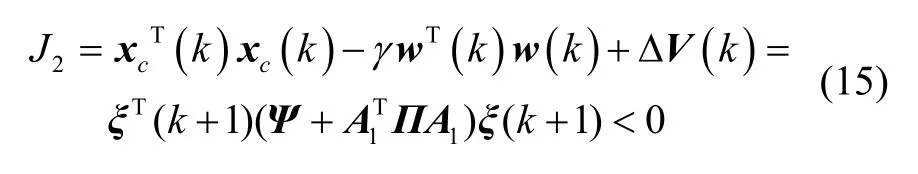
其中 Ψ=diag（I-PI-Q-1-γI）

根据引理3，Ψ+A1TΠΠ-1ΠA1＜0等价于

在式(16)两边同时乘以diag(I,Q,I,Q,I)，得

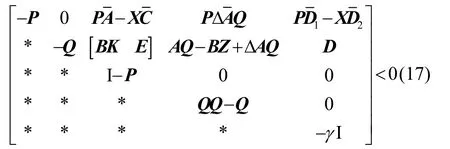
其中，X=PL和Z=KQ。

由于式(17)中含有BK、、ΔAQ和QQ项，使得不等式(17)求解非常困难，为了得到易求解的线性矩阵不等式，下面将对不等式(17)进行处理。定义

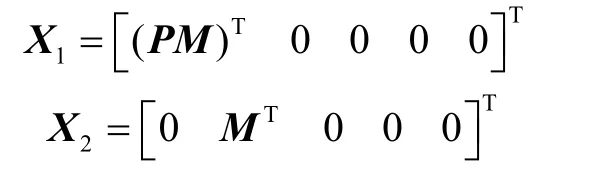
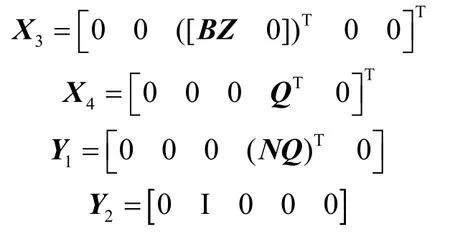
式(17)等价于

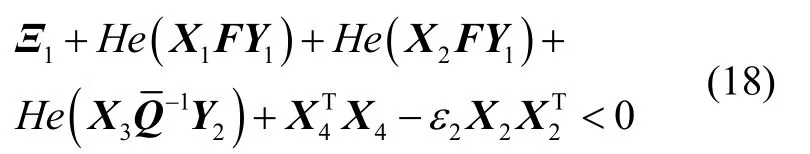
其中=diag(Q,I)。

由引理2得，

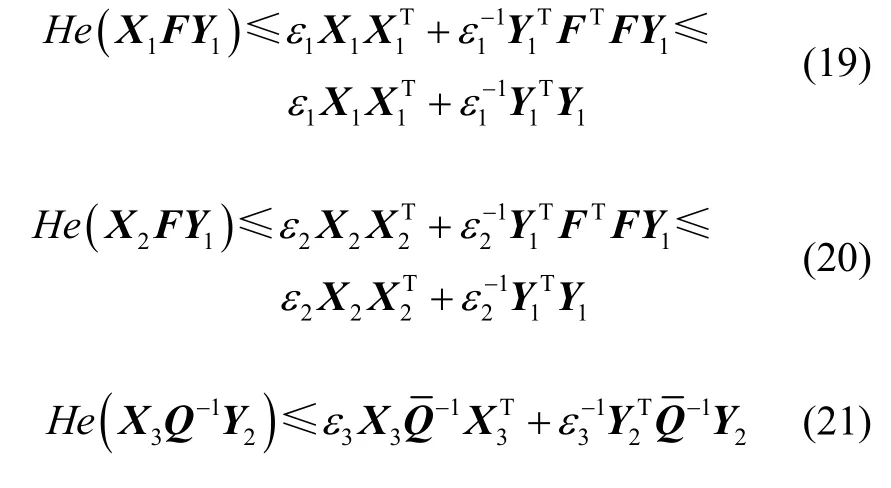
式(18)成立的充分条件为

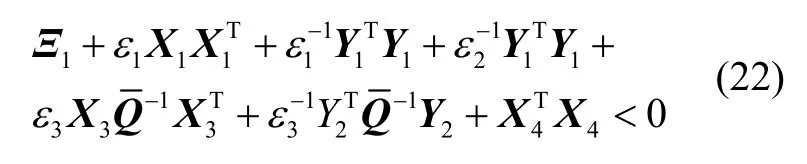
根据引理3可得不等式(11)，所以如果不等式(11)成立，则系统满足H∞性能||η(k)||∞＜γ||w(k)||∞。

由引理1可知，矩阵Ac的特征值要位于圆盘区域D（α,r），则存在对称正定矩阵，满足不等式：

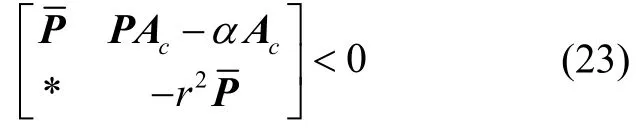
令=diag(P,Q-1)，在式(23)左右两边同时乘以diag(I,Q,I,Q)，得

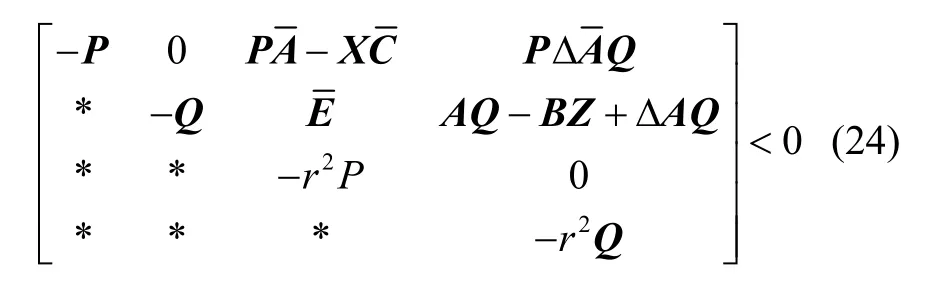
由于式(24)中含有和ΔAQ项，使得不等式求解非常困难，为了得到易求解的线性矩阵不等式，下面将对不等式(24)进行处理。定义

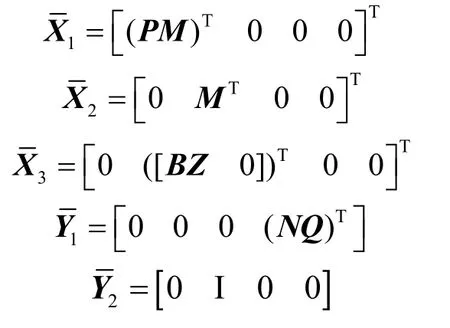
式(24)等价于

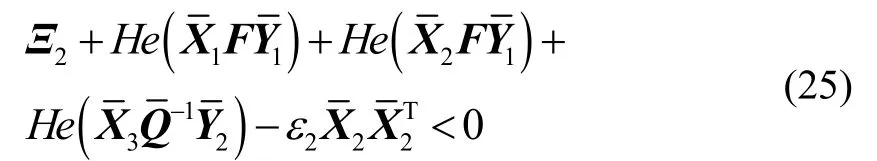
由引理2得，

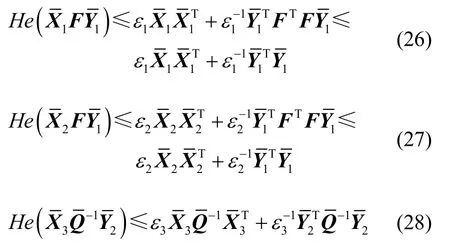
式(25)成立的充分条件为

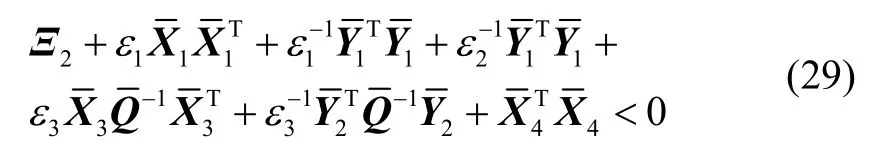
根据引理3可得式(12)，所以如果不等式(12)成立，那么矩阵Ac的特征值要位于圆盘区域D（α,r），定理1证明成立。

对于系统(10)，根据定理1集成设计增益矩阵和K，使得系统矩阵Ac的特征值位于圆盘D(α,r)内，系统满足H∞性能||η(k)||∞＜γ||w(k)||∞，实现多性能约束条件下的集成故障估计与容错控制。本文提出的算法如下所示：

Step1：根据故障观测器(5)(6)建立系统的误差方程式(7)，得到矩阵

Step2：根据容错控制器建立系统的闭环控制系统(9)，得到矩阵D。

Step3：根据定理1，解算出矩阵P、Q、Y、Z，并求得矩阵

Step4：根据定义B*=(BTB)-1BT，求出矩阵B*，该算法的控制框图如图1所示。

3 仿真验证

为了对本文提出的算法进行验证，下面将所提的方法应用于飞行控制系统的集成故障估计与容错控制中。本文以文献[22]给出的飞行控制系统模型作为研究对象，模型如式(30)所示。

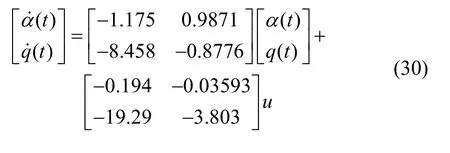
其中，α(t)和q(t)分别为飞机的攻角（°）和俯仰角速度（°/s），控制输入u为升降舵偏角（°）和推力（105N），对该模型进行离散化，离散时间为0.01 s，得离散化模型为：

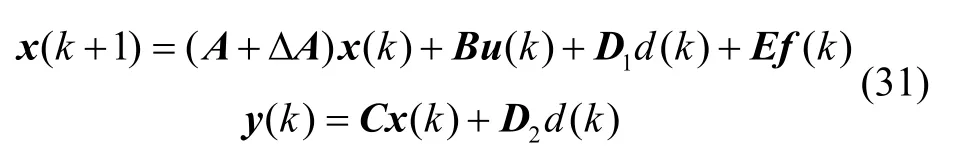
各系数矩阵为：

其中，x（k）=［α(k),q(k)］T，D1、D2为干扰矩阵，d(k)为干扰，E为故障矩阵，f(k)为执行器故障，ΔA为系统不确定性矩阵。

Step1：建立如式(7)所示的误差方程，得到矩阵

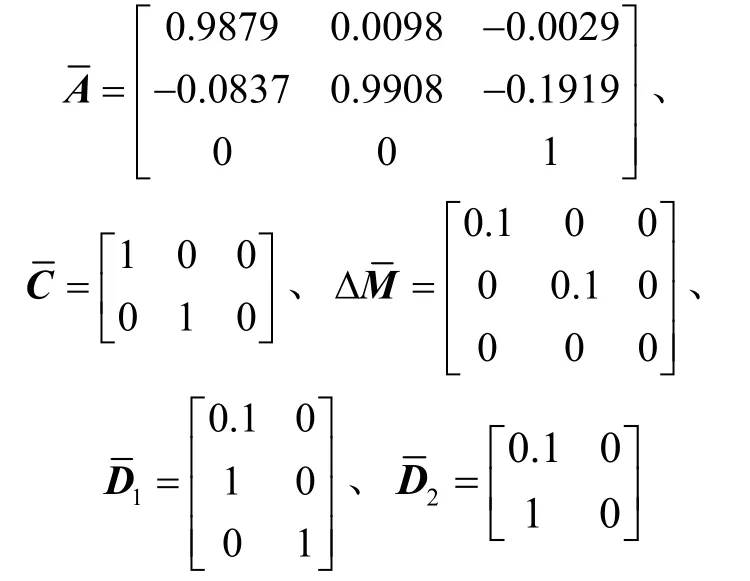
Step2：建立如式(9)所示的闭环控制系统方程，得到矩阵

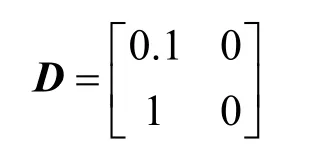
Step3：选择圆盘区域D( 0,0.95)，常数ε1= 0.2、ε2= 0.14、ε2= 2，以及H∞性能指标γ= 0.5，根据定理1，解算得

并求得系统故障观测器和容错控制器的增益矩阵如下：

Step4：根据定义B*=(BTB)-1BT求得

根据故障变化情况的不同，故障可以分为：突变故障、时变故障和间歇故障。为了更好地说明本文算法的收敛性，假设飞行控制系统的升降舵出现恒定偏差和时变偏差故障（单位为°），故障形式如下：

为了更好阐述本文所提出的集成故障估计与容错控制方法，将对本文所提的集成设计算法与文献[18]中的正常控制和文献[12]中的分离设计方法进行对比研究。其中文献[12]的分离设计方法见第2节式(7)和式(9)，在文献[18]中，不考虑系统存在执行器故障f(k)，设计的控制器与观测器如下：

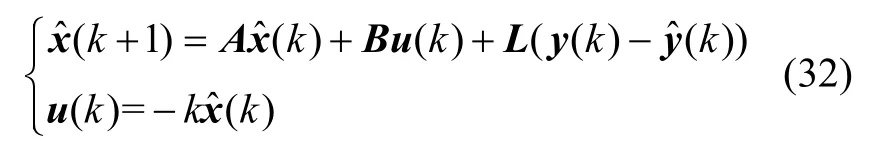
假设系统扰动d= 0.01sin(t)，根据设计的故障观测器和容错控制器参数，得到仿真结果如图2- 4，其中图2为故障估计误差曲线，图3和图4分别为系统攻角和俯仰角速度误差曲线。

图2 故障估计误差曲线Fig.2 The error curve of fault estimation

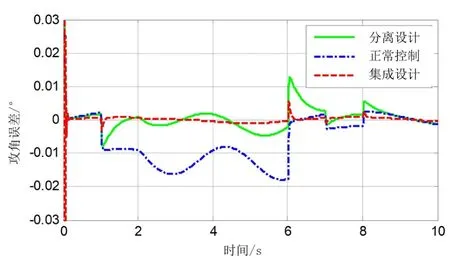
图3 攻角误差曲线Fig.3 The error curve of α( k)

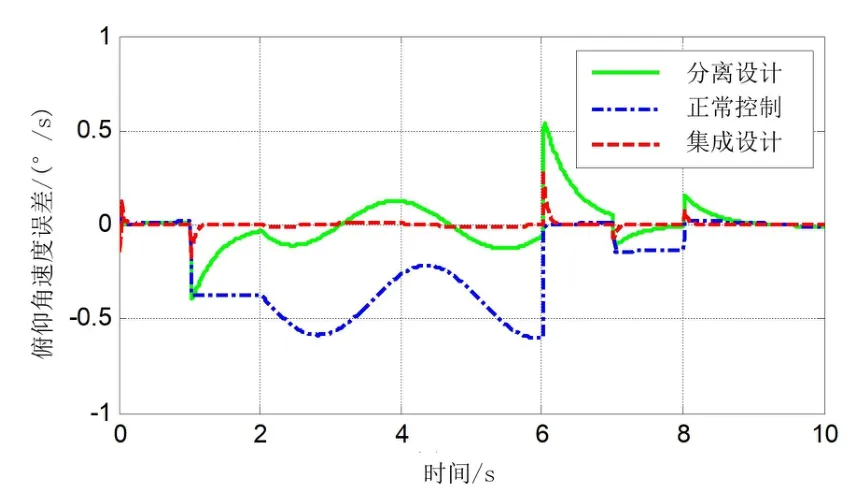
图4 俯仰角速度误差曲线Fig.4 The error curve of q(k)

由图2可知，文献[12]的分离设计和本文的集成设计方法都可以对发生的三种故障进行估计，但是本文提出的集成设计方法对故障估计的快速性更好、估计误差更小。当系统发生突变故障和间歇故障时，集成设计方法只需要0.3 s就可以对故障值进行估计，而文献[12]中分离设计方法需要1 s；估计速度提升70%；当系统出现时变故障时，集成设计方法故障估计误差幅值为0.1°，而文献中分离设计方法故障估计误差幅值为0.3°，估计误差减小66.7%。由图3和图4可知，当系统无升降舵故障时，三种设计方法中的攻角和俯仰角速度误差均趋近于0，而当系统出现故障时，正常控制作用下的系统输出误差明显增大，集成设计和分离设计方法下的系统输出误差仍然趋近于0，而集成设计方法的系统输出要优于分离设计方法的系统输出，误差更小。

4 结 论

本文针对存在不确定性、未知干扰和执行器故障的线性离散系统，提出了一种集成故障估计与容错控制方法。该方法不仅考虑了故障观测器和容错控制器之间存在的耦合，而且利用D-稳定引理与H∞控制对增广系统进行设计，在多性能约束条件下实现集成故障估计与容错控制。对于得到的非线性不等式，利用引理2和引理3将其化简为易于求解的线性矩阵不等式，得到了故障观测器与容错控制器存在的充分条件。飞行控制系统的集成故障估计与容错控制仿真结果表明：

（1）本文所提的方法可以对不同的故障进行很好的估计；

（2）相比于分离设计，本文得到的故障估计快速性和准确性更好；

（3）本文提出的集成设计方法的系统输出要优于文献[12]提出的分离设计的系统输出，误差更小。

因此，本文提出的集成设计方法具有较好的理论意义与实际应用价值。