基于最小二乘的全局信息融合方法在分布式POS中的应用
莫明岗,孙兆伟,邹思远
(1.哈尔滨工业大学航天学院,黑龙江哈尔滨 150001;2.北京自动化控制设备研究所,北京 10074)
机载多任务航空遥感系统,是目前空基对地观测的重要发展方向。机载多任务航空遥感系统要实现超高分辨率成像,需获取各载荷的高精度运动参数,进行运动补偿[1]。位置姿态测量系统(Position and Orientation System,POS),可以为成像载荷提供位置姿态运动信息,是目前机载对地观测系统中获取遥感载荷安装点运动参数的主要手段[2,3]。
随着集成多任务成像载荷的新型超高分辨率航空遥感系统的发展,柔性基线多节点运动信息测量有了新的需求,如阵列天线SAR(Synthetic Aperture Radar)性能越高,所需天线数越多,基线越长。受阵风、平台机动等多源扰动影响,柔性长机翼产生多模挠曲变形和颤振耦合运动,部分节点的最大振幅可达米级、挠曲变形角高达10 °左右,柔性基线效应显著。单节点运动信息测量问题,变为柔性基线多节点运动信息和相对空间信息测量的新问题[4,5]。传统单POS已经无法满足不同载荷安置点的高精度运动参数测量需求。因此,为满足各节点间相对位置测量精度需求,多节点柔性基线分布式POS信息融合研究成为制约航空遥感发展的关键技术。
分布式POS 系统,通常是在飞机机腹安装高精度主POS,它是采用高精度IMU(Inertial Measurement Unit)和GPS(Global Positioning System)进行数据融合输出高精度的时空基准信息,为分布在机翼两侧的子IMU提供基准信息,进而通过主子传递对准获得子IMU对应节点处的高精度运动参数[4]。与高精度单POS比较,柔性基线分布式POS由单节点测量变为多节点测量,单个IMU增加为多个IMU,刚性基线变为多级柔性基线。柔性基线效应导致各节点运动信息相互之间动态时变,且状态不确定,现有刚性基线高精度POS信息融合方法无法用于柔性基线多节点时空基准信息精确测量[5]。
通过分布式POS的局部信息融合,即主子传递对准,可以获得柔性基线各节点的局部信息融合值。传统的主子传递对准主要集中在建立近似挠曲变形模型及优化估计方法两方面进行研究。文献[6]基于二阶马尔科夫建立了近似的柔性基线模型,估计挠曲角的随时间的变化,进而实现运动补偿;文献[7]基于非线性UKF(Unscented Kalman Filter)滤波估计,提出自适应后处理估计方法,提高估计精度,实现高精度主子运动信息补偿;文献[8] 基于EKF(Extended Kalman Filter)提出一种双滤波器后处理估计方法,用于提高非线性系统估计精度;文献[9] 基于CDKF(Central Difference Kalman Filter)提出一种双滤波器平滑估计方法,用于分布式POS后处理研究。除此之外还有大量的关于非线性估计方法提高分布式POS传递对准精度的研究。
然而现有传递对准滤波估计的目的是对某一局部节点进行状态估计,得到的结果仅是针对某个节点进行时间维的估计,利用了节点时间维的相关性。而对于整个柔性基线分布式POS系统,机翼形变是连续的,安装在机翼上的遥感载荷在同一时刻它们的运动信息可被认为相互关联,现有主子传递对准方法未对节点空间上运动信息的相关性、连续性进行充分研究。所以为进一步充分利用柔性机翼各子节点运动信息的连续相关性,克服柔性基线效应,有关拟合的方法可以考虑用来解决该问题。
本文在主子传递对准的基础上,利用高精度主POS和各节点子IMU局部状态估计后的所有观测信息,基于最小二乘正交多项式拟合,充分利用各子节点的空间信息相关性,获得系统更高精度、高可靠的全局估计值,提高分布式POS各子IMU的测量效果。最后通过地面模拟实验验证该方法的有效性。
1 机翼柔性基线模型建立
飞机在航行时,机翼的弹性振动分为两种,一是飞机在机动时产生的挠曲变形,二是机翼结构受空气动力作用产生颤振。在飞行过程中,机翼周围会产生高速流体,流体具有粘性及压缩性,使机翼产生变形,变形导致机翼所受气动载荷分布产生变化,载荷分布的变化又会使机翼产生几何变形。气动载荷与机翼变形的相互作用,会引起机翼一定条件下的连续颤振。
柔性机翼会产生多阶模态运动叠加而成的非线性挠曲变形和颤动,其中高阶模态振幅较小,且随机性强,因此柔性基线挠曲运动建模时,主要考虑低阶模态的影响。根据飞机气动特性和结构参数,结合分布式POS布局及柔性基线动力学频谱特性,基于气动弹性动力学理论,采用运动模态叠加方法,建立柔性基线多模态挠曲运动复合模型。
对于大变形机翼弹性变形角,考虑飞机航行时所受载荷,机翼的振动及弹性变形主要是绕机体y轴,即在机翼表面垂直于机翼展向的坐标轴[10],所以在分布式POS信息融合中,本文仅考虑绕y轴的弹性变形角θy。将机翼模拟近似为悬臂梁,其挠曲变形[11]可描述如图1所示。其中,x轴沿机翼展向方向;y轴沿机翼表面垂直于机翼展向的方向;z轴为垂直于机翼表面向上。
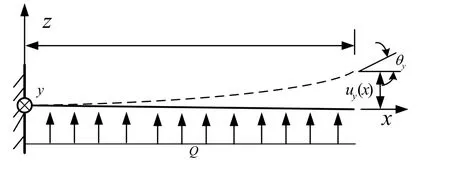
图1 机翼受均布载荷挠曲变形示意图Fig.1 Deformation of the wing under uniform load
基于弹性力学模态叠加理论[11],机翼挠曲运动表示如式(1)所示:
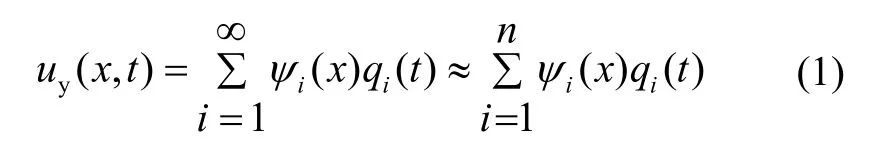
其中,x是机翼展向坐标,uy(x,t)是机翼绕y轴的弯曲变形;n代表杆臂的n阶模态;ψi(x)是第i阶模态的振型函数,qi(t)是第i阶模态的模态坐标。绕y轴的挠曲变形角可表示为:
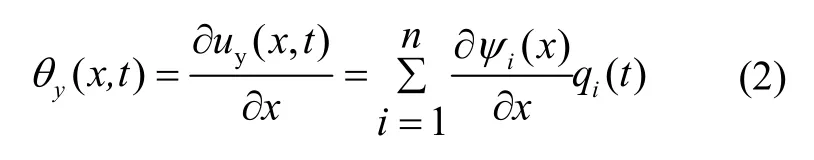
可用模态坐标分析机翼颤振[10],描述为:
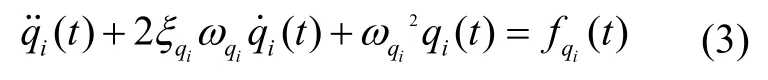
其中,ζqi是模态阻尼系数;ωqi是模态频率;fqi是广义外力。机翼结构受空气扰动产生的广义外力fqi,一般可基于扰动信号的频率范围来确定,大气扰动的频率一般在十几~几十赫兹左右[1]。机翼随时间的振动可以看作机翼受外力产生颤振,由于飞机在正常飞行过程中,模态阻尼系数均为小阻尼震颤ζqi< 1,所以模态坐标函数可视为欠阻尼二阶系统。飞机在巡航过程中,载荷近似为均布载荷,广义外力表示为fqi,可近似为一种阶跃激励,得模态坐标函数为:
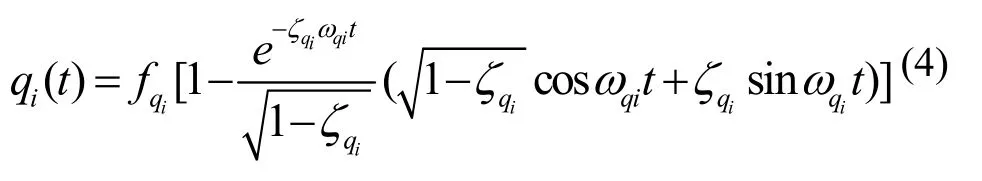
机翼i阶模态对应振型函数表示如下[12]:
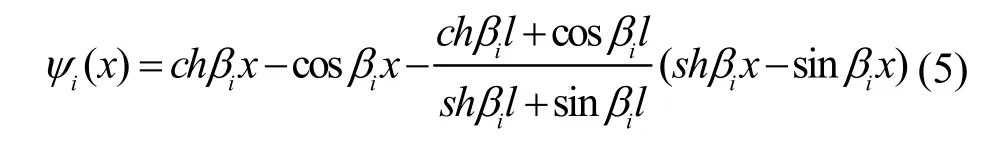
其中,l为单侧机翼总长,βi为待定系数,可通过ANASYS分析及振型曲线拟合得到。
飞机在航行中,受到的大气湍流等外部扰动的频率与一阶模态频率近似,远小于震颤频率,本文取一阶弯曲模态建立机翼挠曲模型错误!未找到引用源。。由于航行器在巡航时,机翼可近似为悬臂梁,机翼所受升力可视为均布载荷,用Q表示。振型函数方程可表示为:
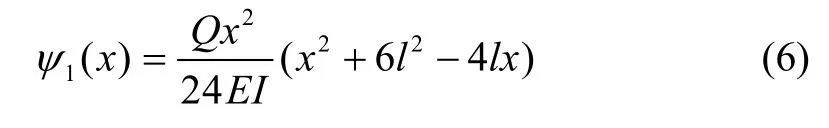
其中,EI为机翼抗弯刚度。
则绕y轴变化取其微分形式为:
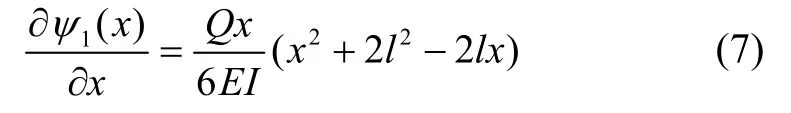
将式(4)(7)代入式(2),挠曲变形角近似表示为:
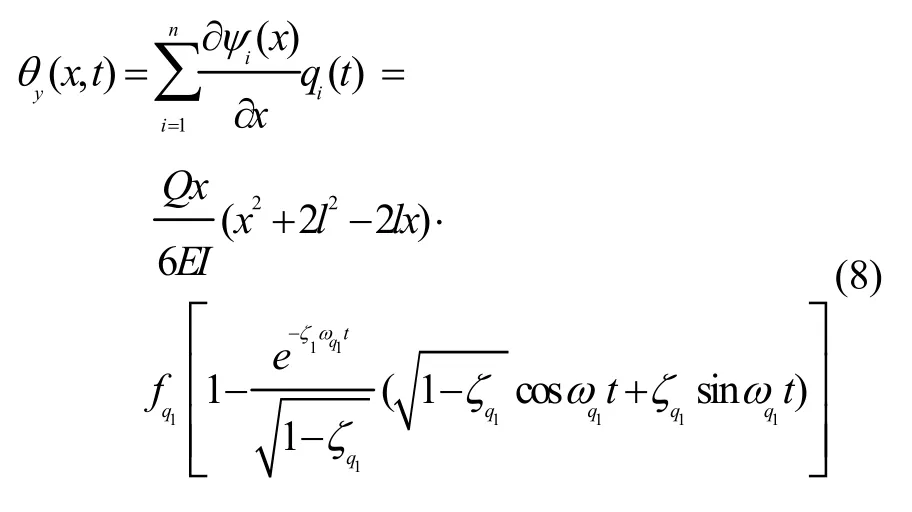
2 基于最小二乘正交多项式全局信息融合算法
针对上述建立的机载柔性基线弯曲变形角模型,可以看出,挠曲变形角是关于时间和空间的二元函数,由时间维的颤振和空间维的弯曲组成。分布式POS通过主子传递对准,各子节点可以充分利用时间上的相关性,分别获得每个子IMU对应节点的随时间变化的运动参数。但通过主子传递对准,只能获得离散的子节点的运动信息,且并未充分利用柔性机翼各子节点的连续空间相关性。为了进一步提高精度,获得连续的节点运动信息,采用基于最小二乘的正交多项式拟合算法进行分布式POS全局信息融合,提高各节点的位置速度姿态测量精度。
设经主子传递对准后各子IMU相对运动参数为 离散序列{f(x,t)}m×p,其中x表示子节点沿机翼展向 的空间坐标,t表示时间,m表示节点个数,p表示采样总时间。根据机载柔性基线各节点变形相关性,f(x,t)间接体现了挠曲角的变形规律,全局信息融合方法主要解决柔性基线多阶模态运动叠加导致的挠曲角的不确定性,为提高各节点的测量精度,融合方法就要无限逼近实际挠曲角变形所带来的载荷运动规律。
正交多项式拟合是基于最小二乘拟合原理的一种函数逼近方法。不要求拟合函数y=g(x)经过所有点(xi,f(xi,tj)),而只需要在给定点xi上残差δi=g(xi)-yi按照某种标准达到最小,通常以欧式范数为衡量标准,即最小二乘拟合,其中,i表示杆臂上第i个子节点,j表示第j时刻。针对所有时刻的分布式 POS 所有节点运动信息,进行正交多项式拟合。根据给定节点x0,x1,…,xm及权函数ρ(x)> 0,推导多项式{Qn(x)},其中n≤m,用递推公式表示Qk(x),即:
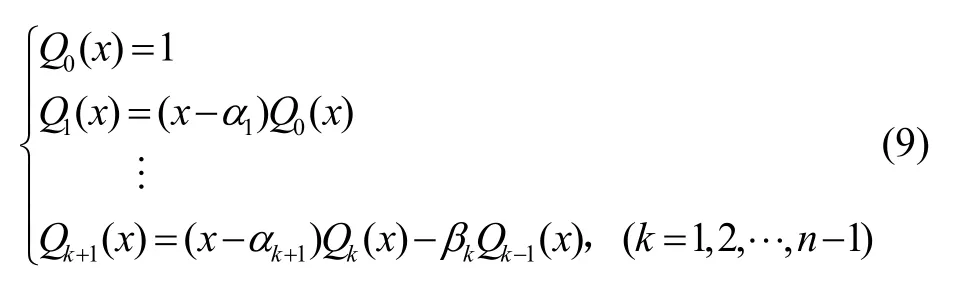
其中,Qk(x)是首项为1的k次多项式,
根据Qk(x)的正交性,有:
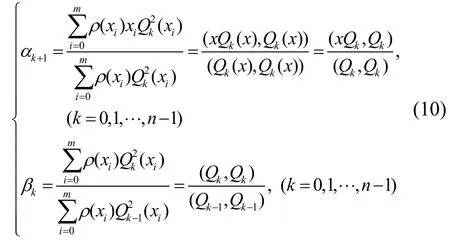
其中,权函数ρ(xi)根据子节点与主POS距离确定,距离越远,柔性基线效应影响越显著,权值越小。根据距离进行归一化,最终确定权值大小。
根据式(9)(10)逐步求得Qk(x),其相对应系数可表示如下:
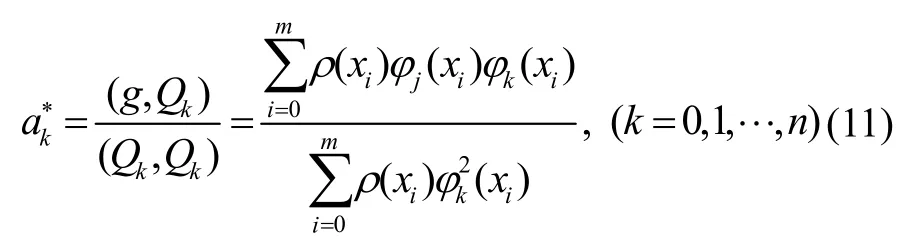
逐步把a*k·Qk(x)累加到S(x)中,最后可求得拟合函数为[13]:

本文将分布式POS各个子系统定义为相应节点x0,x1,…,xm,对每个节点对应的基线值及姿态角进行正交多项式拟合,充分利用各个子节点的信息连续相关性,得到更高精度的基线及姿态角。
3 仿真实验验证
分布式POS多个子IMU传递对准后进行多源信息融合,为充分利用各子POS的时间空间相关性,进行多源全局信息融合,进一步提高分布式POS的测量精度,本节拟基于上述模型及融合方法,开展分布式POS全局信息融合地面模拟实验。
实验技术方案如下:将高精度激光主IMU固定安装在“机身”处。沿机翼模型展向安装低精度子IMU。首先进行分布式POS主子传递对准,再将主子传递对准结果进行全局信息融合。对所有子IMU对应节点的基线结果进行最优拟合,从拟合结果中提取拟合后各子IMU的运动参数。最后对拟合结果进行误差分析。
(1)试验条件
①分布式模拟实验平台:柔性机翼模型、大理石平台、转台。如图2所示。
②POS系统方面:一套高精度激光POS系统;一套较低精度的光纤POS系统,记为2#光纤POS;三个MEMS,分别记为1#MEMS、2#MEMS、3#MEMS;一套高精度光纤IMU,及其配套PCS用于存储IMU数据,以高精度1#光纤POS的处理结果作为基准。其中,陀螺及加速度计精度参数如表1所示。各设备水平距离示意图如图3所示。

表1 陀螺及加速度计精度参数Tab.1 The parameter of the gyroscope and accelerator

图2 分布式模拟实验平台Fig.2 Simulation experiment platform of distributed POS
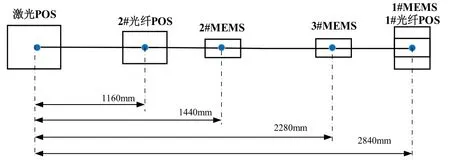
图3 模拟机翼设备安装示意图Fig.3 Schematic diagram of wing equipment installation
(2)实验步骤
①在模拟机翼机身处,安装激光IMU,静止安装于转台,可以降低抖振影响;在第二节点处安装2#光纤 IMU;MEMS精度较低,体积小,作为子传感器分布在机翼各节点,在第三节点处安装2#MEMS IMU,第四节点处安装3#MEMS IMU,1#MEMS IMU与1#光纤IMU固连安装于第五子节点处。其中1#光纤IMU作为基准。1#MEMS IMU与光纤IMU提前做好标定实验,已知测量系统的安装误差角。
②所有传感器安装完毕后,模拟机翼空载条件下静止,然后将机翼末端用固定支架支撑,使机翼达到平直状态。保持静止5分钟。
③将支撑支架撤走,使模拟机翼放置为自然垂下状态,静止5分钟,并记录千分尺数据。然后分别在机翼末端分别放置1 kg、2 kg、3 kg、5 kg砝码,各静止5分钟后记录千分尺数据。
④最后取走砝码,待模拟机翼在空载条件下静止,手动加载两次瞬时脉冲外力,使之自然震颤至静止。
⑤试验结束,关闭实验设备。实验时间约1 h。(3)试验处理及结果
首先,激光IMU作为主POS,激光IMU与差分GPS进行组合导航,获得主POS的位置速度姿态数据,分别对各子IMU进行主子传递对准。将子IMU的运动信息与主POS的运动信息矢量相减,求得对应节点基线距离及横滚姿态信息。本文主要考虑机翼绕y轴的变形。
其次,主子传递对准后,分布式POS系统基于提出的融合方法进行全局信息融合,对多个子POS信息进行空间维正交多项式拟合。由于机载干涉SAR主要需要基线测量信息进行相位补偿,且绕y轴的挠曲变化直接影响基线及横滚角测量精度,又因为在地面演示试验及飞机飞行过程中,我们主要考虑机翼沿杆臂z轴的变形,即垂直于杆臂水平面的方向,所以本文分布式POS测量系统主要以基线和水平姿态横滚角作为评估对象。
各子IMU对应节点处的基线全局融合结果如图4所示,其中x轴表示时间,y轴是模拟机翼的水平坐标,z轴是分布式POS基线测量结果随时间及杆臂水平坐标的变化。
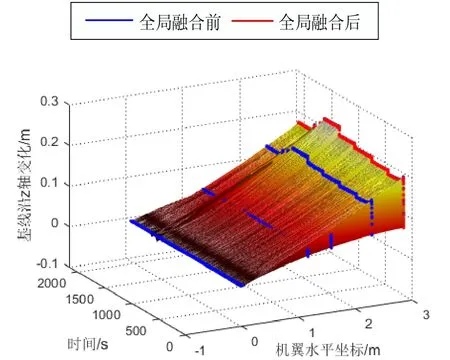
图4 分布式POS各节点基线全局融合时空结果图Fig.4 The results of baseline global fusion in each node of distributed POS
取拟合后某一节点处的基线结果进行验证。以1#光纤IMU传递对准后的的结果作为基准,评估MEMS1节点处(模拟机翼末端,由于杆臂影响,传递对准精度较低)拟合后结果,验证时空拟合精度。MEMS1节点处基线误差结果如图5所示。基线误差统计结果见表2。
根据实验步骤,每次加入外部激励不同,从自然垂放段进行统计分析。整个实验分成八个阶段,其中6、7段为动态振荡,其他段为不同加载的准静态情况。根据统计结果可以看出,经过全局信息融合后,1#MEMS节点处的基线测量精度在x轴、y轴和z轴均有所提高。分别平均提高了1.893 mm、0.461 mm和2.183 mm。
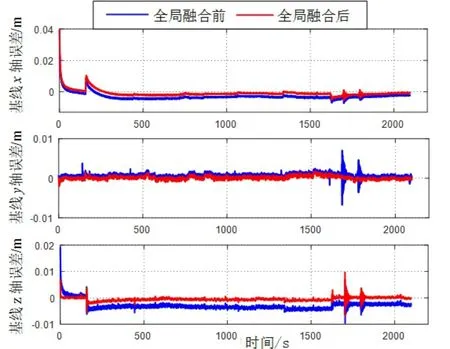
图5 MEMS1处节点基线误差结果对比图Fig.5 Comparison of baseline error results of the node at MEMS1
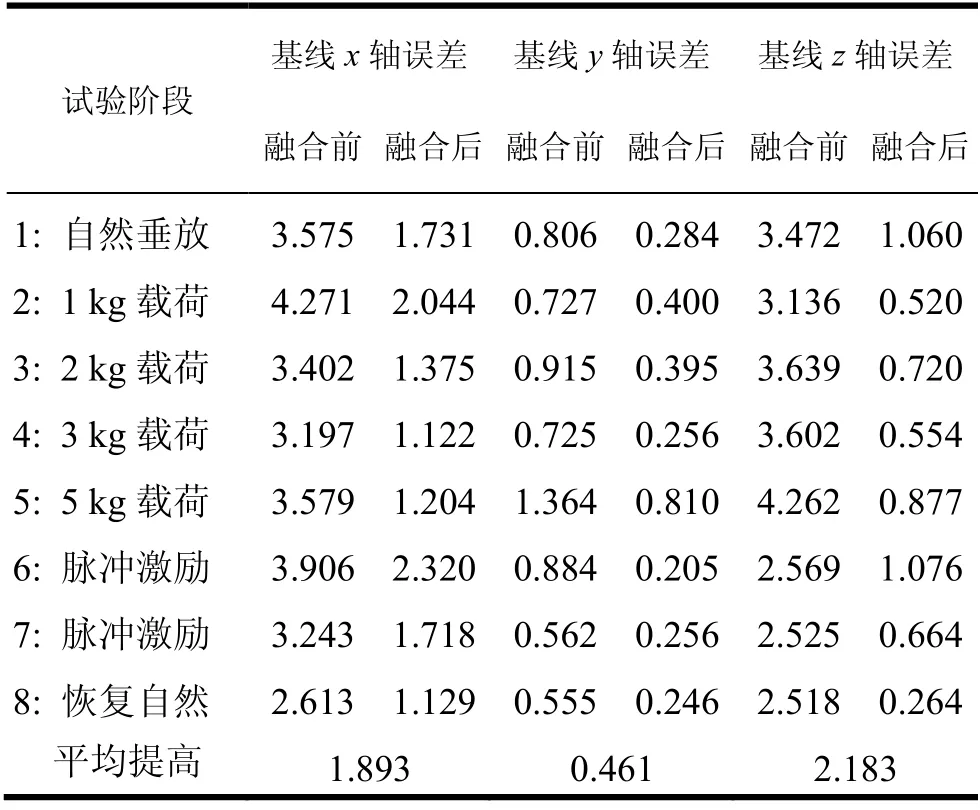
表2 MEMS1节点处基线误差统计结果表RMS(10-3m)Tab.2 The results of the baseline error of the node at MEMS1
处理各子IMU对应节点处的横滚角的全局融合结果如图6所示。以1#光纤IMU传递对准后的的结果作为基准,对MEMS1节点处的横滚角误差进行分析,融合前后误差结果如图7所示。MEMS1节点处横滚角误差统计结果如表3所示。
根据统计结果可以看出,经过全局信息融合后,1#MEMS节点处的横滚角测量精度均有所提高。在支撑阶段,模拟机翼弯曲变形小,对角度影响较小,精度提高不明显。统计模拟机翼有明显变形阶段的RMS值,横滚角平均精度提高了0.023°。综合整个实验结果,可以看出该全局信息融合方法,在主子传递对准的基础上,能够充分利用所有子节点的运动信息连续相关性,有效提高分布式POS的测量估计精度。
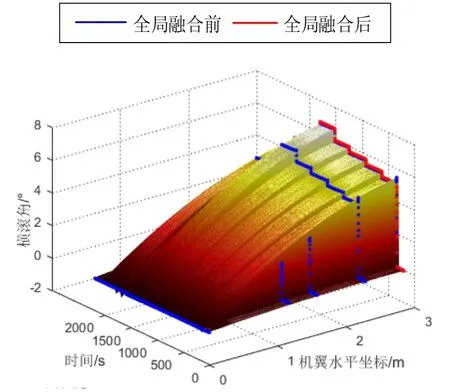
图6 分布式POS各节点横滚角全局融合时空结果图Fig 6.Global fusion results of roll at each node in distributed POS
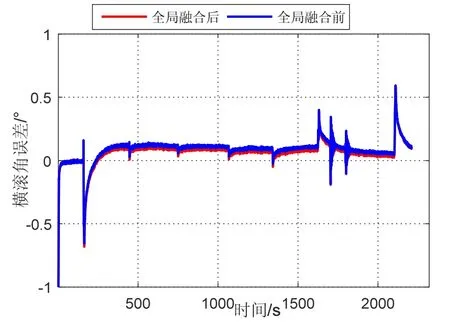
图7 MEMS1处节点横滚角误差结果对比图Fig 7.The comparison of the results of roll erro of the node at MEMS1
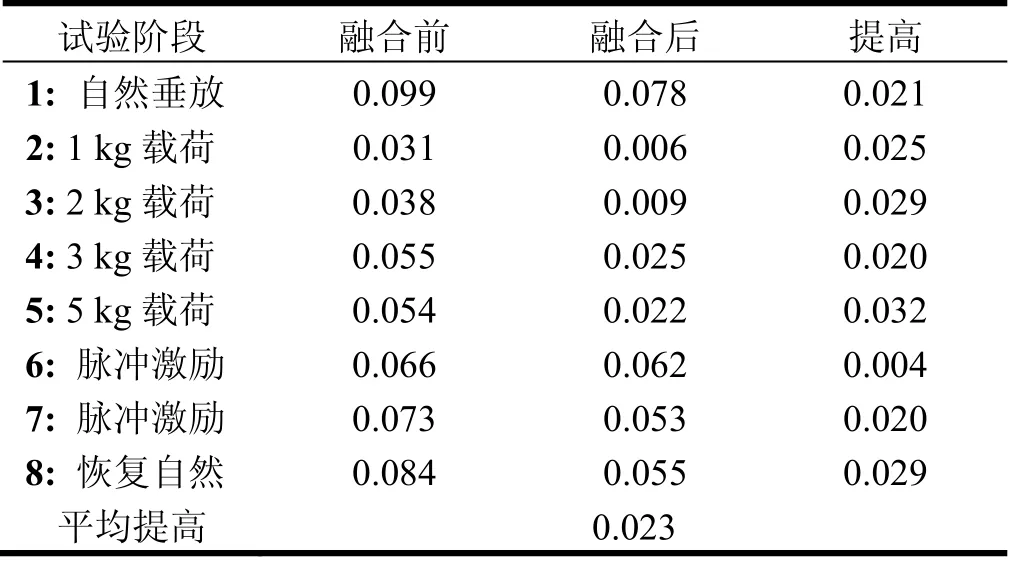
表3 MEMS1节点处横滚角误差统计结果表RMS(°)Tab.3 The results of the roll error of the node at MEMS1
4 结 论
本文提出的基于最小二乘的全局信息融合方法,充分利用各子节点的信息相关性,获得系统更高精度、高可靠的全局融合值,应用于分布式POS传递对准后处理,可有效提高子IMU测量精度。地面仿真验证,x轴、y轴、z轴基线精度平均提高了1.893 mm、0.461 mm和2.183 mm,水平姿态横滚角精度平均提高0.023 °,提升了分布式POS测量性能。

