一种用于重力梯度动态测量的载体环境引力梯度补偿方法

严 飞，李 达，李 中,3，孟兆海,3,4,5，王怀君

（1.海装北京局驻天津地区某军事代表室，天津 300131;2.天津航海仪器研究所，天津 300131;3.中船集团航海保障技术实验室，天津 300131;4 中国科学院地质与地球物理研究所，北京 100029;5 中国科学院油气资源研究重点实验室，北京 100029）

重力梯度是重力矢量的空间变化率，重力梯度仪是用于测量重力梯度的精密设备，基于Bell Aerospace公司提出的旋转加速度计测量原理的重力梯度仪是迄今唯一实用的近地表动态重力梯度仪[1-3]。重力梯度仪的核心部件是重力梯度敏感器，动态测量时，重力梯度敏感器安装在惯性稳定平台上，稳定在地理坐标系下，测量地理坐标系下的重力梯度。在测量过程中，飞机、舰船等载体的姿态变化，将引起载体质量分布与重力梯度敏感器的相对位置发生变化。载体质量对重力梯度敏感器产生的引力梯度将随着载体姿态变化而产生变化，形成载体环境引力梯度变化[4,5]。随着重力梯度仪精度水平不断提高，在动态测量中载体环境引力梯度变化已成为高精度重力梯度仪的一项重要误差来源[6]。

本文基于重力梯度张量在不同坐标系下的转换关系建立了载体环境引力梯度变化的解析模型，以此为基础建立了回归方程。通过Tikhonov正则化方法抑制了该方程解的不适定问题，得到载体环境引力梯度在载体坐标系下的数值解，以此进行载体环境引力梯度变化改正，通过实测海试数据验证该方法的有效性，为动态重力梯度仪研制提供参考。

1 载体环境引力梯度变化模型

1.1 重力梯度仪测量原理

重力梯度是重力位的空间二阶导数，表征重力矢量的空间变化率。在地理坐标系中，重力矢量可以分解为x，y，z三个方向上的三个分量中，每一分量沿平行于坐标轴方向均有一个梯度。因此，重力梯度张量共有9个分量,可将其表示为：

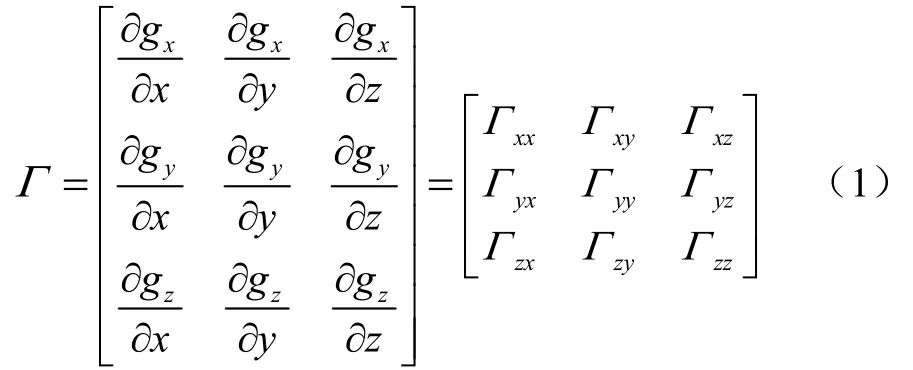
式中，Γij（i,j=x,y,z）为梯度张量的分量，表示重力分量gi在j方向上的变化率。

旋转加速度计式重力梯度仪主要由重力梯度敏感器和惯性稳定平台两个关键组件构成。重力梯度敏感器主要用于完成重力梯度张量水平分量的测量；惯性稳定平台则用于承载重力梯度敏感器，为重力梯度动态测量提供稳定的动力学环境。如图1所示，重力梯度敏感器基于加速度计位置差分的测量原理，通过机械旋转的方式将旋转中心处的重力梯度张量水平分量调制到系统旋转频率的二倍频处，加速度计四路和信号与重力梯度张量水平分量之间的关系可表示为[7]：

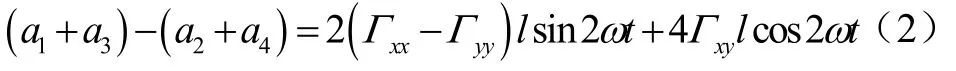
式中，a1、a2、a3、a4是四只加速度计敏感轴方向的加速度，l是加速度计检测质心到旋转中心的距离，Γxx、Γyy、Γxy是测量平面内对应方向的重力梯度张量分量，单位是 E（1 E=10-9s-2），ω是旋转圆盘的旋转角速率。进行动态测量时，惯性稳定平台采用三环固定指北半解析式控制方案，在隔离载体角运动的同时，将重力梯度敏感器稳定在地理坐标系，为测量提供坐标基准。

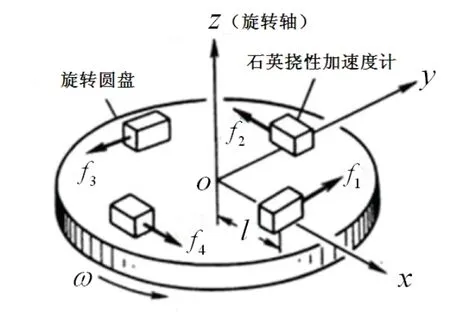
图1 重力梯度敏感器测量原理示意图Fig.1 Schematic diagram of measuring principle of gravity gradient sensor

1.2 重力梯度坐标变换

依据重力势函数梯度和方向导数关系，得到重力梯度张量在不同坐标系下的变换公式为[8]：

式中：Γn是重力梯度张量在地理坐标系下的投影；Γb是重力梯度张量在载体坐标系下的投影；Cbn是从载体坐标系到地理坐标系的坐标变换矩阵。定义地理坐标系为“东-北-天”地理坐标系时，依据欧拉转动原理，Cbn可表示为：

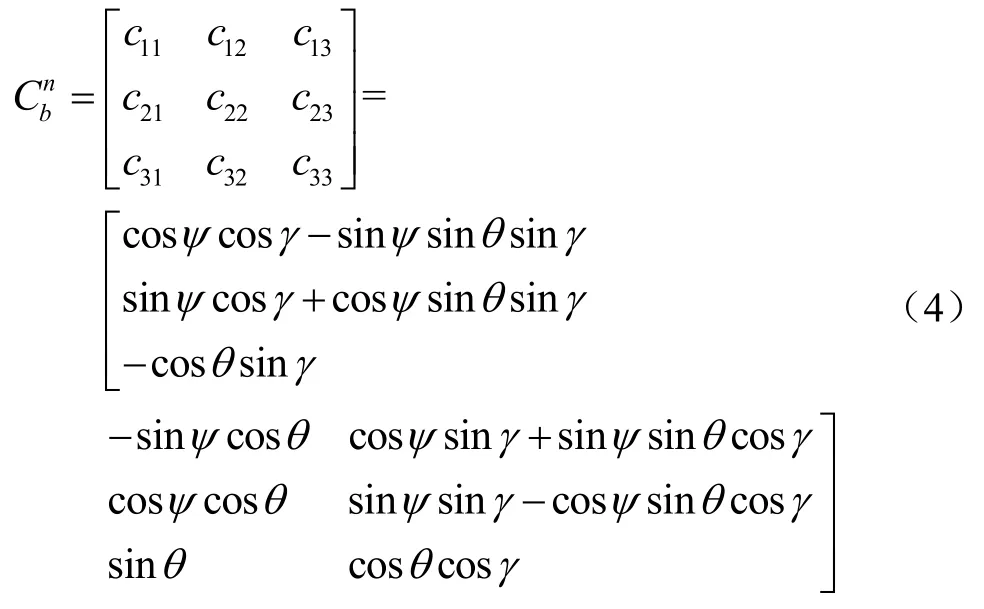
式中，ψ、θ和γ分别为载体的航向角、俯仰角和横滚角。

重力场是一个保守场，表明重力场是一个无源场，且场线在空间内不闭合，有[9]：

式（5）表示重力场的旋度为零，说明重力梯度张量矩阵具有对称性，即：

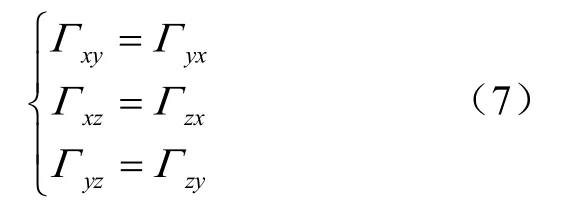
式（6）表示重力场的散度为零，意味着重力梯度张量矩阵的迹为零，即：

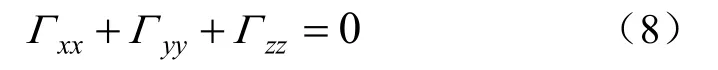
因此，得到重力梯度的坐标变换公式为：

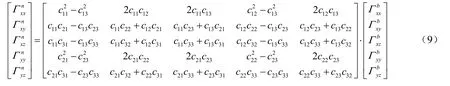
1.3 载体环境引力梯度变化模型

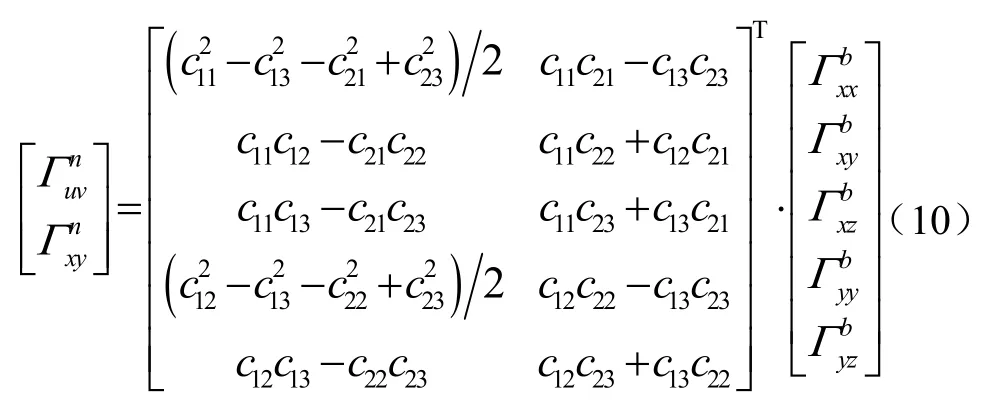
式（10）可简写为：

式中，Rbn为从载体坐标系到地理坐标系的重力梯度张量列向量的坐标变换矩阵。

在动态测量过程中重力梯度敏感器始终稳定在地理坐标系，载体质量的分布与敏感器的相对位置发生变化，形成载体环境引力梯度变化。结合式（11），得到重力梯度仪载体环境引力梯度变化的解析方程为：

式中，δTen是由载体环境引力梯度变化引起的水平分量重力梯度测量误差；Teb是载体质量在载体坐标系下对重力梯度敏感器旋转中心位置产生的引力梯度。

利用实测舰船姿态信息结合舰船结构引力梯度正演计算，满载排水量为5000 t的舰船在测线上载体环境引力梯度变化量约为30 E量级。

2 基于Tikhonov正则化的载体环境梯度误差补偿方法

2.1 回归方程

依据式（12），可以写出考虑载体环境引力梯度变化的重力梯度仪测量方程为：

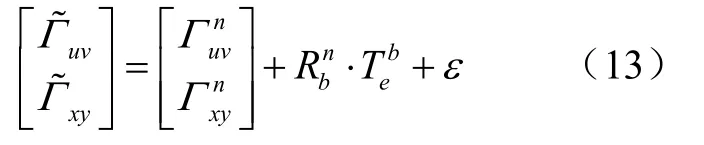
利用载体环境引力梯度变化和载体姿态的解析关系建立回归方程，可用多元回归的方式求取载体质量在载体坐标系下对重力梯度敏感器旋转中心位置引起的引力梯度变化，从而结合载体姿态信息对测量数据进行载体环境引力梯度变化改正，提高测量精度。

2.2 解的不适定分析

利用最小二乘法求解式（14），可得[11]：

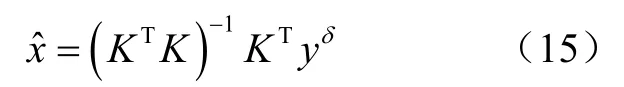
式中是x的估计解，即载体质量在载体坐标系下对重力梯度敏感器旋转中心位置引起引力梯度的估计值。

在不考虑回归算子K的扰动时，有估计解的扰动式为[12]：

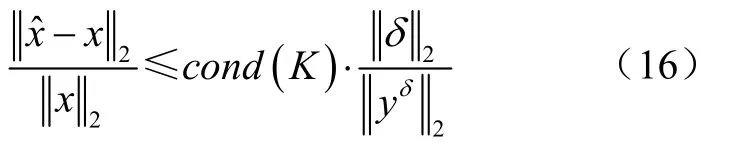
式中cond（K）是算子K在2范数意义下的条件数，其计算式为：

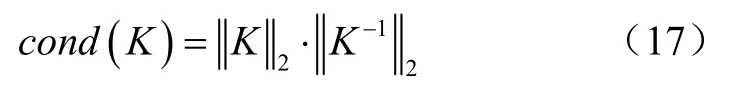
式（16）表明了回归方程式（14）中的非线性量δ以cond（K）的倍数进行放大，因此为抑制扰动量δ对估计解的扰动，要求算子K的条件数越小越好。

在进行重力梯度测量作业时，通常由飞机或舰船搭载重力梯度仪，在固定区域内沿网格化测线测量。在测线中保持匀速直线运动，最大程度降低载体加速度对于重力梯度测量的干扰。因此在测量过程中载体俯仰角和横滚角的波动较小，只有航向角能产生较大变化。而在飞机爬升和舰船转弯等俯仰角、横滚角波动较大的航行状态下，载体运动加速度干扰同样很大，此时重力梯度仪无法实现高精度测量。

某次重力梯度仪船载试验中两条反向的测线船体俯仰角、横滚角和航向角如图2，3所示（定义为测线1#和测线2#），两条测线的航迹线如图4所示。从中可以看出测量过程中船体俯仰角波动峰峰值为2°，横滚角波动峰峰值为2°，航向角波动峰峰值为5°。计算cond（K）的结果如表1所示。

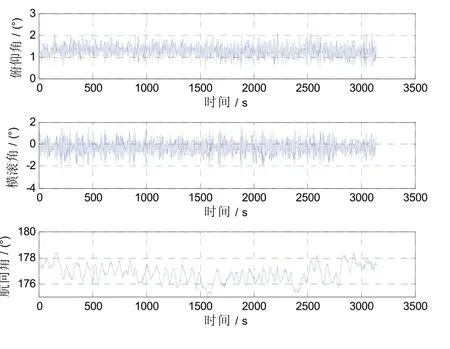
图2 重力梯度仪船载试验中测线1#船体航姿曲线Fig.2 Line 1# ship attitude curve in the shipboard test of gravity gradiometer

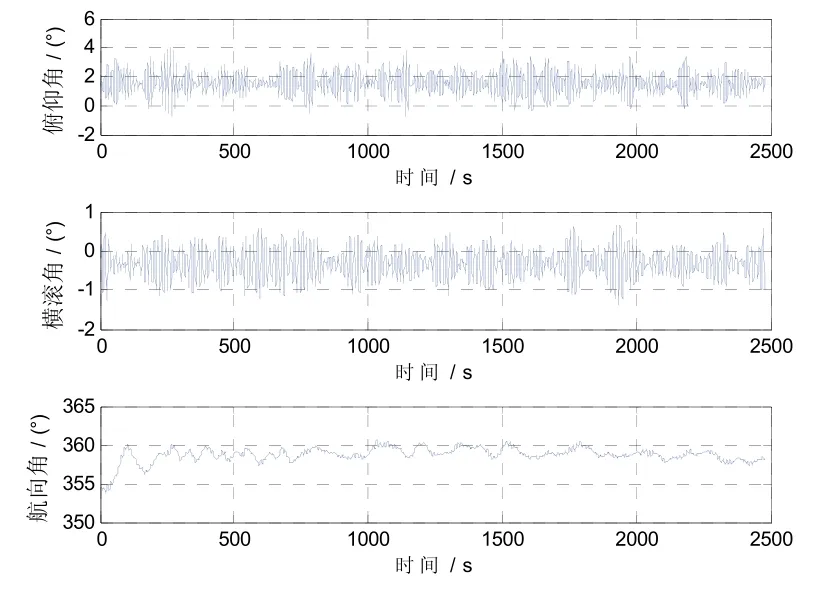
图3 重力梯度仪船载试验中测线2#船体航姿曲线Fig.3 Line 2# ship attitude curve in the shipboard test of gravity gradiometer

图4 重力梯度仪船载试验中测线1#和测线2#航迹线Fig.4 The track lines of line 1# and line 2# in the shipborne test of gravity gradiometer

表1 测线1#和测线2#的cond(K)计算结果Tab.1 Calculation results of cond(K)of line 1# and line 2# respectively

从表1中可以看出，利用两条反向的测线1#和2#上的船体姿态数据，cond（K）为3×103～5×103量级，仍是病态的，即具有严重的复共线性特性。因此考虑利用两条正交的测线进行回归分析，降低cond（K）的数值。

引入一条与测线1#正交的测线，定义为测线3#，其船体俯仰角、横滚角和航向角如图5所示，测线1#和测线3#的航迹线如图6所示，利用1#、2#和3#测线的数据计算cond(K)的结果如表2所示。

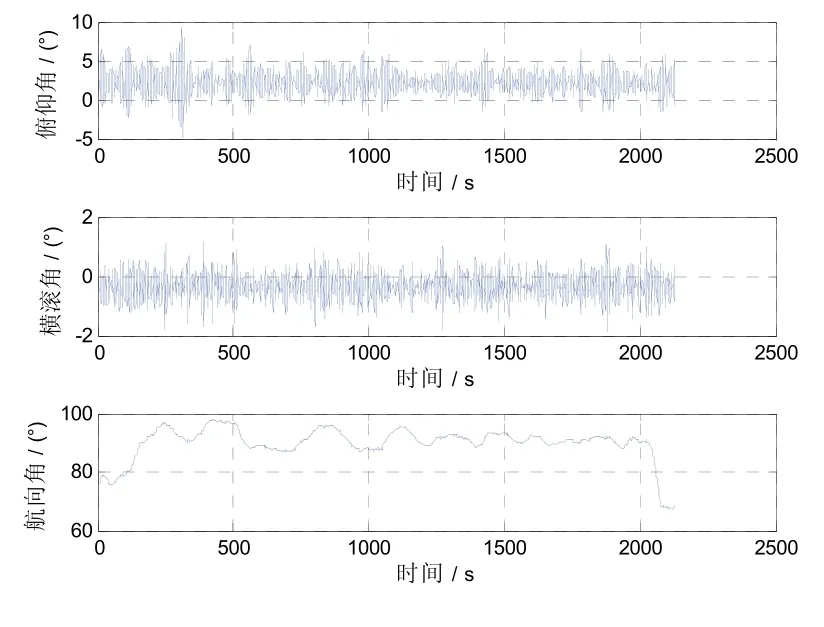
图5 重力梯度仪船载试验中测线3#船体航姿曲线Fig.5 Line 3# ship attitude curve in the shipboard test of gravity gradiometer

图6 重力梯度仪船载试验中测线1#和测线3#航迹线Fig.6 The track lines of line 1# and line 3# in the shipborne test of gravity gradiometer

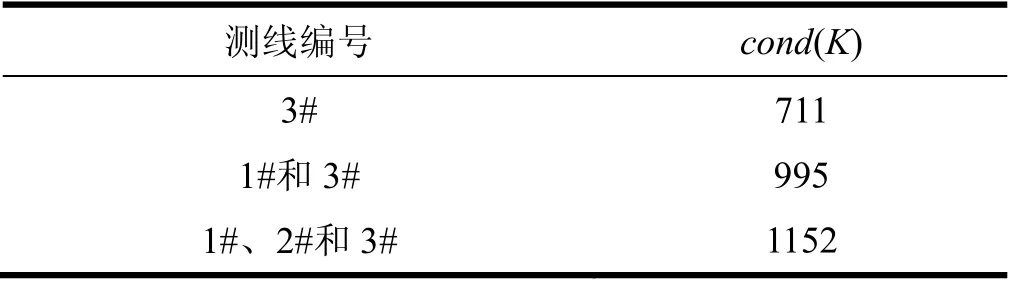
表2 测线1#和测线3#的cond(K)计算结果Tab.2 Calculation results of cond(K)of line 1# and line 3# respectively

从表2中可以看出，即使利用3条正交的测线（1#、2#和3#）上的船体姿态数据计算cond（K），数值仍在1×103量级，仍是病态的，在式（14）中会放大测量信号yδ中的扰动量δ。同时，回归方程的扰动量δ不仅包含测量噪声，还包含真实的地表重力梯度信号，回归方程的扰动量是拟合量的5倍以上，为防止“过拟合”的情况，必须选择合理的正则化方法，以求取回归方程的精确估计解。

2.3 基于Tikhonov正则化的回归方法

目前解决最小二乘回归病态问题应用较广的方法是Tikhonov正则化方法[13]，它通过求解如式（18）所示的最小化问题获得正则数值解。

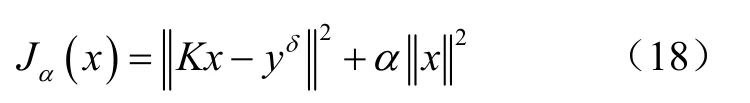
可通过式（19）得到。

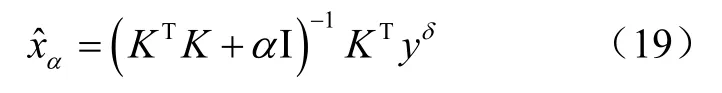
式中，I是单位矩阵，α是控制参数（α＞ 0）。其中（KTK+αI ）-1KT是正则化算子。Tikhonov正则化方法的基本思想是牺牲估计解的无偏性将系数矩阵K的病态问题转化为良性问题，使得正则数值解更加逼近于精确解x。

2.4 正则化参数确定

目前已有大量文献研究了Tikhonov正则化方法中正则化算子的构造和相关正则化参数的选取[14,15]，本文采用半物理仿真的方式选择控制参数α的最佳数值。通过引力梯度正演的方法仿真得到该方程的理论解x，利用实测重力梯度数据和实测姿态信息结合式（14）分别计算δ、K和yδ。定义误差比为。控制参数α在［0.0001,100］范围内分别求取回归方程的估计解，计算步长为0.0001，并计算误差比，结果如图7所示。作为对比，再使用常规最小二乘的方法求取估计解，并计算误差比。典型计算结果见表3。

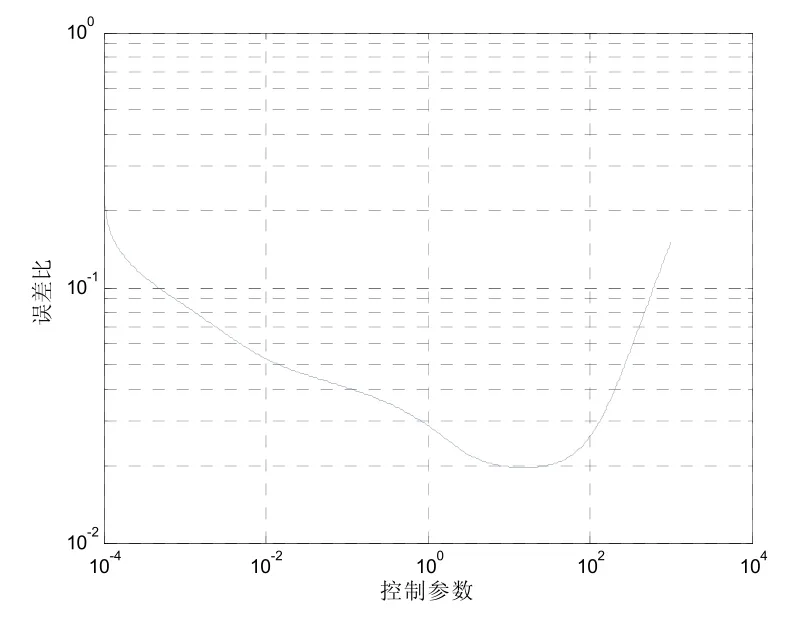
图7 不同控制参数α时的误差比Fig.7 Error ratio of different control parameter α

表3 不同条件下回归方程估计解的计算结果Tab.3 Calculation results of estimated solution of regression equation under different conditions

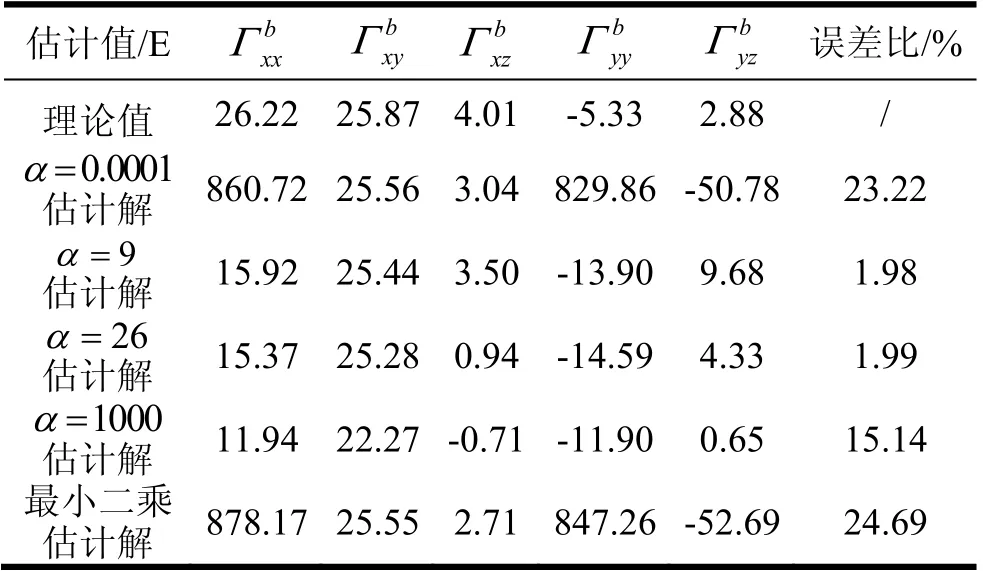
表3 不同条件下回归方程估计解的计算结果Tab.3 Calculation results of estimated solution of regression equation under different conditions

估计值/E b Γ b xx Γ b xy Γ b xz Γ b yy Γ 误差比/%yz理论值 26.2225.874.01 -5.332.88 / α估=计解 860.7225.563.04829.86 -50.7823.220.0001估α计=解 15.9225.443.50 -13.909.681.989 α估计=解 15.3725.280.94 -14.594.331.9926 α估=计解 11.9422.27-0.71 -11.900.6515.141000最估小计二解乘 878.1725.552.71847.26 -52.6924.69

结合图7和表3中可知，与较常规最小二乘方法比，Tikhonov正则化的方法只要将控制参数α选取在9～26之间，能将补偿量的误差比从24.69%降低至2%以内，且相差不大。因此在本研究中选择α= 15。

3 试验验证

3.1 载体环境引力梯度估计

重力梯度仪船载试验中测线1# 和2# 两条重复线的测量数据未进行载体环境引力梯度补偿时，重力梯度测量信号结果如图8和9所示。结合载体姿态数据使用式（19）进行载体环境梯度估计，分别使用常规最小二乘法和Tikhonov正则化方法进行回归估计，计算结果如表4所示。

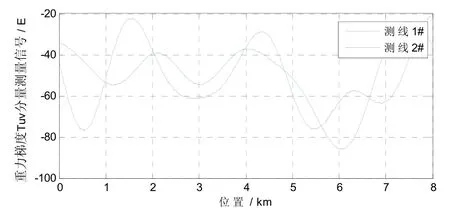
图8 重力梯度 Γuv分量原始输出信号Fig.8 Original output signal of gravity gradient component Γuv

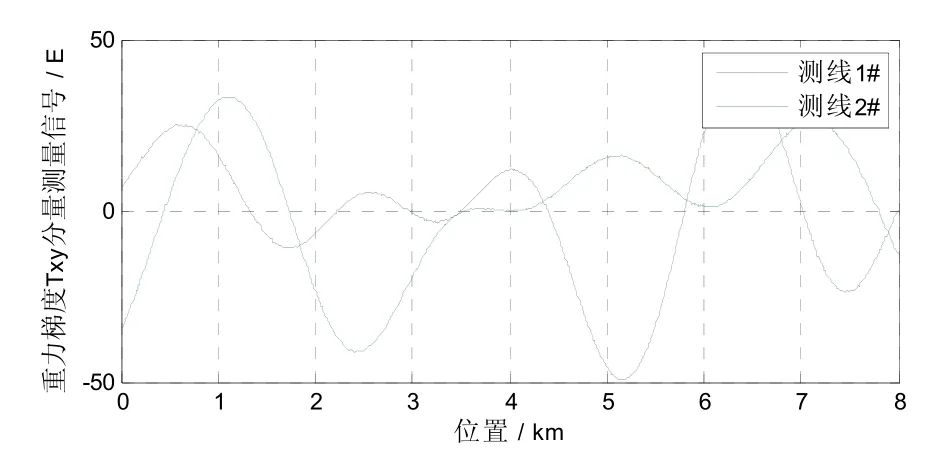
图9 重力梯度 Γxy分量原始输出信号Fig.9 Original output signal of gravity gradient component Γxy

表4 载体环境引力梯度估计结果Tab.4 Calculation results of carrier environmental gradient

3.1 重力梯度测量结果及精度评价

将Tikhonov正则化法和常规最小二乘法得到的载体环境梯度估计值代入式（14），进行重力梯度信号载体环境引力梯度变化补偿，使用Tikhonov正则化法补偿后重力梯度测量信号结果如图10和11所示，使用最小二乘法补偿后重力梯度测量信号结果如图12和13所示，分别计算补偿前后重力梯度信号内符合精度，如表5所示。

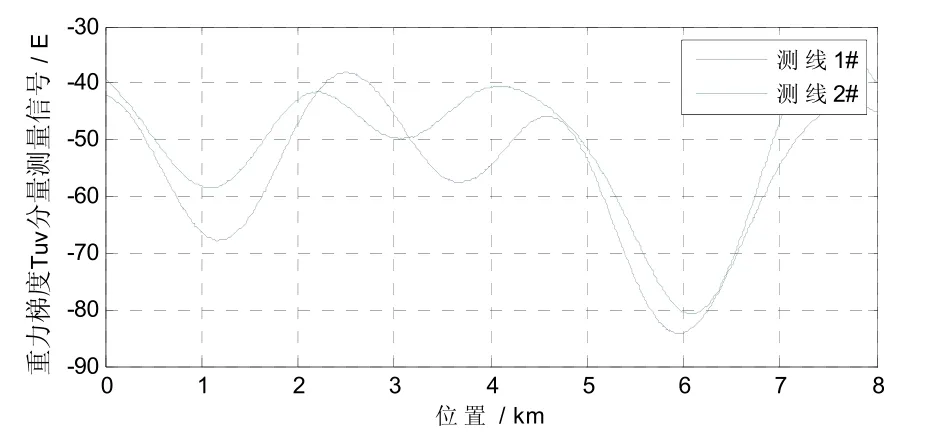
图10 Tikhonov正则化法载体环境引力梯度变化补偿后重力梯度分量信号Fig.10. component signal of gravity gradient after compensation of environmental gravity gradient change by Tikhonov regularization method

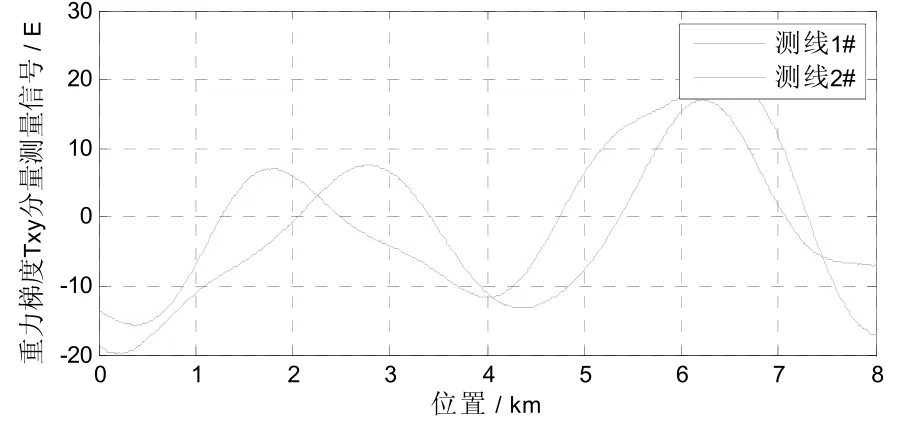
图11 Tikhonov正则化法载体环境引力梯度变化补偿后重力梯度 Γxy分量信号Fig.11 Γxy component signal of gravity gradient after compensation of environmental gravity gradient change by Tikhonov regularization method

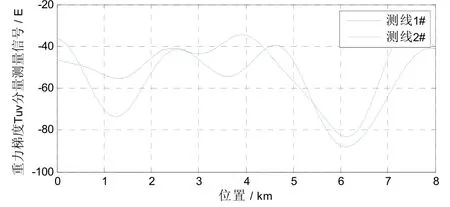
图12 最小二乘法载体环境引力梯度变化补偿后 重力梯度 Γxy分量信号Fig.12 Γuv component signal of gravity gradient after compensation of gravity gradient change of carrier environment by least square method

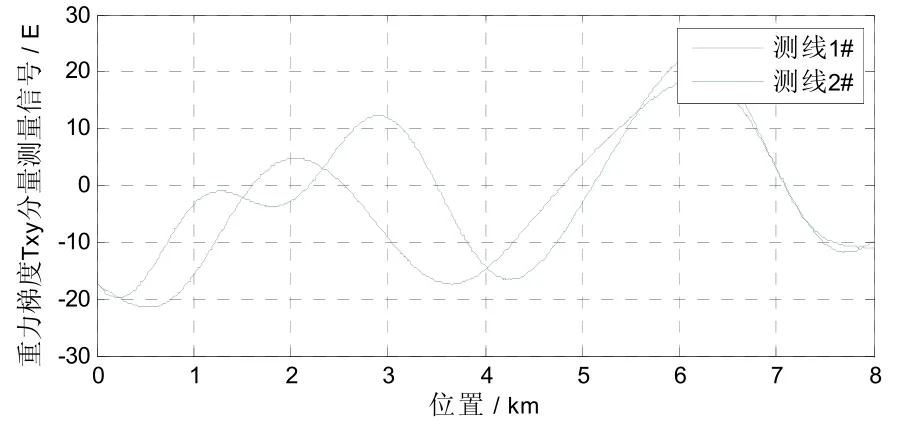
图13 最小二乘法法载体环境引力梯度变化补偿后 重力梯度 Γxy分量信号Fig.13.Γxy component signal of gravity gradient after compensation of gravity gradient change of carrier environment by least square method

表5 载体环境引力梯度变化补偿前后内符合中误差对比Tab.5 Comparison of the mean square error of the internal coincidence before and after compensation for the change of the gravity gradient of the carrier environment

4 结 论

本文针对重力梯度仪动态测量过程中载体环境引力梯度干扰的问题，建立了动态测量过程中载体环境引力梯度变化的传递模型，以此为基础建立了回归方程。通过Tikhonov正则化方法抑制了该方程解的不适定问题，利用半实物仿真的方法得到最优控制参数α的取值范围，使补偿量的误差控制在2%。经实测船载数据验证，该方法切实可行，补偿后内符合中误差较原始重力梯度测量信号中误差分别降低19 E和 21 E，较常规最小二乘法进一步降低7 E和3 E，补偿后重力梯度仪两路测量信号内符合中误差均达到优于10 E的精度水平。