一种车载捷联惯导行进间QUEST优化粗对准算法

韩勇强，王新健，谢 玲，陈家斌

（北京理工大学，北京 100081）

初始对准一直是惯性导航系统极为重要的问题，传统的静基座对准多使用解析式粗对准方法[1]，精度满足使用要求，但对准过程中载体处于静止状态，缺乏机动性。针对这一问题，文献[2-4]基于姿态矩阵分解的思想，将载体姿态分为三个独立的部分，提出了计算初始姿态的关系式，但是未对如何计算姿态角进行有效说明。文献[5,6]在粗对准计算过程中使用双矢量叉乘计算方法，没有充分利用两个积分时间段信息之间的关系，对信噪比较低的地球旋转角速度依赖较高，对重力矢量信息的利用不足。文献[7,8]分别使用卡尔曼滤波与航位推算方法，但简化了粗对准过程，导致航向角收敛速度慢，精度受到限制。目前运动基座粗对准多使用QUEST算法，该算法能够克服上述缺点，具有适中的计算复杂程度。文献[9,10]使用QUEST算法，实现了晃动基座下的粗对准，但其采用批处理方法，并未利用里程计对载体姿态进行实时反馈，不利于嵌入式实现。同时，由于惯导及里程计均存在一定误差，上述文献均未对误差进行预处理，精度较差。

里程计自主性好，信号不易受干扰，标定后与车体坐标系重合，可以更直接地得到车体坐标系下的速度，结合地理坐标系下的重力矢量，可以方便地得到车体与地理坐标系的转换关系。基于以上问题，本文提出了一种基于里程计辅助的QUEST优化算法，并经过实验验证，实现了车载捷联惯导行进间粗对准，减小了系统粗对准误差。

1 坐标系定义

(1)e系为地心坐标系，原点位于地心，z轴沿地球自转方向，x轴位于赤道平面内，从地心指向车体初始位置子午线，x轴、z轴与y轴构成右手坐标系。e系与地球固联。

(2)i系为惯性系，与初始时刻e系指向相同，且不与地球固联。

(3)b系为车体坐标系，x、y、z轴等分别指向车体右、前、上方，且与车体固联。

(4)n系为车体所在位置的当地地理坐标系，x轴指向正东，y轴指向正北，z轴指向天。

2 粗对准算法研究

初始对准其实就是利用里程计和惯导的输出，求解在初始状态下b系与n系的转换关系，即确定姿态矩阵Cbn。然后再将计算得到的姿态、速度、位置，反馈回算法当中，从而实现车载惯导行进间的粗对准。算法原理图如图1所示。

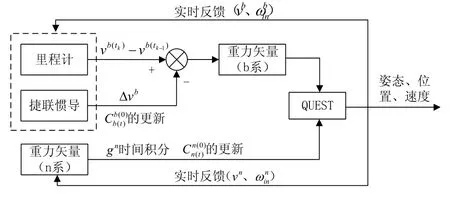
图1 粗对准算法原理图Fig.1 Diagram of the coarse alignment algorithm

2.1 重力矢量信息的计算

基于时间更新过程，我们可以对姿态矩阵进行分解：

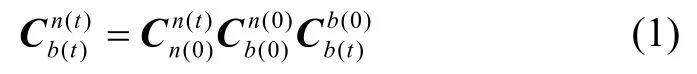
这样姿态矩阵便被分成三部分，导航系的更新，车体坐标系的更新以及初始姿态矩阵。这为我们后续的计算带来方便。

其次,写出n系下捷联惯导的速度比力方程：

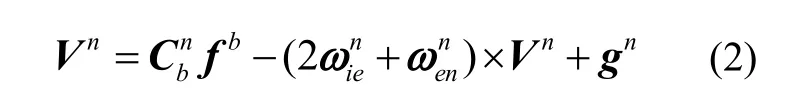
其中，Vn为车体在导航坐标系下的速度，Cbn为t时刻的姿态矩阵，fb为捷联惯导测量到的比力，为n系下的地球自转角速度，为n系下n系相对于e系的角速度，gn为n系下当地的重力矢量。

式（2）经过变换后可以写成

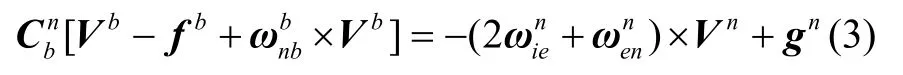
将式(1)代入式(3)并在方程左右两侧同时乘以，于是得到：

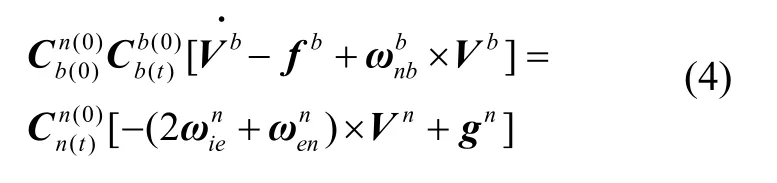
对等号两边同时进行积分

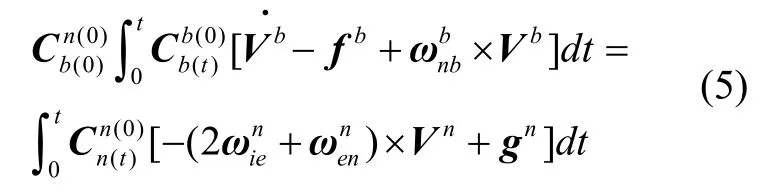
和分别是车体坐标系和导航坐标系的更新，它们可以通过式(6)的方法来进行确定。

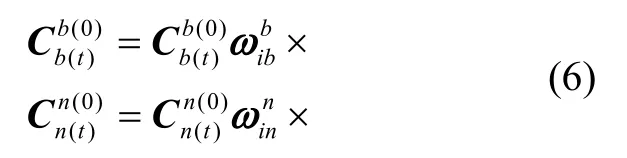
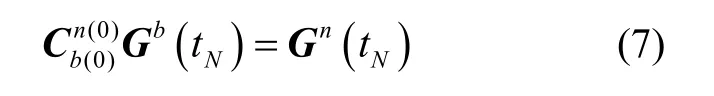
其中，

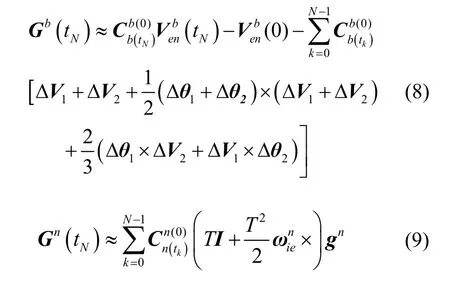
其中，T为采样时间间隔，tk=kT，k=0,1,2,…,N-1；ΔV1、ΔV2与 Δθ1、Δθ2分别为惯导在T时间间隔内分两次采到的速度与角度增量，的值可以通过里程计的输出获得。

2.2 优化的QUEST算法

使用2.1所描述的方法之后，可以得到多个时刻的Gb（tN）与Gn（tN），计算初始姿态矩阵的过程其实就是寻找一个矩阵，使其可以尽量满足式（7）的关系。常用的方法有正交向量计算法和最小二乘法。但经过实验证明，正交向量计算法只利用最终时刻t以及t/2时刻的向量，信息利用不足，难以得到正确的姿态结果，最小二乘法得到的结果为非正交矩阵，需要多次正交化处理，且整个计算过程受随机误差的影响较大，有较大概率出现错误的航向角结果，稳定性较差。本文提出一种基于QUEST的优化算法，利用重力矢量模值误差与实时反馈的方法，实现了更加稳定快速的粗对准过程。

（1）QUEST算法

QUEST算法具有广泛的应用，其中一种便是应用于姿态估计。假设矩阵A为我们要求取的矩阵，可以定义如下的最优估计模型：

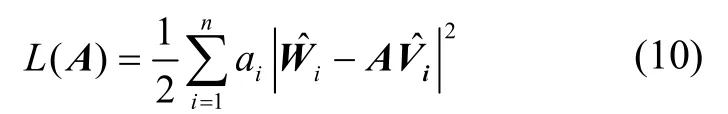
其中，与分别为同一变量在两个不同观测系下得到的值。ai为不同时刻信息的权重，视不同的应用情况而定。那么增益函数g(A)可以定义为

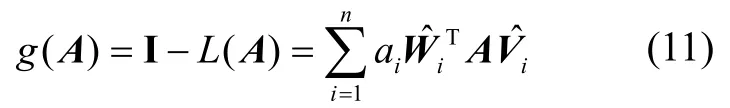
当L(A)达到极小，即g(A)达到极大时，矩阵A即为求得的最优结果。把g(A)写成如式（12）形式。

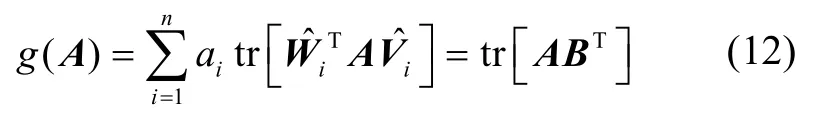
其中，

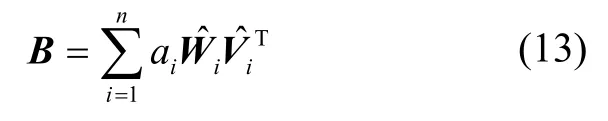
将式（12）改为姿态四元数进行求解，则增益函数可以重新表示为

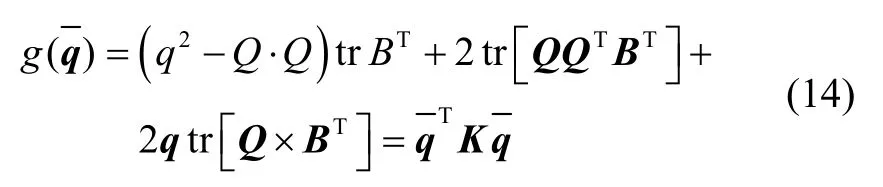
其中，K为4×4矩阵

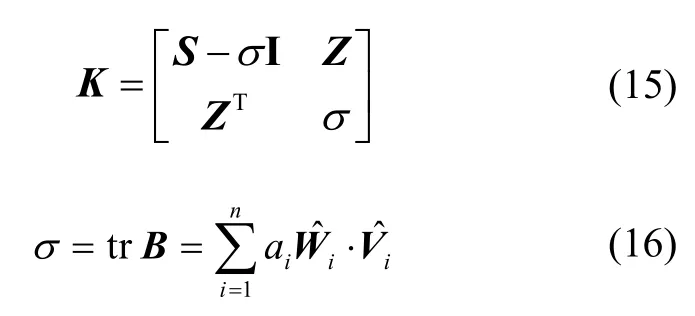
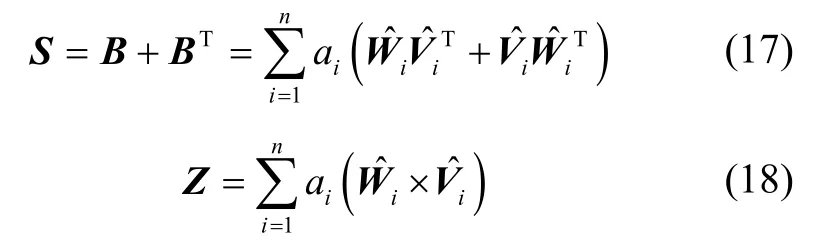
因此，想要取得极值需要满足g'()=0，即是K的特征向量，且λ取得最大时，对应的特征向量即为所求。因此，对于任何一个特征值λ，均有

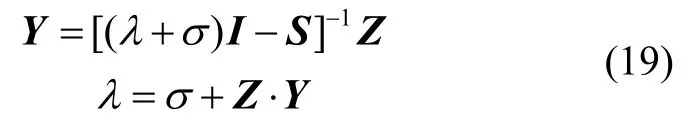
其中Y的定义为

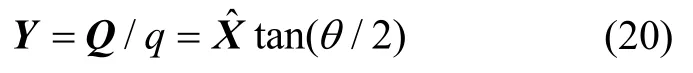
对应特征向量为

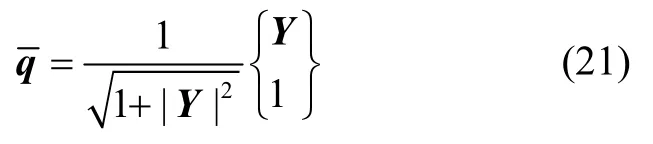
当λ取得最大值λmax时，Y与便可取得最佳姿态解Yopt与。由式(19)-(21)可以得到λ的表达式

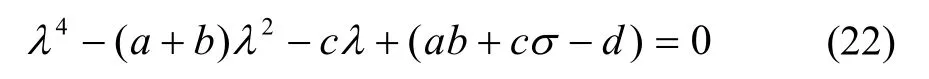
其中a=σ2- tr(adjS)，b=σ2+ZTZ，c= detS+ZTSZ，d=ZTS2Z。然后利用牛顿-拉夫逊算法对λ进行多次迭代求解，并将迭代的最终结果λmax代入到式（19）中，可以得到

其中X=（αI +βS+S2）Z。进而可以得到最优的姿态四元数结果

此时得到的四元数已无需进行归一化。再将结果转换为姿态矩阵代入式（1），即可得到实时的姿态角。

（2）算法优化

由（1）中的推导可知，只要观察记录同一个量在不同坐标系下的投影，即可得到两个坐标系之间的转换关系。因此我们用2.1节中的Gn（tN）与Gb（tN）分别代替QUEST算法中的与即可。

粗对准过程中，不同时刻计算得到的Gn（tN）或Gb（tN）均具有不同程度的误差，由式（10）可知，此时它们在算法中的权重ai应该是不同的。比较可靠的方法便是依靠“误差”的大小来对ai进行取值。

通过观察式（8）可以发现，式（8）的前半部分为t时间内里程计输出速度增量 ΔVod，理想情况下没有重力矢量信息的参与。后半部分为惯导输出的速度增量 ΔVimu，其中在竖直方向上的输出是有重力矢量参与引起的。二者相减再进行投影得到的便是重力矢量在b(0)坐标系下引起的速度变化 ΔVb。其原理如图2所示。

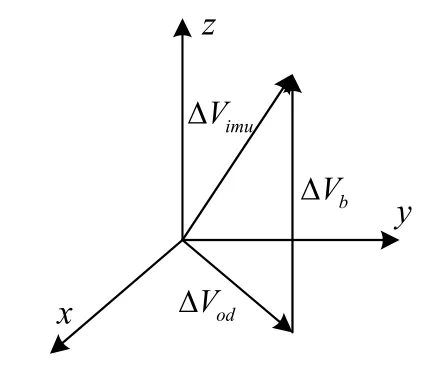
图2 b系天向速度增量的计算Fig.2 Calculation of Speed increment in vertical direction in body Frame

而式（9）相对简单，即T时间内重力矢量在n(0)坐标系下引起的速度变化。虽然重力矢量在不同坐标系下的投影不同，若忽略重力矢量的变化，其投影模值大小应等于重力矢量的模值。

基于以上分析，选择Gn（tN）、Gb（tN）与当地重力矢量在采样间隔时间T内积分模值的误差作为参数，定义误差函数

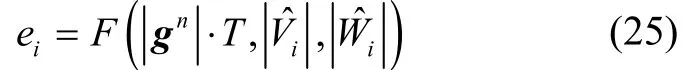
误差函数F可以根据实际效果调整。根据以上分析，首先提出一种误差计算方法：

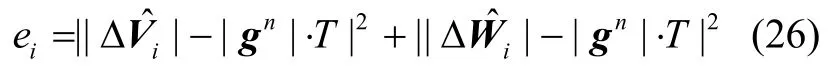
遵循ei与误差成正比的原则。然后对该计算方法进行分析验证。

图3、4为一次实验的姿态、速度变化与ei值随运动变化的情况。

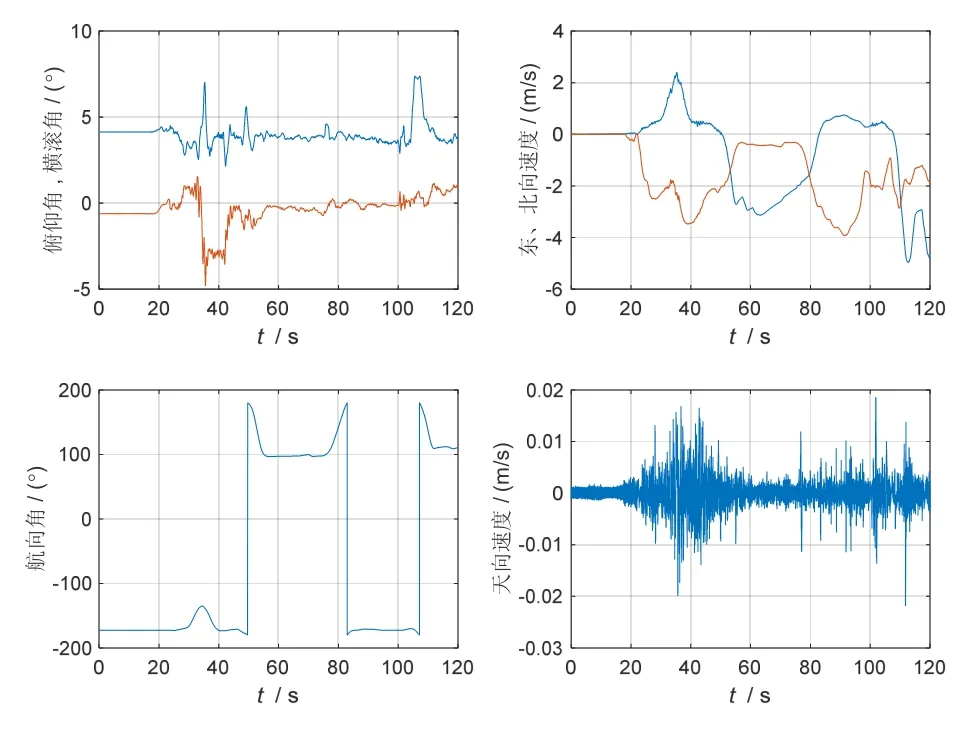
图3 姿态、速度变化曲线Fig.3 Curves of attitude and speed changing

由图3可以看出，在40 s左右时，水平姿态角变化较为剧烈，航向角稍有波动，反映到图4中即为ei值的增大，在110 s附近时，航向角变化剧烈，同样使得ei值变大。55 s到75 s以及85 s到105 s期间，尽管水平速度大小不同，但ei值总体保持平稳，仅在90 s处突然减速的瞬间产生了较高凸起。

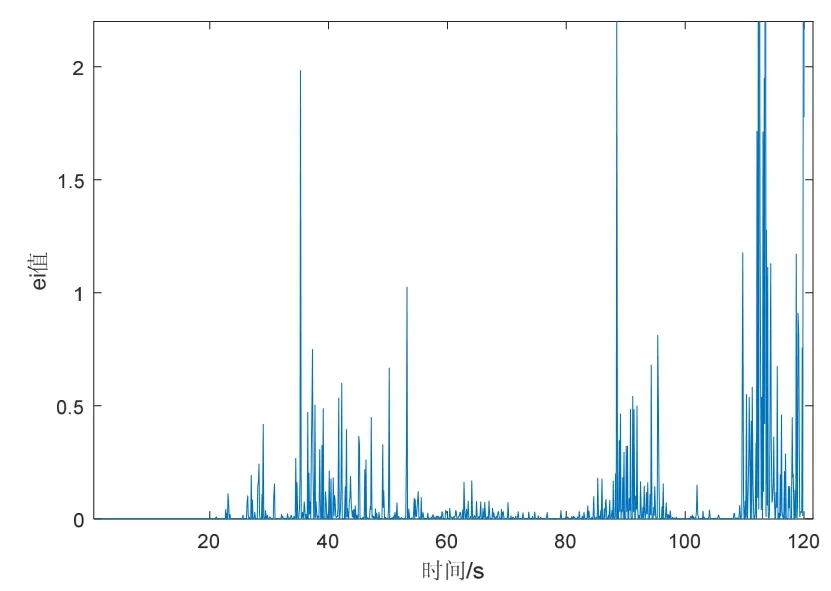
图4 值变化曲线Fig.4 Changing of

基于上述现象，再对式（8）（9）进行分析。式（9）中，的更新仅基于，与惯导里程计均无关，只要得到当前时刻的粗略姿态角结果，便可以结合里程计输出的速度计算得到，再将其补偿到中。的计算遵循公式(27)、(28)。

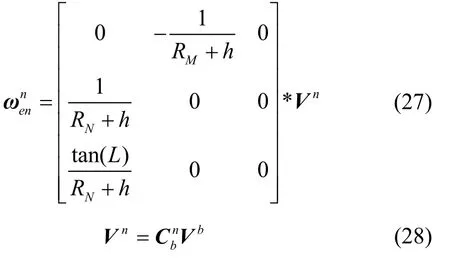
位置增量的计算遵循式（29）

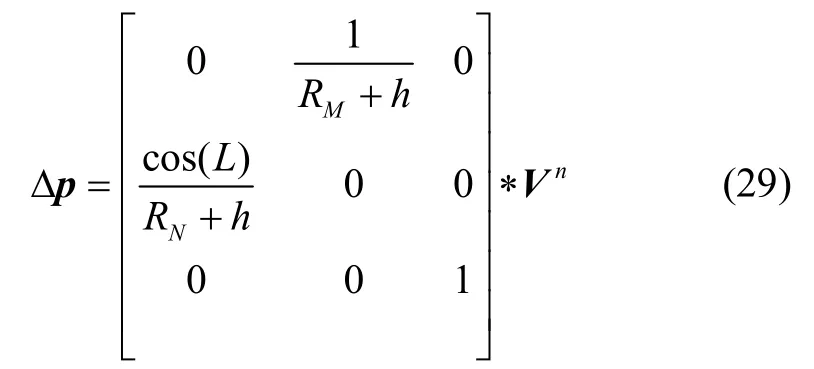
其中,L为当地纬度，RM与RN分别为子午圈和卯酉圈的主曲率半径，h为车载体的高程。

而式（8）中，--车体坐标系的更新依赖于陀螺仪的原始输出值，未经旋转、划桨效应等补偿，在姿态变化剧烈时会存在较大误差，--车体速度由里程计测得，路况以及突然启动或停止时都会对测量值造成一定的影响。

由此可见，对于QUEST算法来说，水平速度的大小相较于姿态角波动而言对算法的稳定性影响较小，但当加速度较大，如突然启动或停止时同样会造成较大影响。这与图3，4的实际测试结果相吻合，证明ei值可以很好地反映各时刻信息的误差大小。

根据ei大小可对信息的权重进行取值。当误差较小时，ai值可按比例取为较大值或1，使得当前时刻信息得到较完整保留。而当某一时刻误差很大时，ai值可以根据误差大小取较小值或取为0，减弱当前时刻信息对整个对准过程的影响。经实验验证，可有效减弱误差较大信息的影响。

3 实验结果分析

3.1 仿真实验

基于MATLAB平台设计了两条仿真线路，初始姿态为[4；0；98]（俯仰，横滚，航向角/°），每条线路均进行5组测试。线路方案以及陀螺、加表参数分别列在表1与表2中。

表1 线路方案Tab.1 Route plans

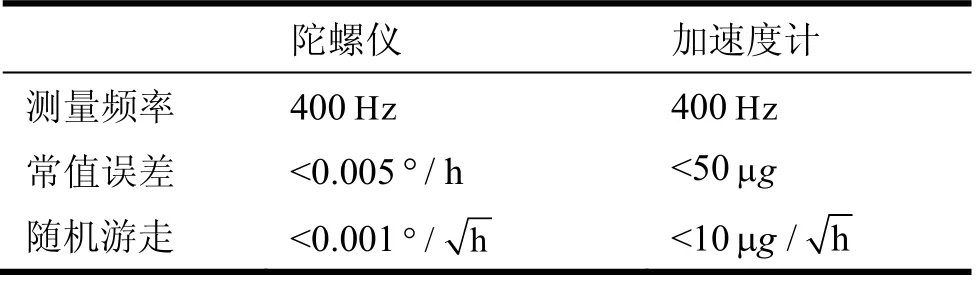
表2 陀螺仪和加速度计基本参数Tab.2 Basic parameters for gyroscopes and accelerometers

表3中分别给出了两条线路的粗对准姿态角误差。

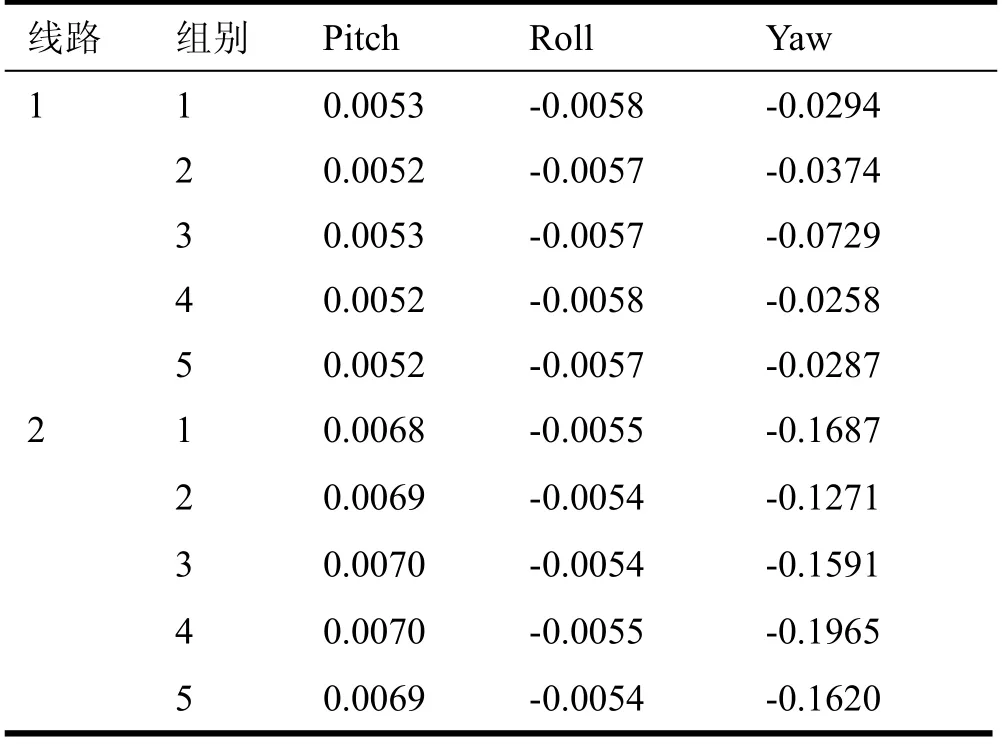
表3 粗对准误差（单位：°）Tab.3 Coarse alignment errors(°)

从线路1实验结果可以看出，本文提出的动基座粗对准算法在静基座条件下，粗对准航向角小于0.06 °，同样保持了较高的精度。从线路2的实验结果可以看出，当车载体运动时，粗对准结果略有下降，但仍然保持较高的精度水平。

基于线路2，给出了使用未经优化的算法与优化后算法的粗对准效果对比,如图5所示。

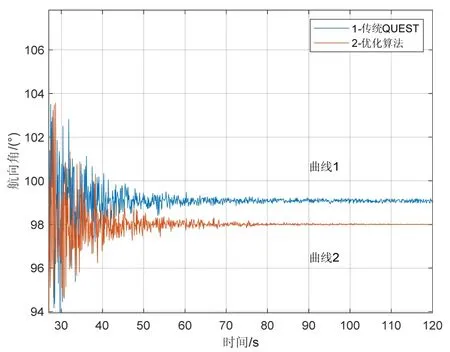
图5 航向角粗对准精度对比Fig.5 Comparison of yaw angle accuracy

图5结果表明，仿真条件下，使用经过优化改进后的算法，可以有效地提高粗对准的精度。

3.2 车载实验

采用某激光陀螺双轴转位惯性导航系统，固定于车载体之上，配合已标定好的里程计，进行了四组车载实验。实验设备布局如图6所示。

图6 车载实验设备构成Fig.6 Equipment arrangement in on-vehicleroad tests

实验路线如图7所示。实验路线全长约1.5 km，包含急转弯，长直路段。出发前首先静止1分钟，前半程位于校内，速度较慢，60 s左右进入公路（（-250，-60）坐标处），开始加速行驶。

跑车结束后进行了静基座对准，得到一组实验车载体的姿态角[3.864;1.013;8.385]（单位：°）。图6给出了一组实际测试中航向角收敛过程。

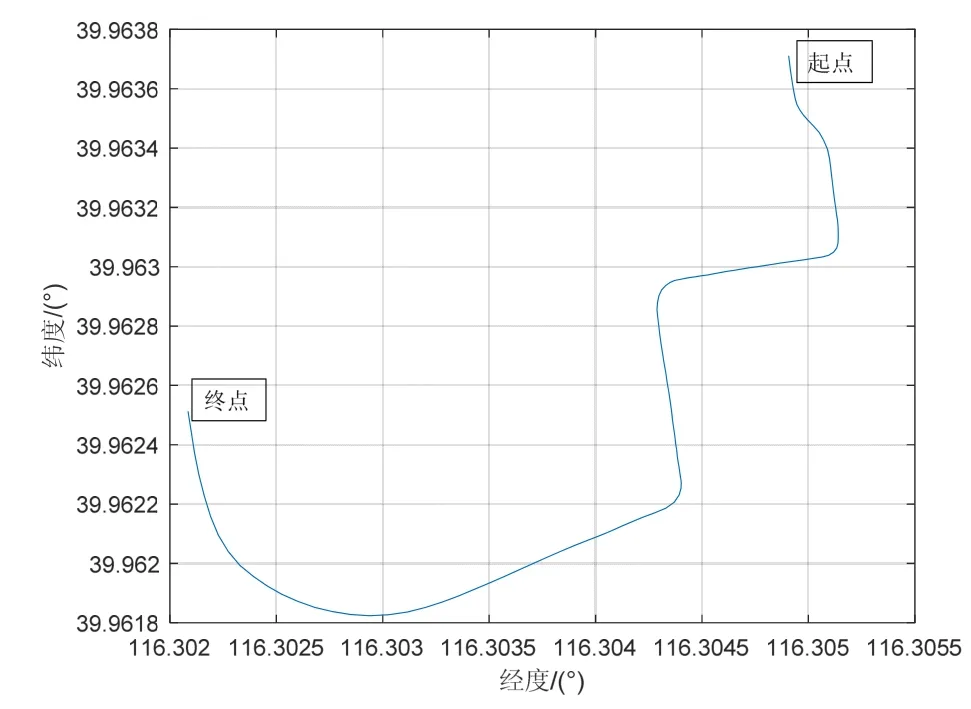
图7 实验路线Fig.7 Road testroute

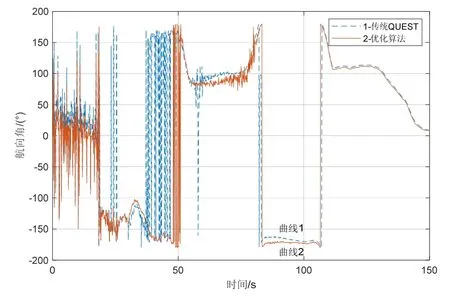
图8 实际测试中航向角变化曲线Fig.8 Changing of yaw angle in road tests

从图8中可以看出，在40 s到50 s转弯处，85 s及105 s转弯处，以及60 s进入长直路段加速处，本文中的优化算法相对于传统的QUEST算法，适应性更高，能够有效减少因误差较大的信息造成的波动，且粗对准精度较高，表4中给出了全部四组车载实验的粗对准算法对比情况。

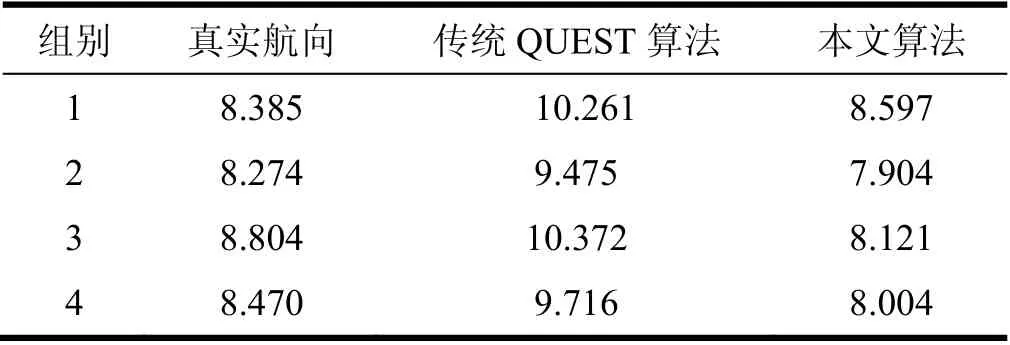
表4 车载实验粗对准算法对比（单位：°）Tab.4 Comparison of the coarse alignment algorithm in road tests(°)

从图7，8和表4可以看出，在实际应用中，该粗对准算法对路况以及速度的变化有较强的适应性，并且有效减弱了误差较大信息的影响，保持较高的对准精度，在150 s内航向角误差已经缩小到 ± 2°范围内，完全满足精对准需求。证明该算法具有很好的实用性。

4 总 结

本文提出了一种基于里程计辅助的QUEST优化算法。由于小量的忽略和误差的累积，每个时刻的信息权重并不相同，因此采用了与重力矢量之间的模值误差为权重参考，并进行实时反馈修正，减小误差影响。最后设计多次试验，证明了该算法的准确性以及对于实际应用中车载体运动的适应性。从实验结果可以看出，该算法可以实现车载体行进间的粗对准，适应性较强，能够得到较高精度的姿态估计。