基于MODIS数据计算的RLPM模型在黄土高原地区的应用

刘 宁，崔晨风，翟羽婷

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

蒸散发(ET)被称为作物需水量，是科学研究人员研究区域水安全和判断水资源供水关系是否紧张的理论基础，也是行政机构进行水资源配置和水环境供需安全的判定依据[1]。因此如何进行蒸散发精准计算对研究节水灌溉和旱区水资源高效利用等有着十分重要的现实意义和深远影响，也是研究农作物用水与提升用水效率的一项重要工作[2]。人类对于自然科学的认识愈加深刻，同时也不断突破农业科学研究领域，所以对于蒸散发反演的研究计算已经取得了一系列具有里程碑利益的科研成果。

2010年Mu等人改进了基于MODIS卫星数据的全球地面蒸散发算法[3]后续团队通过卫星遥感技术获取的叶面积指数开发了一系列用于计算部分植被覆盖时的地表导度。例如Helen[3]采用16 d过境一次的MODIS数据经研究后提出了一个新的地表导度反演公式。在前人研究基础上，Leuning和Zhang[4]等人改进方法提出了一个更高效的地表导度反演计算公式，然后将该ET反演模型在全球15个具有不同下垫面情况和气候类型的研究区域进行ET值反演验证计算，结果表明该地表导度反演模型用于蒸散发的估算具有很高的精度。但目前的研究当中，卫星遥感数据分辨率依旧太低，反演精度有待进一步提高。

因此本文基于FAO56[5]提出的Penman-Monteith数学模型，结合Leuning提出的叶面积指数(LAI)反演ET的理论思想，提出Remote Sensing Leaf Area Index Penman-Monteith模型(RLPM)，并使用地理空间数据云提供的TERRA卫星MOD09GA经过拼接、切割、投影转换、单位换算等过程加工而成的MODIS中国合成产品NDVI和研究区气象资料数据反演出所需的参数值，最后可计算研究区域内任意时间、任意地点的日ET值。选择黄土高原作为研究区域，对模型的有效性进行验证，发现其适用性和应用性较好,精度较高。

1 研究区概况和研究方法

黄土高原位于半干旱向干旱过渡带地区，气候具有显著突出的过渡性基本特点，属于半干旱暖温带大陆性季风气候。流域内年降雨量为300～700 mm，多年降雨量的平均值大约为450 mm，总的趋势是从东南向西北递减。根据季节的变化，降水分配不均，空间分布为南多北少，东多西少，主要集中在夏季7、8、9这3个月，并且常常与暴雨的形势出现，雨量占全年的70%～80%，大部分地区干旱少雨，水资源十分匾乏。黄土高原区域河网密度较小，水力资源不足，一级河流有黄河，是陕西与山西的边界河，流经三门峡市、运城市、延安市、吕梁市等城市。研究区的二级流域包括汾河、渭河、泌河、南洛河等河流。但由于年降水量随季节的时空分配不均，各级河流年径流量的季节分配有一定的差异，夏季的年降水量更集中，本流域的洪水期基本在7-9月，在这以后季风将会开始南退，降水稀少，进入枯水期，12月份径流量最小，部分河流受温度影响存在结冰期。在夏季降水量增大，进而引起山洪暴发，造成水土大量流失，农田涝灾。

本文选用的气象数据来自于中国气象数据网地面资料的中国地面气候资料日值数据集(V3.0)中，以北纬34°～ 40°东经103°～ 114°为研究区界线，分布在黄土高原及其周边98个国家气象站点所收集的数据。研究时间设为2010-2015年，使用气象资料站点最高和最低气温、相对湿度、风速等。

将选用的遥感数据分成2类：第1类是地理空间数据云(http:∥www.gscloud.cn/)提供的GDEMV2 30 M分辨率数字高程数据；第2类是地理空间数据云提供的MODND1D 我国 500 MNDVI每天数据集。

技术路线见图1。

2 RLPM反演模型

2.1 RLPM计算公式[6]

(1)

式中：λ为汽化潜热物理量，MJ/kg；ER为遥感反演蒸发蒸腾量，mm/d；ε为辅助计算数，ε=Δ/γ；A为太阳光照射后可用能量，MJ/(m2·d)；ρa为实时空气密度，kg/m3；Cp为空气常压下的比热容，1.013×10-3MJ/(kg·℃)；γ为湿度计系数，kPa/℃；Da为参考高度饱和水汽压强差，kPa；Ga为空气动力传导度，根据所在研究区土地利用类型，因该因素对RLPM反演结果不敏感，所以将树木、草地与农作物的空气动力传导度分别设为0.033、0.012 5、0.010[7]；Δ为气温T下的饱和水汽压曲线系数，kPa/℃；Gs为地表传导度。

植株蒸腾和株间蒸发这2部分组成遥感反演蒸散发量，因此本研究采用遥感数据先行反演计算这2部分各自的蒸发量，然后相加得到该研究站点的反演值：

ER=ERc+ERs

(2)

式中：ERc为利用可用能量A中的冠层吸收能量Ac计算得出的植株蒸腾量，mm/d；ERs为利用可用能量A中的土壤吸收能量As计算得出的株间蒸发量，mm/d。

(3)

(4)

式中：Gc为冠层叶面气孔最大时的冠层传导度；Ac为A中被植被冠层所收集的太阳辐射，MJ/(m2·d)；As为A中被下垫面土攘所收集的太阳辐射，MJ/(m2·d)。

2.2 RLPM模型参数计算过程

2.2.1 冠层吸收能量和土壤吸收能量

养老金作为一种基本的养老保障制度，关乎着每个人能否享有一个安乐的晚年生活，决定着一个人的幸福感是否可以得到满足，代表着一个国家的基本保障制度是否完善，甚至关乎着我国社会的长治久安与和谐稳定。在我国，养老金一直是人们所关注的焦点问题。尽管通过多年的研究，到现在我国已初步建成了世界上最大的养老保障体系，基本上覆盖了所有人群，但是我国养老金仍然面临着很大的困局。

(5)

(6)

τ=exp(-kALAI)

(7)

式中：kA是可用辐射衰减系数，设定为0.6；LAI为叶面积指数，由归一化植被指数(DNVI)求得，NDVI数据信息的来源是地理空间数据的MODND1D 中国 500 MNDVI每天产品获得。

2.2.2 辅助计算参数

ε=Δ/γ

(8)

(9)

(10)

式中：Δ为气温T下的饱和水汽压曲线系数，kPa/℃；Tmean为日平均温度，℃；Exp是指数函数，底数为2.718 3；P为大气压，kPa；Cp是空气常压下的比热容，1.013×10-3MJ/(kg·℃)；ε1为水蒸汽分子量与干燥空气分子量的比值，其值为0.662；其余符号意义同前。

2.2.3 实时空气密度

理想气体方程为：P=ρRT。地表上方的空气含有一定的水分，水分会随着压强、温度等因子发生动态变化，导致实际空气密度也会随之变化，故实时空气密度ρa计算公式如下：

(11)

式中：Rd为干空气的比气体常数，0.287 J/(g·K)；ea为实防水汽压，kPa；其余符号意义同前。

2.2.4 汽化潜热常数

λ=2.501-(2.361×10-3)Tmean

(12)

Da=e(Ta)-ea

(13)

(14)

(15)

(16)

(17)

式中：ea是实际的水汽压强，kPa；eO(Tmax)是在日最高气温时的饱和水汽压强，kPa；eO(Tmin)为在日最低气温时的饱和水汽压强，kPa；RHmax为日最大相对湿度，%；RHmin为日最小相对湿度，%；Tmax为每日最高气温，℃；Tmin为每日最低气温，℃；其余符号意义同前。

2.2.6 可用能量

A=Rn-G

(18)

式中：Rn是净辐射，MJ/(m2·d)；G是土壤热通量，MJ/(m2·d)。

2.2.7 土壤热通量

土壤热通量可用复杂的模型描述。本研究的样本时间尺度均为日尺度，所以土壤热通量非常小，可以忽略，因此本研究令G≈0。

2.2.8 净辐射

净辐射Rn是进来的净短波辐射Rns与出去的净长波辐射Rnl的差值：

Rn=Rns-Rnl

(19)

Rns=(1-α)Rs

(20)

(21)

式中：Rns为净太阳或短波辐射，MJ/(m2·d)；α为反射率或冠层反射系数，以草为假想的参考作物时，α值为0.23；Rs为射入进来的太阳辐射，MJ/(m2·d)；n为太阳持续照射时间，h；N是最强太阳持续的照射时长，h；Ra为天顶辐射，MJ/(m2·d)，计算公式可以参照FAO-56；as为回归常数，在研究区地表所吸收的、有云时的太阳天顶辐射，as=0.25；as+bs为研究区地表所吸收的、全部的太阳天顶辐射，bs=0.50。

2.2.9 植被的冠层传导度

(22)

式中：kQ为短波辐射的衰减常数，设定为0.6；kA为可用太阳辐射的衰减系数，设为0.6；Qh为植被冠层上方的太阳辐射通量，QH=0.8A；Q50为气孔导度gs=gsx/2(gsx为gs的最大值)时的太阳辐射通量，设为2.6 MJ/(m2·d)；D50为气孔导度gs=gsx/2(gsx为gs的最大值)时的实际估算的水汽压差，设为0.8 kPa。

LAI为叶面积指数，采用NDVI转换公式[8]求得，详细计算公式[9]见表1。

表1 归一化植被指数(NDVI)转换为叶面积指数(LAI)的计算公式[10]

3 RLPM模型在黄土高原的应用

本文基于FAO56提出Penman-Monteith模型，结合Leuning提出的叶面积指数(LAI)反演ET的理论思想，提出Remote Sensing Leaf Area Index Penman-Monteith模型(RLPM)，并使用地理空间数据云提供的TERRA卫星MOD09GA经过拼接、切割、投影转换、单位换算等过程加工而成的MODIS中国合成产品NDVI和研究区气象资料数据反演出所需的参数值，最后可计算研究区域内任意时间、任意地点的日ET值。选择黄土高原作为研究区域，对模型的有效性进行验证，发现其适用性和应用性较好，见图2。

图2 黄土高原归一化植被指数反演图

3.1 部分参数的频数图

以2013年的黄土高原研究区日数据为例，对部分地表物理参数和气象参数的计算结果进行统计分析(见图3～图8)。频数曲线图均为单峰曲线且平缓变化，表明研究区下垫面整体情况均匀变化，差异不显著。NDVI主要分布范围为0～0.2，符合黄土高原植被稀少的实际情况。湿度频数图中间高，两边低，主要分布在0.4～0.6。净辐射主要分布范围为2～8 MJ/(m2·d)，在2个支出项中，土壤吸收的能量最多，远超于植被吸收的能量。

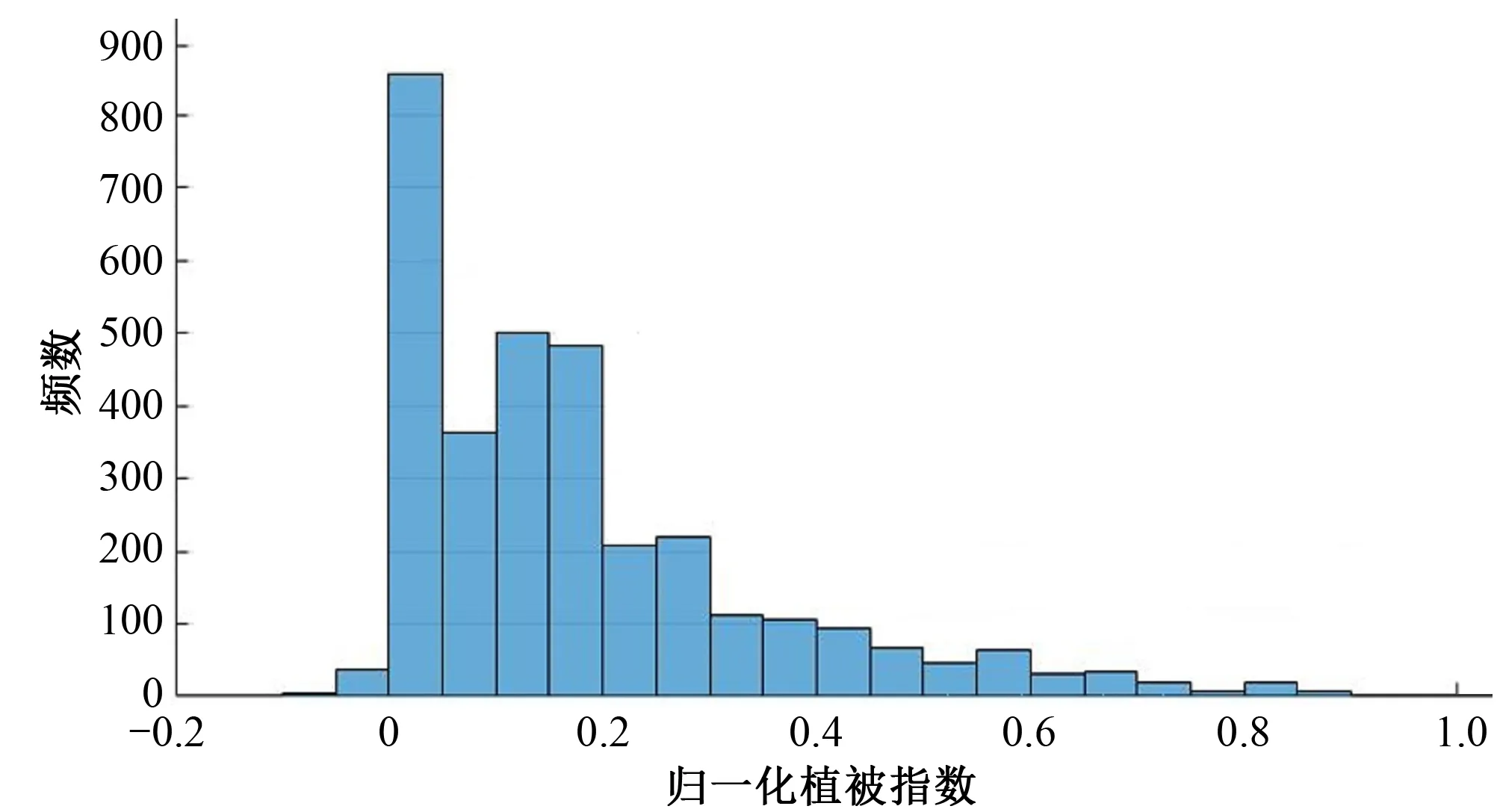
图3 归一化植被指数频数图

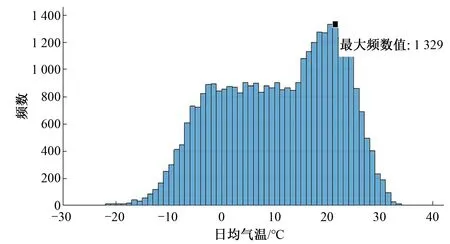
图4 日均气温频数图

图6 日净辐射频数图

图7 冠层吸收能量频数图

图8 土壤吸收能量频数图

3.2 RLPM模型相关性分析

为研究RLPM模型反演结果的准确性和可靠性，本研究采用Penman-Monteith公式(Richard G Allen 1998)计算同时间、同站点的ET值，并列为真实值，从而得到研究区的日蒸发蒸腾量，再根据遥感数据NDVI反演得到的蒸发蒸腾量反演ET值进行比较验证，根据线性拟合公式分析2者的线性相关程度。分析结果见图9～14。

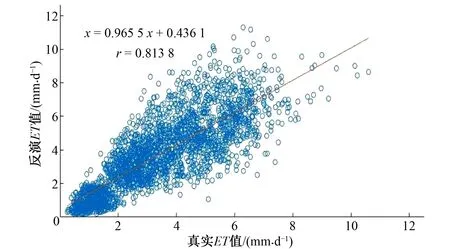
图9 2010年数据相关性分析图

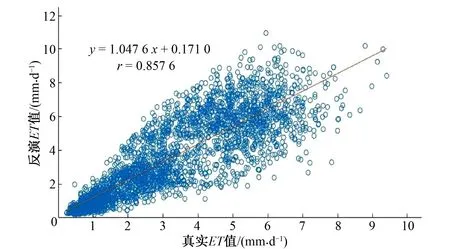
图10 2011年数据相关性分析图

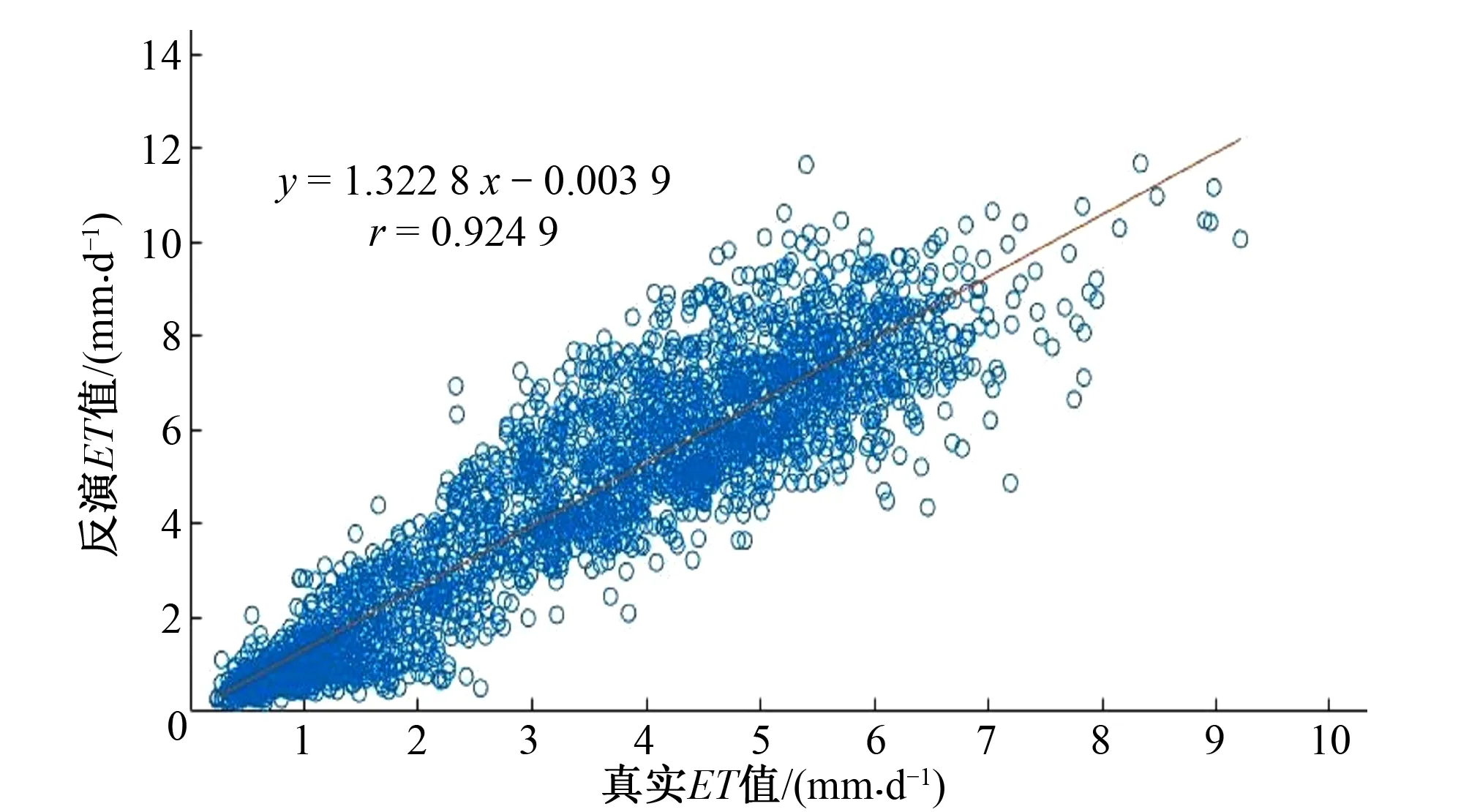
图11 2012年数据相关性分析图

图12 2013年数据相关性分析图

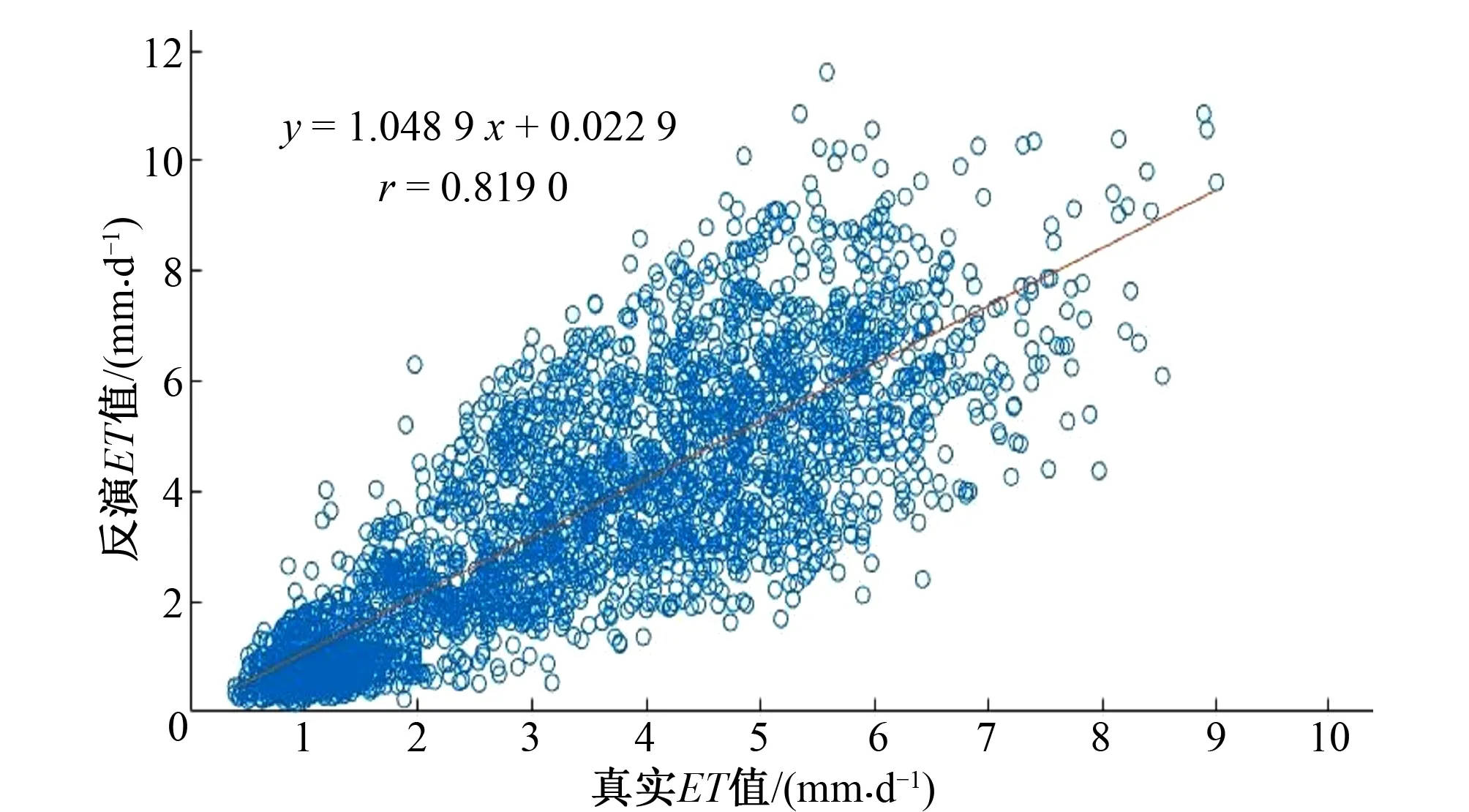
图13 2014年数据相关性分析图

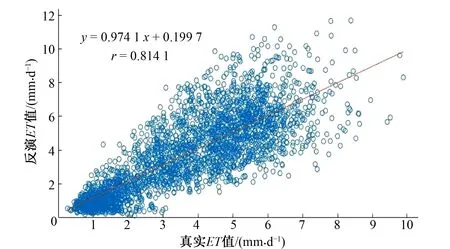
图14 2015年数据相关性分析图

如图9～14，收集98个站点的2010-2015年每月5号、15号、25号的数据，每年大概3 000 多份有效的数据样本，总共18 000 份样本数据进行分析。y轴为根据RLPM模型计算出来的反演ET值，x轴为根据P-M公式计算出来的真实ET值，对2者进行归一性相关分析，相关系数计算公式如下：

式中：r的范围为[-1，1]。|r|值越大，变量之间的线性相关程度越高；|r|值越接近 0，变量之间的线性相关程度越低。一般可按3级划分：|r|<0.3 为低度线性相关；0.3≤|r|<0.8为显著性相关；0.8≤|r|<1.0为高度线性相关。采用MATLAB进行代码运算，得到2010-2015年反演值与真实值的相关系数(见图9～14)。根据相关性分析结果，所有r均大于0.8，最低值为0.813 8，其中2012年的相关系数最高，为0.924 9。

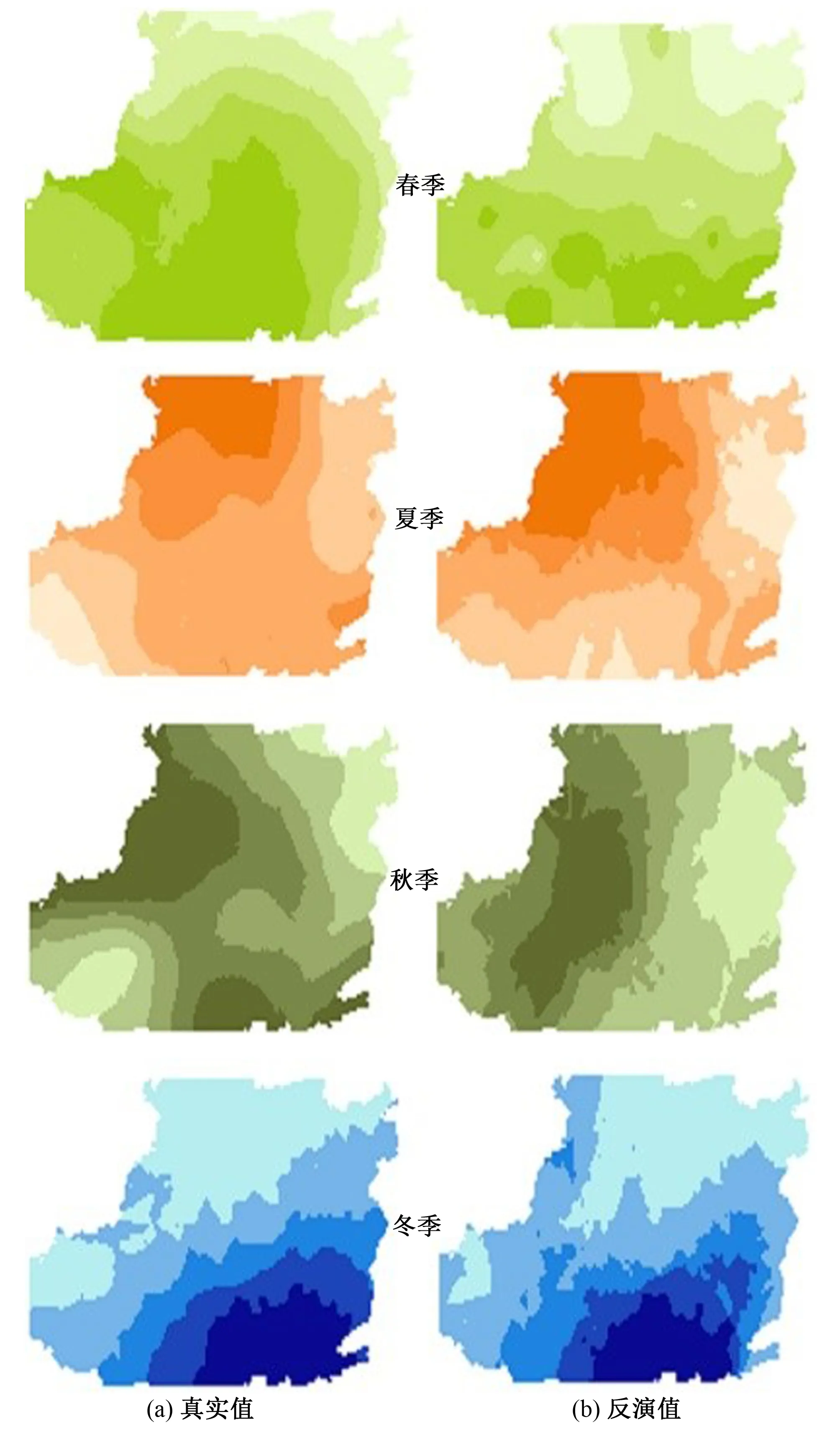
图15 不同时期ET真实值与反演值对比

图15(a)为使用P-M公式计算出来的真实ET值所构成的图像，图15(b)为采用RLPM模型反演的ET值所构成的图像。以黄土高原为研究区域，分别选择春夏秋冬四季中的一天进行对比分析。其中，第1个对照组时间为2013-02-15，第2个对照组时间为2013-06-25，第3个对照组时间为2013-08-15，第4个对照组时间为2013-11-05。根据ET值变化趋势来看，RLPM模型反演ET值与采用彭曼公式计算所得结果的相关性高。

4 总 结

本文采用的研究方法是MODIS卫星遥感数据和地面气象数据的结合，把黄土高原作为研究地区，由于该地区气候和下垫面土地利用类型的剧烈变化，所以基于Remote Sensing Leaf Area Index Penman-Monteith模型，采用研究区域内2010-2015年的98个观测站点所得气象、水文和遥感数据为基础进行区域蒸散发量反演。收集整理了黄土高原整个研究区2010-2015年的逐日卫星遥感数据图，采用RLPM模型进行蒸散发的反演，同时采集了研究区98个气象站2010-2015年的逐日地面气象数据。采用FAO 56 Penman-Monteith 计算了各个站点的实际蒸散发量(ET)值。对2组数据进行对比分析发现2组数据的相关系数大于0.8，呈高度线性相关。反演计算所得ET值与ET真实值相比较，发现整体上反演值的变化趋势和最大最小值发生时段都贴近真实值，并且反演值所得曲线比较平滑。

由此可见，RLPM模型在黄土高原区域ET反演精度较高，应用性强。