基于激光雷达的树形靶标冠层叶面积探测模型研究

谷趁趁 翟长远 陈立平 李 琪 胡丽娜 杨福增

(1.西北农林科技大学机械与电子工程学院， 陕西杨凌 712100； 2.北京农业智能装备技术研究中心， 北京 100097；3.国家农业信息化工程技术研究中心， 北京 100097)

0 引言

果园农药喷施是果树生长过程中重要的管理环节[1-4]，约占果树生产管理作业量的30%，可以减少60%～90%的果品损失[5]。传统病虫害防治普遍采用连续无差别喷药，农药利用率低(20%～30%)，造成环境污染和果品农残超标等问题[6-9]。精准变量喷药技术能够有效解决传统喷药中存在的问题，通过传感器探测靶标位置、几何尺寸、体积和枝叶稠密度等信息进行精准和变量作业。目前已经实现基于果树冠层位置、体积等的变量喷药技术[10-15]。但在果树整个生长周期中，果树冠层体积变化较小，冠层内树叶稠密度变化较大，相同冠层不同区域内树叶分布的稠密度差异较大。喷雾作业过程中，有效喷雾为单位面积(cm2)叶片上沉积雾滴个数大于等于20个，雾滴覆盖率大于等于33%[16]。果树冠层内叶面积的有效探测能够在变量喷雾过程中为喷雾量计算提供有效依据。在现有靶标探测基础上研究靶标内稠密度探测方法，构建探测模型可为变量喷雾控制提供数学模型支撑。

靶标冠层稠密度衡量指标主要有冠层生物量、叶面积指数(Leaf area index,LAI)、叶面积密度(Leaf area density,LAD)和叶面积(Leaf area,LA)。果树冠层内树叶稠密度在立体空间内分布具有随机性、不可预测性，存在定量分析难的问题。目前针对冠层稠密度探测研究，主要采用超声波传感器[17-19]和激光雷达(Light detection and ranging,LiDAR)传感器[20-25]。但是超声波在靶标探测过程中存在探测延迟和易受外界环境影响等问题，难以在实际中应用。LiDAR传感器发射的激光束具有高能量密度、较小的分散角和较远直线传播距离等优点，可被应用于果树冠层枝叶稠密度探测研究[26]。通过LiDAR研究冠层几何参数与冠层LA、LAI之间的相关关系，间接获取LiDAR与冠层稠密度之间的关系，计算过程复杂[20-22]。文献[23]分别针对实验室小榕树和现代矮化种植墙式苹果树研究LiDAR点云数据与冠层LA之间的关系，得出小榕树和果树不同生长时期冠层LA与LiDAR点云数据存在线性回归的关系。由于研究果树冠层为墙式冠层，厚度小且厚度均匀，对果树冠层厚度大且不均匀冠层的LA关系模型的适用性有待进一步验证。文献[24]通过LiDAR获得了人工仿真树的点云数据，用点云个数与冠层LA进行多项式拟合，获得LA计算方程。冠层厚度和冠层体积直接影响探测模型的准确性，该研究忽略了冠层厚度或冠层体积等三维空间参数的影响。文献[25]采用简单的回归算法研究LiDAR点云数据与冠层叶面积、冠层体积与冠层叶面积之间的相关性。研究中没有考虑叶面积空间分布的特点，指出需要引进更优算法以提高果树冠层叶面积计算精度。

偏最小二乘回归(Partial least squares regression,PLSR)算法和BP(Back propagation)神经网络算法在回归分析过程中，能够显著提高模型的预测精度。基于PLSR分析之前，首先对数据集进行主成分分析降维。计算过程中对自变量和因变量分解的同时提取因子，将影响因子按照相关性从大到小排列，可以减弱自变量间的冗余性[27]。该方法是结构方程模型的一种形式，不同于基于协方差的经典计算方法[28]，能够根据较少的因素给出最优的预测结果[29]。BP神经网络回归算法具有多层网络结构(大于等于3层)，每层由若干神经元组成。使用最速下降法，反向传播调整网络权值和阈值，使网络的误差平方和最小[30]。

针对精准变量喷药技术中，冠层叶面积探测对有效计算施药量影响较大，现有叶面积探测研究多基于典型回归算法获得，模型简单，存在拟合精度低等问题。本文基于LiDAR点云数据和冠层厚度的叶面积探测模型，采用PLSR算法和BP神经网络算法进行建模，以期为精准变量喷雾技术提供有效的叶面积探测模型支持。

1 材料与方法

1.1 三维立体试验平台

为了测量并计算立体空间冠层内叶面积，设计三维立体试验平台(图1)。该试验平台由前、后网格架，网格支架，网格线和网格分界线组成。前后网格架尺寸(长×高)为4 m×1.5 m，前后网格架固定间距为3.5 m，网格支架高度为0.57 m。网格架设置张紧装置，用于张紧网格线，防止网格线松散。网格尺寸通过调整网格线设置为0.1 m×0.1 m的正方形。网格分界线连接前后网格架对应网格区域，实现立体空间网格区域确定。

1.2 LiDAR探测移动平台

为了获取靶标冠层LiDAR点云数据，搭建LiDAR探测移动平台，应用LiDAR传感器对靶标冠层进行扫描。试验平台由移动平台架、步进电机(86HB250-80B型，鸿宝达)、步进电机驱动器(HB860H AC18-80V型，鸿宝达)、步进电机控制器(KH-01型，路易马丁)、步进电机电源、便携式计算机(T470p型， 联想)、滑动导轨(W40-03 型，CCM)、LiDAR传感器(LMS10100型，Sick)和LiDAR电源等组成(图2)。设定LiDAR扫描频率50 Hz，角度分辨率0.5°。LiDAR在试验平台上最大移动距离为5 m，探测速度为0～1.4 m/s，平台高度1.5 m。LiDAR与计算机通过网口连接，增加数据传输效率。

1.3 三维立体空间树形靶标冠层布置及叶面积计算方法

1.3.1树形靶标冠层布置

试验在北京市昌平区小汤山国家精准农业研究示范基地进行。试验树采用与苹果树叶叶形相似的仿真树叶。3个叶片为一组，试验采用单组树叶和双组树叶组合的布置形式(图3)。

树形靶标冠层布置为稠密和稀疏2种稠密度。稠密冠层布置叶片组间距为10 cm，布置形式如图4所示，并以单双交替的形式布置在每条网格线上。稀疏布置叶片组间距为20 cm，布置形式见图5。靶标冠层厚度布置为1.2 m和1.4 m。计算布置树形冠层稠密和稀疏的LAD为0.114 m2/m3和0.057 m2/m3。符合实际测量的苹果树冠层稠密区域密度0.1～0.15 m2/m3和稀疏区域冠层密度小于等于0.06 m2/m3。对冠层4种布置形式(稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层)进行试验研究。

对树形靶标布置，将前后网格架用网格线连接，在网格架内按上述形式布置叶片。网格线选用直径1 mm的透明尼龙线，尽量减少对LiDAR点云数据获取的影响，该线耐拉扯且不易断裂。树形靶标(稠密厚冠层)布置如图6所示。将树形靶标冠层布置为规则形状，冠层宽度0.99 m，高度1.06 m。

1.3.2树形靶标叶面积计算方法

试验过程中，叶面积的计算方法分为3个步骤。首先，人工统计靶标冠层不同区域中叶片数量；然后，采用叶面积测量仪(山东方科仪器有限公司，YMJ-G型)测量20组仿真树叶叶面积，计算仿真树叶的平均叶面积为25.26 cm2；最后，通过叶面积与叶片数的乘积计算每个网格区域中叶面积。试验过程中，首先布置稠密树叶，统计叶片数量，用LiDAR扫描仿真树，获得点云数据，测量完成后在不改变冠层外形尺寸的情况下，进行不同冠层厚度和稀疏叶片布置(图5)，测量冠层中叶片数量，并进行试验研究。

1.4 LiDAR点云数据获取与处理

LiDAR通过滑轨沿移动平台移动，扫描树形靶标，获得靶标冠层LiDAR点云数据。原始LiDAR点云数据为极坐标形式，研究中需通过坐标转换将数据由极坐标转换为笛卡尔坐标。通过LiDAR激光束与水平方向和垂直方向的夹角结合点云极坐标，计算激光束在笛卡尔坐标系中x、z2个方向的坐标值，LiDAR在滑轨上的移动距离为y方向坐标值。将转换为笛卡尔坐标的LiDAR点云数据网格化处理，分别沿y方向和z方向划分网格。设定网格区域尺寸为0.1 m×0.1 m，计算网格区域中LiDAR点云数(N)，将LiDAR点云数据沿x轴方向探测距离与冠层厚度进行差值计算，获得探测不同位置的冠层厚度，提取0.1 m×0.1 m网格区域中x方向冠层最大值作为该网格区域冠层厚度(L)。

1.5 关系模型回归分析

分别构建不同冠层稠密度和冠层厚度条件下，LiDAR点云数和冠层厚度与叶面积之间的探测模型。采用PLSR和BP神经网络回归算法，进行回归分析。

PLSR算法对数据进行回归分析过程中，对原始数据中自变量(LiDAR点云数和冠层厚度)和因变量(叶面积)标准化后，提取变量组的第一主成分并建立变量组，进行主成分回归。通过残差矩阵替换重复数据主成分回归，获得数据回归方程。采用验证集数据对回归方程进行交叉验证，预测模型精度和可行性。

根据数据格式设置BP神经网络为2-3-1的网格结构，即2个输入层、3个隐藏层和1个输出层。确定隐藏层节点数的基本原则为，在满足精度的前提下,选取尽可能紧凑的结构，即隐藏层节点数尽可能少，节点数p必须小于M-1(M为训练样本数)。计算过程中选择newff函数中trainlm函数的Levenberg-Marquardt(LM)算法创建BP神经网络，该算法为BP神经网格学习训练的默认函数，具有对于中等规模网格训练速度最快的优点。

2 试验

2.1 仿真树冠层点云图

使用LiDAR探测移动试验平台和叶面积三维立体试验平台完成树形靶标扫描。按照上述数据处理方法，对数据坐标进行转换，获得树形靶标原始点云图(图7)。观察图7可见，获得的靶标冠层点云图与图6a树叶分布较一致。

通过数据处理，获得不同区域的LiDAR点云数(N)和冠层厚度(L)，并与人工测量不同区域的叶面积对应。试验研究中获得稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层4种情况下各42组数据。图8为获得的冠层原始数据散点图。观察图8得出，冠层越稀疏、厚度越小获得的散点图分布范围越小。4种情况获得的LiDAR冠层点云数据按照稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层逐渐减少，说明冠层稠密度和冠层厚度不同获得的LiDAR点云数据不同。观察4种冠层的散点图，获得点云数据的冠层厚度坐标小于等于1.2 m，说明激光束在穿透稠密厚冠层和稀疏厚冠层过程中，在冠层厚度1.2 m的范围内被截获，没有到达冠层厚度1.4 m处，但是可以到达稠密薄冠层和稀疏薄冠层。

2.2 基于PLSR算法的冠层叶面积探测模型

采用PLSR算法研究不同冠层稠密度和不同冠层厚度条件下叶面积探测模型，计算过程中将获得的42组数据以5∶2的比例分为测试集和验证集，测试集30组，验证集12组。通过测试集计算获得叶面积的多元回归探测模型，用验证集验证模型的准确性。

图9为不同冠层稠密度和冠层厚度条件下，通过测试集获得函数方程的拟合图。通过观察图9a、9c与图9b、9d真实值与预测值拟合效果，得出稠密冠层拟合方程对预测值的拟合效果明显优于稀疏冠层，说明冠层树叶稠密度对叶面积影响较大。对比图9a与图9c以及图9b与图9d得出，冠层厚度对叶面积探测模型的影响较小。

通过PLSR算法获得不同树形靶标叶面积探测模型，具体公式为

y1=-56.58+1 211.12L1-0.06N1

(1)

y2=-260.840+1 089.78L2-0.277N2

(2)

y3=-332.985+922.60L3-0.014N3

(3)

y4=18.357+239.73L4-0.147N4

(4)

式中，y1、y2、y3和y4为稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层条件下探测模型的叶面积。L1、L2、L3和L4为不同冠层的厚度，N1、N2、N3和N4为不同冠层LiDAR点云数。

用验证集对叶面积探测模型的准确性进行验证，通过输入验证集中冠层厚度和LiDAR点云数计算冠层叶面积的预测值。将获得的预测值与测量值对比分析，并计算二者的决定系数R2和均方根误差(Root mean squared error，RMSE)。

表1为PLSR算法获得不同冠层的叶面积探测模型R2和RMSE。由测试集数据分析得出，稠密且厚度较大的冠层获得的叶面积探测模型拟合精度最大，数据的离散程度最低。稠密且厚度小的冠层获得叶面积探测模型的精度次之。冠层稀疏且厚的探测模型精度低于稠密冠层，但高于稀疏薄冠层的探测模型。

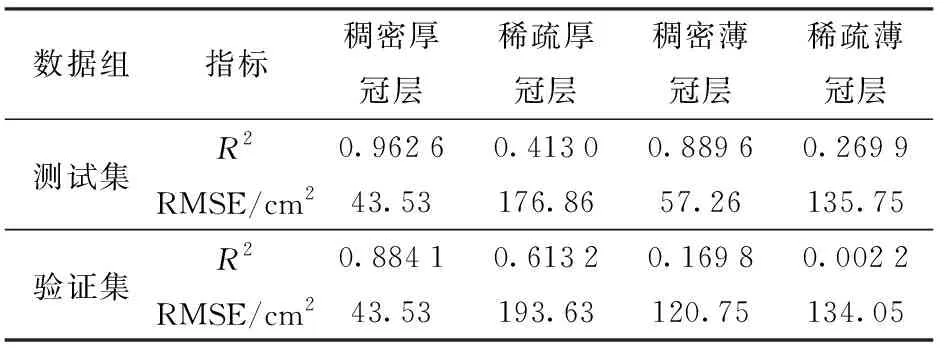
表1 基于PLSR算法的R2和RMSETab.1 R2 and RMSE values based on PLSR algorithm

验证集数据组验证结果得出叶面积探测模型对稠密厚冠层拟合效果较好，稠密薄冠层次之，稀疏薄冠层最差。数据的集中程度(RMSE表示)由大到小依次为稠密厚冠层叶面积、稠密薄冠层叶面积、稀疏薄冠层叶面积和稀疏厚冠层叶面积。稀疏薄冠层RMSE小于稀疏厚冠层。这与测试集中稀疏薄冠层的叶面积关系方程精度最小，但数据离散程度不是最高，数据对比结果一致。造成这种现象的原因为：①随机提取验证集过程中，数据提取较为分散。②稀疏薄冠层点云数据较稀疏厚冠层点云数据集中。

2.3 基于BP神经网络算法的冠层叶面积探测模型

采用BP神经网络研究树形靶标冠层厚度和LiDAR点云数与冠层叶面积的关系模型，模型建立的过程中同样设置测试集和验证集，比例为7∶3。BP神经网络设置为2个输入(LiDAR点云数和冠层厚度)和单个输出(冠层叶面积)模式。设置隐藏层节点数为3，网络学习率为0.01。设置当均方根误差小于0.01 cm2时，训练结束。BP神经网络对稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层4种仿真冠层进行叶面积探测模型研究，对模型进行多次训练。对比真实值和预测值，获得模型对冠层叶面积计算的能力。

图10为通过BP神经网络叶面积探测模型获得的稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层的预测值与真实值之间拟合图。获得的BP神经网络冠层叶面积探测模型的R2分别为：0.972 7、0.530 2、0.899 3、0.429 0。图中函数方程为真实值(T)与预测值(Y)之间的关系。T1～T4和Y1～Y4依次为稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层叶面积的真实值和预测值。由预测值与真实值的关系方程的斜率和截距，得出稠密厚冠层斜率接近1，截距最小，获得的叶面积关系模型拟合效果最好，其次为稠密薄冠层、稀疏厚冠层和稀疏薄冠层。

采用验证集对获得的BP神经网络回归关系模型进行验证，获得预测值，对比其与真实值之间的相关度如图11所示。由图11分析得出，预测值与真实值之间决定系数分别为：0.934 7、0.472 0、0.646 3、0.285 3，稠密冠层中预测值与真实值的拟合效果优于稀疏冠层的拟合效果。稠密厚冠层拟合效果最好，稠密薄冠层的拟合效果次之。该分析结果与PLSR算法获得叶面积探测模型结果一致。通过模型预测得出稠密冠层的预测精度可用于预测仿真冠层的叶面积。对于稀疏冠层，经过BP神经网络运算，模型的精度得到提高，与测试集结果一致。但由于模型的精度仍然较低，验证集预测值的R2小于0.5，对稀疏冠层叶面积预测准确率较低，需要进一步对稀疏冠层叶面积关系模型进行试验，采用不同的数据处理方法和计算算法研究稀疏冠层叶面积探测模型。

3 讨论

本文在经典回归算法的基础上，采用具有明显回归优势的PLSR算法和BP神经网络算法研究冠层叶面积探测模型。

对比PLSR算法，通过R2差值对比相同稠密度的冠层厚度的影响，冠层稠密情况下，冠层厚度对叶面积关系模型的影响较小(0.073)；冠层稀疏情况下，叶面积探测模型的拟合度较小，冠层厚度对叶面积计算影响较大(0.143 1)。由于稠密冠层截获激光束能力较强，激光束不能穿透稠密冠层树叶，厚度对稠密冠层叶面积探测模型影响较小；稀疏冠层对激光束截获能力弱，激光束能够通过冠层孔隙穿透冠层，被不同冠层厚度处叶片截获，冠层厚度对稀疏冠层叶面积探测模型计算影响较大。对比BP神经网络获得的叶面积探测模型的R2，判断得出稠密冠层获得的叶面积探测模型精度高于稀疏冠层叶面积探测模型，厚度大的冠层拟合精度大于厚度小的冠层。由不同冠层情况下R2之间的差值，得出稠密度对叶面积关系模型影响较为显著，冠层厚度对叶面积关系模型的影响较小。通过BP神经网络分析获得结论与PLSR算法分析结果一致。

通过模型拟合精度的R2，得出BP神经网络算法获得的叶面积探测模型精度高于PLSR算法获得探测模型，稠密厚冠层、稀疏厚冠层、稠密薄冠层和稀疏薄冠层精度分别提高了0.017 1、0.117 2、0.009 7、0.159 1。BP神经网络算法对稠密厚冠层叶面积探测模型精度提高较少(最大0.017 1)，对稀疏冠层提高较多(最大0.159 1)，说明2种算法对稠密冠层的叶面积探测模型拟合精度均较高，而对于稀疏冠层叶面积探测模型拟合精度差距较大，说明BP神经网络能明显提高稀疏冠层叶面积探测模型的拟合精度。综合分析得出BP神经网络算法能够不同程度地提高模型精度，对不同冠层情况具有较强的适应性，优于PLSR算法。

文献[22-23]获得冠层叶面积与LiDAR点云数据的拟合模型精度较好，由于二者研究的室内仿真树冠层树叶较为稠密，树叶间孔隙小，能够较好截获LiDAR点云数据。文献[22]同时针对矮化墙式果园进行叶面积与LiDAR点云数据关系研究，由于研究对象为墙式果树，树叶在树干上分布较为稠密集中，且冠层较薄，获取二者的拟合精度较好。本文针对稠密厚冠层和稠密薄冠层进行了研究，获得的叶面积探测模型拟合精度较高。上述研究与本文对稠密冠层叶面积探测模型的研究结果类似，均表明稠密冠层获得的叶面积探测模型较好。相比前人研究的稠密冠层，稀疏冠层叶面积探测模型也在本文展开研究，获得了稀疏冠层的叶面积探测模型。经过计算得出探测模型的拟合精度较低，介于0.269 9～0.530 2之间，但模型建立为后继研究提供了参考依据。为了获得更好的稀疏冠层叶面积探测模型，在现有研究基础上，优化数据处理方法，深入研究探测模型的拟合算法，以期为稀疏冠层叶面积计算提供更优的探测模型，为精准变量喷药的药量计算提供依据。

本文研究了冠层叶面积与LiDAR点云数据和冠层厚度探测模型，增加冠层厚度为影响因素，将叶面积计算由二维空间转为三维立体空间中，更符合果树冠层内树叶分布的实际情况。对比文献[22-24]的研究结果，厚度对叶面积探测有重要影响不能忽略。本研究获得的叶面积探测模型有望获得较好的实际应用效果。

4 结论

(1)搭建了树形靶标三维立体测量试验平台，对冠层不同区域在立体空间位置进行了定位，实现冠层区域内叶面积三维立体化测量。

(2)通过PLSR算法和BP神经网络算法计算获得冠层叶面积探测模型，得出稠密冠层探测模型拟合精度较高，稀疏冠层探测模型拟合精度较差；BP神经网络算法能显著提高模型的精度，精度最多可提高0.159 1。

(3)对比PLSR算法和BP神经网络算法，得出BP神经网络算法获得的叶面积探测模型精度更高，BP神经网络算法优于PLSR算法，对不同冠层的适应性更强。

(4)提出基于三维立体空间树形靶标冠层叶面积探测模型，可用于较稠密冠层叶面积在线计算，指导果园精准变量喷药。研究中获得模型对稀疏冠层叶面积探测模型的精度较低，后期需要针对稀疏冠层叶面积探测模型进行深入研究。