一类季节交替下具有一般功能反应的捕食-食饵模型的动力学分析
杭 磊,张 龙,王晓雯
(新疆大学 数学与系统科学学院,乌鲁木齐830046)
1 引言和预备知识
自然环境的季节交替对生物种群具有极大影响,季节性变化的环境将影响种群的增长[1-2]、种间关系[3-5]、传染病动力学行为[6-7]和群落结构[8-11]等.相关学者对具有季节交替的生物种群的动力学行为进行了广泛研究[1,3-7].文献[1]和文献[3]将一年分为“好的季节”和“坏的季节”.文献[1]建立了在季节演替和脉冲扰动下的单种群系统,在“好的季节”种群增长较快,在“坏的季节”种群增长较慢,甚至负增长,得到了正周期解的存在唯一性和全局稳定性.文献[3]考虑具有季节演替的非自治Lotka-Volterra 竞争模型,在“好的季节”两种群互相竞争,在“坏的季节”两种群无竞争,研究了平衡点和周期解的稳定性.文献[6]研究了一类季节性的SIR 流行病模型.
考虑到种群的增长方式与种间关系是随季节变化的,文献[5]建立了基于负增长与Logistic 增长交替进行的两种群竞争模型

其中:m∈N;λi、ri和Ki分别为种群xi的自然死亡率、内禀增长率和环境容纳量;α 和β 分别为种群x1和x2的竞争系数.模型由周期性交替的2个连续季节(S1,S2)组成:在S1(坏的季节)中,即t∈[mω,mω+(1-φ)ω]时,两种群无竞争;在S2(好的季节)中,即t∈[mω+(1-φ)ω,(m+1)ω]时,两种群互相竞争.
在现实世界中,种群间不仅存在竞争,还有捕食以及合作关系,因此本文考虑如下基于Gompertz 与Logistic 交替增长的捕食-食饵模型

其中:k∈N;x为食饵种群,y为捕食者种群;正数ri、ki、ai和bi(i=1、2)分别为食饵的内禀增长率、食饵的环境容纳量、捕食者的内禀增长率和捕食者的死亡率,正数c1为捕食者的营养转化率;功能反应函数φ(x)为捕食率,即每个捕食者捕获的食饵数量.模型由2个连续季节(S1,S2)组成:在S1 中,即t∈[2kω,(2k+1)ω]时,捕食者捕食食饵;在S2 中,即t∈[(2k+1)ω,(2k+2)ω]时,捕食者不捕食食饵但有其他食物来源.
本文对模型(2)做如下假设:
(A1)当食饵种群密度增大时,每个捕食者捕获的食饵数量随之增大,即捕食率函数φ(x)增大[12].因此假设φ(x)在[0,+∞)上单调递增,且关于x可微,φ(0)=0.
考虑单种群模型
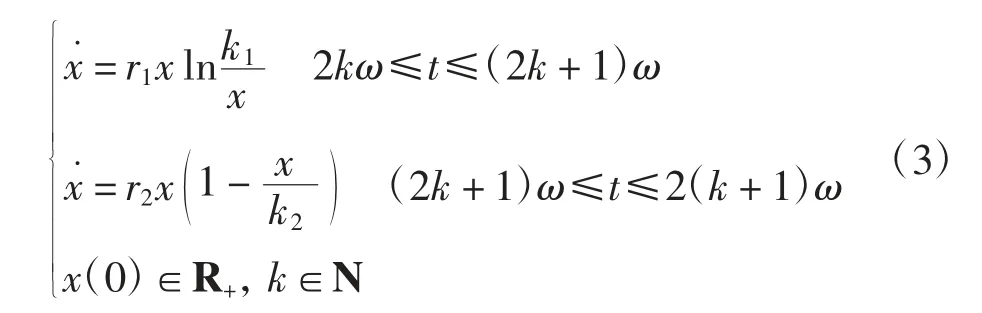
为方便,将模型(3)改写为


对模型(4)和(5)做如下假设:

引理1[1]若假设(A2)成立,则模型(4)(或(5))有唯一全局渐近稳定的正周期解u0*(t).
对于纯量微分方程

有以下结论.
引理2[13]设(ft,x)和F(t,x)在平面G上连续,且满足f(t,x)≤F(t,x),(τ,ξ)∈G.若x=φ(t)和x=Φ(t)分别为方程(6)和(7)定义在a <t <b上的唯一解,则有φ(t)≤Φ(t),τ≤t <b.
容易看出,模型(2)任意具有正初始条件(x(0),y(0))的解(x(t),y(t))在(0,+∞)内恒正.
2 主要结果
2.1 有界性
定理1设(A1)和(A2)成立,则存在常数M>0,使得模型(2)的任意正解(x(t),y(t))满足

证明令(x(t),y(t))为模型(2)的任意正解. 当t≥0 时,有

考虑如下辅助方程

由引理2 可得x(t)≤u(t),t≥0,其中u(t)为方程(10)的解,且u(0)=x(0).由引理1 知,方程(10)存在唯一全局渐近稳定的正周期解因此,对于任意常数β1>0,存在常数T1>0,使得

故有

所以,由模型(2)及(A1)可得

由引理2 可得y(t)≤v(t),v(t)为下列辅助方程的解,且v(0)=y(0).

其中:


所以

令M=max{M1,M2},则有

证毕.
由(A1)及Lagrange 中值定理[14]可得,存在ξ1∈(0,x(t)),使得

考虑模型


对于模型(17),进一步做如下假设:

推论设(A3)成立,则模型(16)存在唯一全局渐近稳定的正周期解且其中为模型(4)的唯一周期解.
证明由引理1 知,模型(16)存在唯一正周期解由于方程(17)右端关于z(t)满足局部Lipschitz条件,根据常微分方程解对参数的连续依赖性[13],可知方程(17)的任意解z(t,t0,z0,ξ)(z0= x0)关于(t0,z0,ξ)是连续的.进而可得模型(16)的唯一正周期解关于参数ξ 连续.因此有证毕.
2.2 持久性
定理2设(A1)~(A3)成立,a1≥a2,且

则模型(2)是持久的,即存在常数M >m >0,使得模型(2)的任意正解(x(t),y(t))满足

证明由定理1,只需证明存在常数m >0,使得对于模型(2)的任意正解(x(t),y(t)),存在常数当时,有x(t)≥m,y(t)≥m.
先证明x(t)持久.设(x(t),y(t))为模型(2)的任意正解,由定理1,存在常数T2>T1,使得

当t≥T2时, 由Lagrange 中值定理知, 存在常数ξ1∈(0,x(t)),使得

由模型(2),当t≥T2时,有
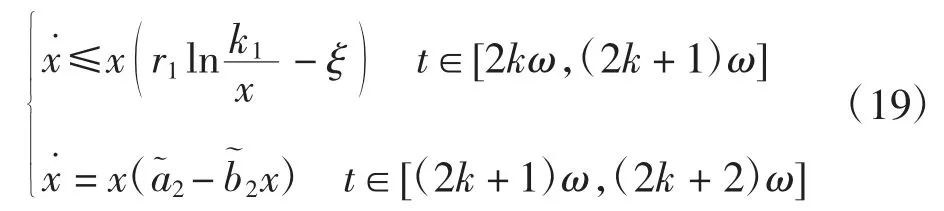

x(t)持久性得证.
下面证明y(t)持久.由条件(18),可选取充分小的常数ε0>0,使得

由推论知

因此,对于上述常数ε0,存在常数ξ0>0,使得


其中u(t)为模型(16)中当ξ=ξ0时的正解,且u(t0)=u0.进一步得

选取充分小的ε1,ε1≤ε0.考虑y(t),y(t)存在下列3种情况:
情况1存在常数使得y(t)≤ε1,t≥T*.
情况2存在常数使得y(t)≥ε1,t≥T*.
情况3存在区间列{[sn,tn]},满足T2≤s1<t1<s2<t2<…<sn<tn<…,且使得当tn]时,y(t)≤ε1,y(sn)=y(tn)=ε1,当时,y(t)≥ε1.



对于任意整数k≥0,取t∈[T3+2kω,T3+(2k+1)ω],其中对不等式(28)由T3到t 积分可得

再考虑情况3.对于任意t≥T2,当时,对于某个正整数n,有t∈[sn,tn].

则对任意t∈[sn,tn],有


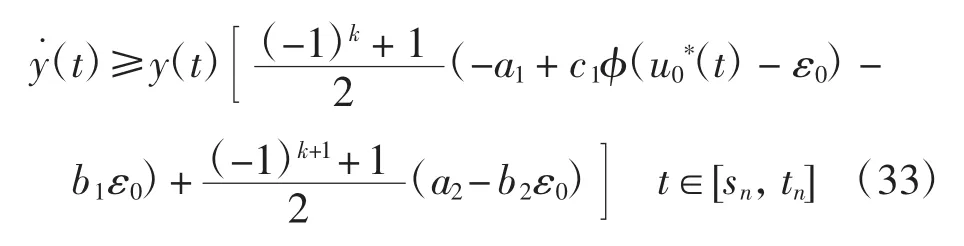

最后考虑情况2.由y(t)≥ε1,t≥T*可得

综上,对于模型(2)的任意正解y(t),由式(34)~式(35)可得持久性得证.证毕.
3 数值模拟
在模型(2)中,令r1=0.5,r2=0.25,k1=10,k2=5,a1=0.6,a2=0.5,b1=0.1,b2=0.1,φ(s)=显然,a1=0.6 >a2=0.5.计算得


因此,由定理2 知模型(2)是持久的.取3 组初始条件为(x(0),y(0))=(2.5,5.5)、(1.5,6.5)、(3.5,7.5).图2给出了模型(2)中x(t)和y(t)的图像.

图1 单种群的周期解图像Fig.1 Image of periodic solution for the single population

图2 模型(2)中x(t)和y(t)的图像Fig.2 Images of x(t)and y(t)for Model(2)
4 结语
本文研究了具有一般功能反应的季节交替的捕食-食饵系统,得到了系统的有界性和持久性等结果.在生态环境治理过程中,可利用系统有界性和持久性条件制定相应措施,以保证生物资源的可持续再生,达到保护生态系统多样性的目的.

