高职一元函数微积分概念的教学策略研究

(湖北交通职业技术学院，湖北武汉 430079)

1 数学概念的意义

数学概念是现实世界的空间形式和数量关系及其本质属性在思维中的反映，具有抽象性和具体性双重特点。学习数学离不开数学概念，数学基本概念是形成学生数学能力的基础，数学内容的全部展开，都立于数学概念之上，概念理解正确与否，直接影响到数学公式、法则、定理的学习。数学概念是数学学习的核心，不仅要记住它的定义，认清它代表的符号，更重要的是要真正把握它的本质、属性[1]。高职学生数学教学在提高学生素质与数学能力的同时，还应提高学生的应用能力，即用数学解决生活或专业问题的能力，而数学概念的理解与应用对提高学生的这一能力尤为重要，在解决数学问题时，学生出错或产生困难的主要原因往往在于不理解概念，特别是对同一数学概念的不同表达形式，概念之间的相互关系等缺乏系统概括的理解，因此高职数学教学必须十分重视概念教学。

2 高职学生概念学习中的问题

数学概念是高职数学教学的重点和难点。由于高职学生的学习能力与对数学学习的认识欠缺，在数学概念学习中存在许多问题[2]：

(1)不重视数学概念，认为学好数学主要是学会用公式、定理等算题，做题时往往忽视概念。

(2)对数学概念倒背如流，但不懂其含义。如函数的概念，很多学生能很熟练地背出来，但若要例举生活中的函数关系或建立实际问题中的函数关系，往往不知所措。

(3)对数学概念片面理解。如函数在某点处连续的概念，认为只要函数在某点处极限存在或有意义就一定连续，而事实上函数在某点处连续要同时具备三个条件(在某点处有意义、有极限、极限等于函数值)。

(4)不会应用概念解释实际问题。如导数(函数增量与自变量增量的比值当自变量增量无限趋于零时的极限)概念的使用。

(6)不明白概念所体现的数学思想和方法。如定积分概念所体现的逼近思想、以直代曲、以不变代变的方法和极限的方法等。

(7)受已有知识的理解或影响而对概念产生误解。如曲线的切线的概念，很多学生受圆的切线的概念影响，认为曲线的切线就是与曲线只有一个交点的直线，事实上是曲线在切点处的割线的极限位置，是曲线的局部特征。

3 高职学生一元函数微积分概念教学的几种策略

3.1 提高学生对数学概念的认识

3.1.1通过实例引入概念

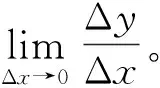
3.1.2介绍数学概念与法则、公式、性质等之间的关系

很多学生在学习数学时，认为概念的意义不大，只要是会用性质、法则或定理等做数学题。如求函数的导数，一般会用到求导公式、法则等，尤其是高职学生，很少会用导数的概念求导数。所以高职学生对导数的概念只是停留在“函数增量与自变量增量的比值当自变量增量趋于零时的极限”这句话上面，很少会主动去理解导数概念的意义。而事实上导数的公式、法则等并不是脱离其概念而存在的，而是由其概念推广、引申出来的或是深层次的表述，所有的公式或法则都可以通过定义证明或理解。再比如函数的极限、微分、积分公式与法则或性质也都可以由其概念进行理解与证明。在数学教学中，我们不只是要教学生会做题，更主要的是应该教学生会学、会用，而数学方法有很多，但是万变不离“概念”。

3.2 引导学生理解概念，提高分析能力和应用能力

3.2.1引导学生用数学语言描述抽象的文字性概念

学生数学语言能力直接影响数学学习，在数学的学习中，很多学生对数学符号、等式与文字之间的关系不能对应起来，所以平时的教学中，尤其要注重数学符号与文字或描述性语言之间的对应关系。如函数极限的描述性定义为：当自变量无限增大(或无限接近于某一固定点)时，函数的值无限接近于一个确定的常数，则该常数就是函数当自变量趋于无穷(或固定点)时的极限。我们可结合利用图形，引导学生通过表1进行对比，解释该概念的数学符号表示，同时强调A、δ、N、ε的意义。然后通过实例进行讲解，让学生理解描述性语言与数学语言之间的对应，促进学生对概念的理解，培养学生的数学能力。

表1 概论的数学符号表示

3.2.2引导学生剖析概念所涉及的数学方法与思想

掌握数学概念，最主要的是会用数学概念解决实际问题，以及用到了什么方法或数学思想。比如定积分的概念，我们一般是通过曲边梯形的面积和已知变速直线运动的速度求路程两个问题而引入的，在教学中我们可引导学生首先分析曲边梯形的面积和已知变速直线运动的速度求路程这两个问题的共同特点是“不规则性(非稳恒性)”与“可加性”，然后启发学生解决这一类问题常用的数学方法是先切割，再“化不规则为规则” 或“化变为不变”(即利用近似的方法)，最后求和、利用无限逼近的思想(即极限思想)。这样不仅能培养学生分析问题的能力还能让学生形成良好的分析问题的习惯，结合实际问题的特点归纳并梳理自己平时所学的数学内容与方法，从而理解概念所涉及的数学方法与思想，提高学生的分析能力与应用能力，这还有助于学生进一步理解与之相关的概念或数学方法。

3.2.3引导学生将具体问题转化成概念中的具体因素

在数学概念的教学中，许多学生理解概念，也理解概念解决的问题领域，但是如何用概念或数学表达式表示问题、解决问题通常无从下手。主要原因是找不出问题中的变量以及变量间的关系。如导数的概念，许多同学知道与变化率相关的问题可用导数的概念，当对于高职学生来说，如何判断一个问题是否为变化率的问题，问题中谁是函数，谁是自变量等都有一定的难度。那么在教学中，我们就要引导学生分析要求的量与哪些因素有关，在物理学或其他领域是如何定义的，如已知路程求变速直线运动的瞬时速度，我们知道速度是路程对时间的变化率，即要求的量“速度”与两个因素有关，“时间”和“路程”，而路程与时间的关系是已知的，即该问题中路程是已知函数，时间为自变量，所以直线运动的瞬时速度就是路程(函数)对时间(自变量)的导数(可参考通过实例引入概念，提高学生对数学概念的认识)，再比如交流电路中已知电量与时间的关系求电流(单位时间内通过的电量)，即电量对时间的变化率，所以电量对时间的导数就为电流。

3.3 理清概念间的关系，提高学生的思维能力

3.3.1掌握极限是微积分的基础

我们知道，极限的概念因抽象而不好理解，所以在教学中，我们一方面可以结合图像、对比表一、通过应用加强高职学生对极限概念的理解，另一方面微积分的大部分概念都是通过极限定义的，如无穷小量、连续、导数、定积分、反常积分等，所以我们可以通过这些概念的讲解进一步帮助学生巩固对极限概念的理解。

3.3.2区分概念间的相互关系

在一元函数微积分的教学中，有的概念与某量有关系，如一元函数的连续、可导、可微的概念中都用到了函数的增量，即当自变量增量趋于零时，若函数在某点处的增量的极限为零，则函数在该点处连续；若函数增量与自变量增量比值的极限存在，则函数在该点处可导；若函数增量可表示成自变量增量的一个线性函数与一个自变量的较高阶无穷小(当自变量增量趋于零时)的和，则函数在该点处可微。由这三个概念，我们可得出函数在某点可导必可微，可微必可导，可导必连续，但连续不一定可导；而且导数是增量比值的极限，而微分是自变量增量的线性函数(主要部分)。有的概念是“个别”与“全体”的关系[4]，比如原函数与不定积分，原函数指的是一个函数，而不定积分指的是原函数族(即所有原函数)。还有的概念从计算方面有联系，比如不定积分与定积分，定积分是一个和式的极限，定积分用牛顿莱布尼兹公式计算时与被积函数的原函数有关，而原函数可以通过不定积分求出来。有的概念看似是另一概念的推广，而且解决的问题也类似，但定义不同，比如定积分与反常积分，实际上反常积分是一个函数(变上限或变下限函数)的极限。

4 结 语

总之，在高职数学教学中，要根据学生概念学习情况，有针对性地选择教学策略，注重引导，加强应用，让学生理解概念、用好概念，为学生后续相关专业课程的学习奠定坚实的基础。