选择最佳新思路 多想少算不是梦——以2020年南通一模第12题为例

江苏省平潮高级中学(226361) 周 炎

2020年南通一模考试填空题第12 题是一道条件清晰简明的三角形中的最值问题,难度系数0.75,然而统计填空题的答题时间时,发现在这道题上大部分同学花费了较长时间,直接影响了整张试卷的得分.对于这种中档小题,会做却需要花费较长时间,笔者深感“多想少算”这一思想的重要,现试从多种角度进行剖析,以促进学生学会思考、帮助学生寻找最佳新思路,进而发展学生的数学思维能力.

一、题目及命题意图

题目已知∆ABC的面积为3,且AB=AC.若则BD的最小值为____.

命题意图此题本意是要考查基本不等式求最值.命题人给它设置了三角及向量背景,将高中数学三个重要考点综合起来,提升了区分度.

二、解法剖析

思路1(理解运算背景,设计解题思路,重函数思想)本题研究的是三角形中的边长的最值问题,对于这样的问题,可画出三角形,结合正弦定理的面积公式及余弦定理可建立等量关系,并构造目标函数,研究最值.

解法1设AB=AC=m,则

在∆ABD中,由余弦定理有

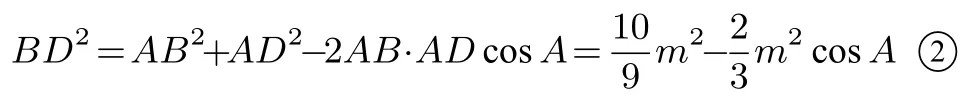
点评解决最值问题的常规方法,过程较繁琐,运算量较大,需要较强的运算能力及耐心,不符合小题小做、多想少算的原则.

思路2(理解运算情境,设计解题思路,重解析思想)本题研究的是一个等腰三角形中的问题,对于这样一个相对特殊的几何图形,我们要思考如何能够更便捷的表示面积及BD边长,显然利用两点间距离公式等解析几何知识较为方便.那么我们不妨选择解析法,建立直角坐标系,找等量关系,研究最值.

解法2如图1,以BC所在直线为x轴,垂直平分线为y轴,建立如图所示直角坐标系.

设B(−m,0),C(m,0),A(0,h),其中m >0,h >0,则所以当且仅当即时,

图1

条件AB=AC及的另一层含义就是AB= 3AD,此时我们是否种熟悉的感觉呢?正所谓此时无圆却有圆,找准入口现“圆”形,“圆”来她就在这里.

解法2′以BD所在直线为x轴,其垂直平分线为y轴,建立如图2示直角坐标系.

设B(−m,0),D(m,0)(m >0),A(x,y),由AB=3AD,有(x+m)2+y2= 9[(x −m)2+y2].化简可得点A的轨迹方程是

图2

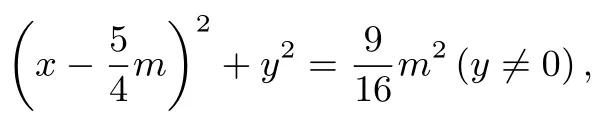
结合题意可知∆ABC的面积是∆ABD面积的3 倍,所以∆ABD的面积为1,从而

点评以上两种解法本质上都是采用解析的思想,它是高中数学的重要思想方法之一,不仅仅体现在解析几何中,在三角、向量问题中若能恰当的选择解析法,能够较大程度的优化解题过程、减小运算量.当然,在本题情境下前一种做法运算量较小,但我们绝不能忽视后一种方法,它实质上是抓住了隐含在问题中的特定运算情境——阿氏圆.

思路3(挖掘运算方式,设计解题思路,重向量工具性)本题中不仅是三角形背景,还增加了平面向量的元素.我们知道,平面向量不仅是高中数学重要考点,同时还是数学中的又一重要工具,那么能否从向量的角度来研究BD的长度呢?我们结合三角形面积这一已知条件,不妨从选择基底开始,寻找思路切口.

解法3∆ABC为等腰三角形,故取BC中点E,连接AE,且BC ·AE= 6.因此选择以为基底,则

图3

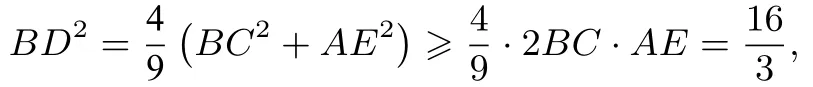
点评把线段的长理解成向量的模,根据平面向量基本定理,平面内任一向量可用该平面内两个不共线的向量表示,条件中等腰三角形面积为定值的特点是解决问题的重要抓手,据此选择基底,能较快的表示所求量.这样的处理,运算量减少了,但需要对问题有较为深入的思考.

思路4(挖掘背景内涵,设计解题思路,回归几何本质)本题更是一道平面几何题,能否回归几何本质,结合图形特征,借助平几方法求解呢?那么我们不妨从构造辅助线开始.

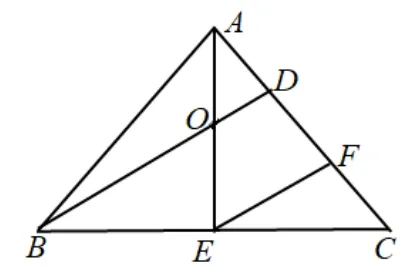
图4

解法4取BC中点E,连接AE,设BD与AE交于点O,取CD中点为F.由平几知识可知,为AE中点,所以,BO2=BE2+OE2,而BE ·则BO2=BE2+OE2≥2·BE·OE=3,当且仅当BE=OE=时,

点评深度挖掘问题内涵,充分利用图形几何特征,适当构造辅助线,达到了优化解题思路的目的.以思助算,大幅减少运算量,提高了解题速度及正确率.

我们还可以结合雷达图对以上四种解法从知识面、思维量、计算量、能力等方面进行比较:

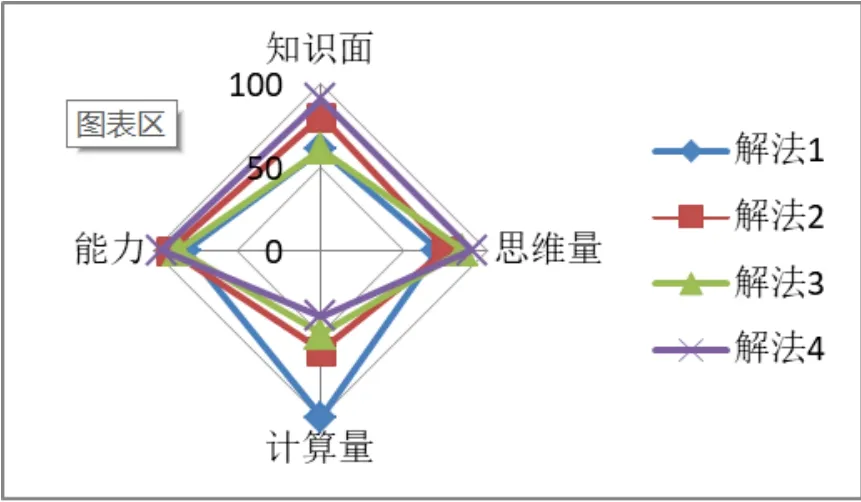
不难看出,从计算量的角度来衡量我们应当选择解法4,但它对学生的知识面及思维能力要求高,特别是对初中平面几何知识的掌握;解法2 的运算量略大一些,但属于高中阶段重要的也是常见的方法,运用解析法解决与平面图形有关的问题往往能产生意想不到的效果;解法3 则需要很强的思维能力,特别是在基底的选择上,选择不恰当有可能适得其反;而解法1 对计算能力及思维能力均有较高要求,对于这样一道填空题来说,显然不是一个好的选择.

三、教学反思

(一)明析问题背景,做多向之想

多向之想是在明析题目背景的基础上对问题进行代数及几何角度的思考.对于具体数学问题,我们要结合已知条件,深刻理解运算背景,寻求解题思路.案例中的运算背景为三角形,运算对象为三角形中的线段长,我们可以从解三角形的角度去研究,形成解法1;我们也可以抓住等腰这一特殊性及等分点,借助平面几何知识去研究,形成解法4.对于数和形的不同角度,产生差异明显的数学运算.在这个过程中,“多想”是关键,找到更为合适的方向切入,进而提升解题速度,体现了变向求解的解题智慧.

(二)理解运算方式,做多面之想

高中数学中的运算有实数运算,也有向量运算.在不同的情境中,不同运算方式在解决问题时所产生的的运算量会有较大的差异.恰当的将两种运算相融合,会有意想不到的效果.案例中还含有向量形式,我们可以尝试选择合适的基底表示,进而研究的模,形成解法3.这样的处理,源于对问题的深入思考,更源于对运算方式进行了多面之想,达到了“以想破算”的目地,体现了运算手段的灵活性.

(三)深挖情境内涵,做多次之想

对运算情境内涵的深刻挖掘,促使我们综合的运用所学数学知识、思想方法将问题迁移到不同情境中去.高中阶段学习了解析几何,其本质是用坐标法研究几何问题,而案例呈现出的就是一个几何模型,由此形成解法2.1.再次解读题意,剖析图形特征,形成解法2.2.诚然解法2.2 在此题中并未展现出优越性,但这样的思考无疑对其它类题的求解提供了极好的思路.对同一类型方法做多次之想,它不仅仅是解了一道题,更促进数学思维的发展.

在解题教学中,我们应指导学生从问题背景、运算方式、情境内涵等不同角度进行全方位的思考,并进一步厘清不同解法运算的烦简程度.以思助算,用思简算,算思结合,方能高效解题.