由两道模考试题引出椭圆的一个充要条件

湖北省松滋市第一中学(434200) 王 波

题1(2020年福州市高三元月调考试题)已知圆椭圆的短轴长等于圆O半径的倍,C的离心率为

(1)求C的方程;

(2)若直线l与C交于A,B两点,且与圆O相切,证明:∆AOB为直角三角形.

题2(2020 届合肥市高三第一次教学质量检测)设椭圆的左右顶点为A1,A2,上下顶点为B1,B2,菱形A1B1A2B2的内切圆C′的半径为椭圆的离心率为

(1)求椭圆C的方程;

(2)设M,N是椭圆上关于原点对称的两点,椭圆上一点P满足|PM|=|PN|,试判断直线PM,PN与圆C′的位置关系,并证明你的结论.

两道试题都考查了椭圆的标准方程、直线与圆的位置关系、直线与椭圆的位置关系,考查了直观想象、数学运算、逻辑推理等核心素养,检验了学生分析问题与解决问题的能力.笔者在研究发现两道试题的第二问有相似之处,均涉及过椭圆直线与椭圆内一给定圆的相关问题,经过探索得到如下结果.

定理已知直线l与椭圆相交于A,B两点,则直线l与圆相切的充要条件是OA⊥OB.

证明(1)充分性

设A(x1,y1),B(x2,y2),①当直线l斜率不存在时,x1=x2,y1=−y2令l的方程为:x=x1,由于OA⊥OB,故即x1x2+y1y2=x12−y12= 0,又解得故l的方程为:故l与圆相切.

②当直线l斜率存在时,设l的方程为:y=kx+m联立l与椭圆C消去y得:(a2k2+b2)x2+2a2kmx+a2m2−a2b2= 0.由韦达定理得由于OA⊥OB,所以

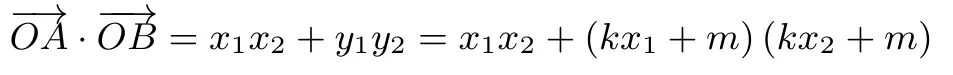
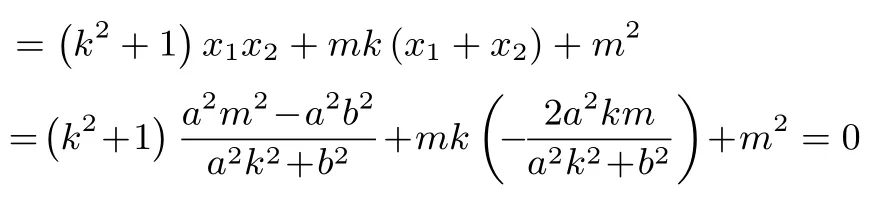
(2)必要性

①当直线l斜率不存在时,l与圆O相切,l的方程为:时,所以故OA⊥OB.当时,所以故OA⊥OB.

②当直线l斜率存在时,设A(x1,y1),B(x2,y2),l的方程为:y=kx+m,联立l与椭圆C消去y得:(a2k2+b2)x2+2a2kmx+a2m2−a2b2= 0.由韦达定理得

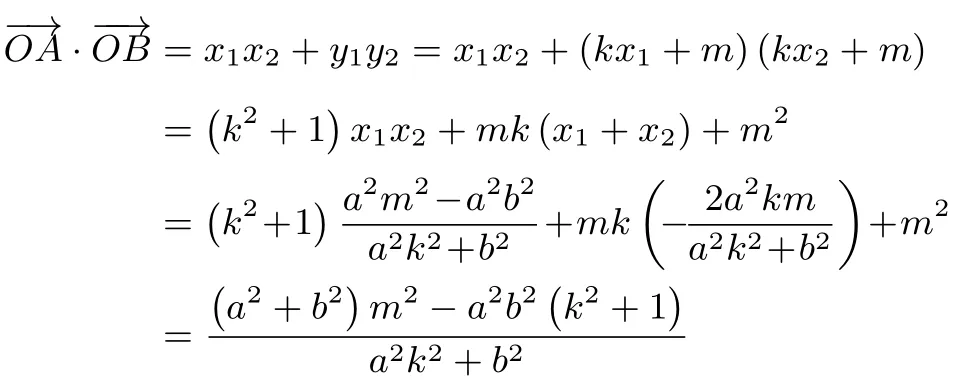
点O到直线l距离又l与 圆O:相切.所以即故

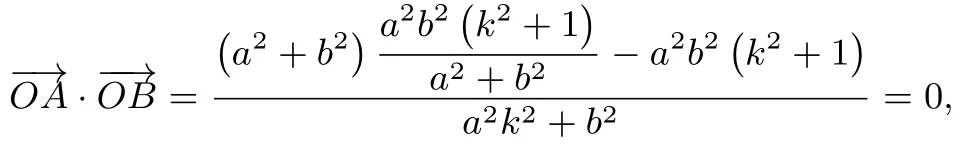
所以OA⊥OB.

评注题1 第二问实际上定理必要性特殊化考查,而题2 第二问是定理充分性特殊化考查,定理的证明过程即为两题第二问的解法.