高压油管压力控制的数学模型与优化

程 中 林

(安徽外国语学院 公共基础课教学部,安徽 合肥 231201)

0 引 言

近几年来，随着经济快速发展，中国对外贸易来往频繁，在交通以及各个方向对石油方面需求日渐增强。地球石油资源枯竭严重，因此高效利用石油资源十分重要。研究高压油管对于减轻目前的能源危机有一定的意义。

柱塞式柴油机在工作前，柱塞将柱塞腔内的燃油压缩，使得高压油泵内的压力大于高压油管内的压力。此时，单向阀打开，燃油通过单向阀进入高压油管内[1]。燃油进入油管后的波动会导致高压油管内产生引力波，引力波会使得油管内压力升高，如果不能合理控制单向阀的开关时间，可能会引起油管内的压力急剧变化产生事故。通过建立高压油管两端压力变化的方程，在固定单向阀打开时长的情况下，给出高压油管内压力和密度随时间变化的模型和算法，优化单向阀的开启策略。

采用2019年全国大学生数学建模竞赛A题中的数据，建立数学模型，解决高压油管在一定压力下单向阀的开启时长。

1 建模准备

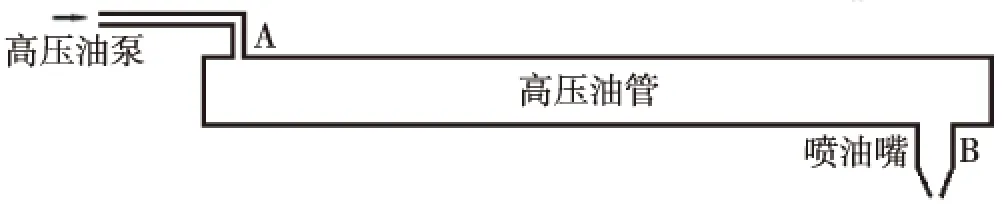
图1 高压油管简化工作原理

图1为高压油管简化工作示意图，给出某型号高压燃油系统的工作原理，燃油经高压油泵从A处进入高压油管，再由喷嘴B喷出[2]。燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化，使得所喷出的燃油量出现偏差，从而影响发动机的工作效率。

分析数据找出燃油在管中的不同过程，对不稳态过程利用流体力学中一维不稳定流动方程模型进行计算。燃油在高压油管中是非稳态，如果将油管划分计算单元，且高压油管一般比较细，可利用稳态方程进行求解。根据迭代法将高压油管内压力的波动性表示出来，结合一维不稳定流动方程建立偏微分方程。利用已知条件确定偏微分方程初始条件与边界条件，运用有限差值法解偏微分方程。根据具体问题，设置单向阀每次开启的时长，要保证高压管内压力在100 MPa左右，此时将问题进行理想化处理。假设高压管内压力稳定在100 MPa时，根据压力迭代方程，以进入油管和出去油管在1个极短的时间内进出油管的流体体积相等列出平衡方程式求得第1小问题的时间。在第2小问题相对于第1小问题增加了高压油管内压力增加的1个过程，然后在稳定后保持在150 MPa,此时将其分成2个阶段，先在2 s时间内将压力增加到150 MPa，根据非连续性压力增加过程按照积分公式求得在这段时间的单向阀开启时长，然后在稳定过程中根据第1小问的求解方法，求出第2个过程单向阀开启时间。其他时间段同理。

2 建立高压油管一维燃油流动稳态模型

对高压油管中的热传递过程进行分析，主要为流体稳定流动过程。

在稳定流动阶段，通过分析问题条件可以将问题合理简化为一维稳定流动模型[3]

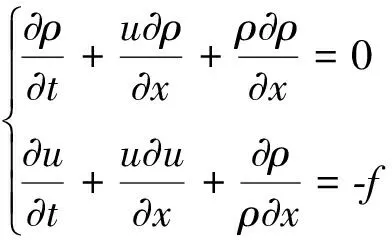
(1)

简化方程为

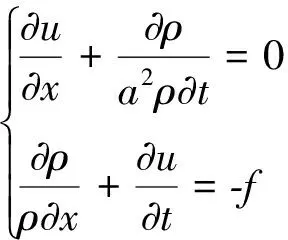
(2)

建立压力变化量与密度变化量的偏微分方程[4]

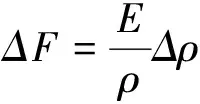
(3)

F=Elnρ+C

(4)

建立高压管压力迭代方程[3]

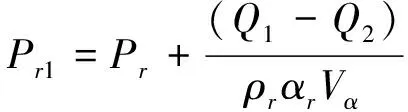
(5)

|Q1-Q2|≤ε1

(6)

建立高压油管压力增大流量模型[5]，进出高压油管的流量为

(7)

由(7)流量与压力的函数关系式推导出压力变化时高压油管压力增大积分模型

(8)

3 用MATLAB求解高压油管一维燃油稳态流动模型

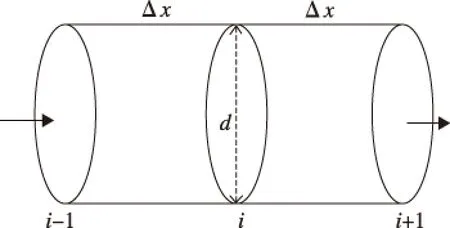
图2 高压油管划分

图2是高压油管划分示意图，将整个高压油管进行微元法处理，将高压油管微分为无数很小的一段，假如每一段上燃油的压强都能够稳定在100 MPa,那么整个高压油管内的压力就能够保持在问题要求的条件上。通过以上分析，建立并求解高压油管压力波动变化方程[6]。

油管里压力的初始条件为

P(x,0)=Pr

(9)

U(x,0)=0

(10)

其中，Pr为高压油管内残余压力。

若不考虑燃油在连接口处存在损失[7]，则

P(0,t)=Pr

(11)

P(L,t)=PN

(12)

根据压力的变化量与密度成正比的关系式，比例系数为E/ρ，其中密度保持不变，E为弹性模量[8]，和压力的关系式可用SPSS拟合得一阶和二阶的拟合曲线，其中二阶拟合曲线程度高达99.9%，由此可以得到弹性模量和压力的表达式[9]

E=1570+3.08F+0.03F2

(13)

图3是通过SPSS数据分析得到原曲线和一阶二阶拟合线，其中一阶拟合线拟合度为97.1%，二阶拟合线的拟合度为99.9%，所以选取二阶作为拟合曲线。

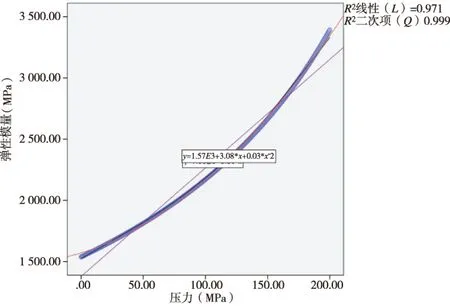
图3 弹性模量与压力的拟合曲线

由MATLAB可以做出凸轮的曲线规律图和针阀随时间运动曲线(图4～5)。

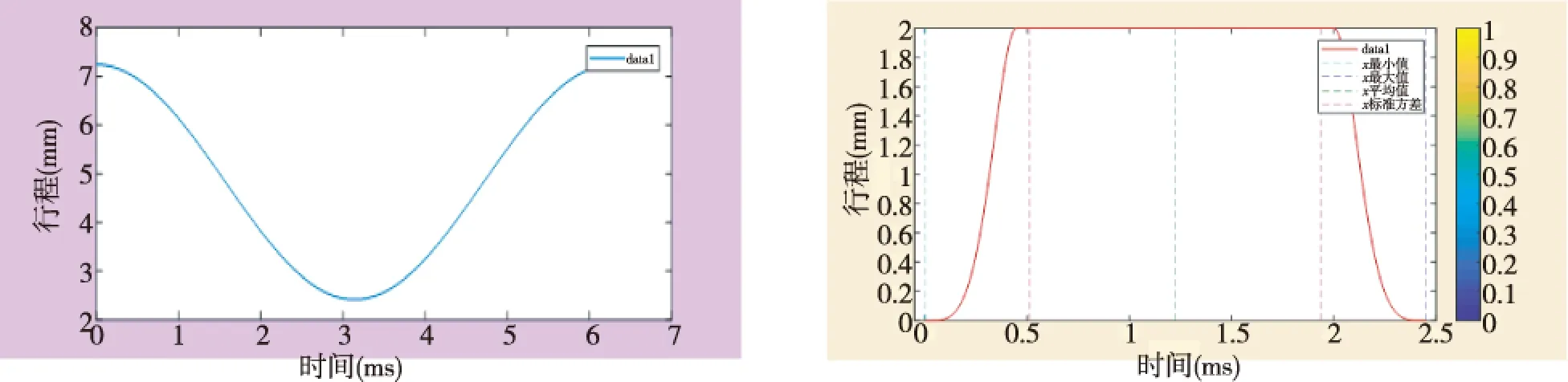
图4 凸轮运动规律 图5 针阀随时间运动曲线

根据计算，得到常数C为452.9，求得密度为0.9，再由C语言编写程序，对其公式利用MATLAB求解，得到单向阀每次开启的时长约为2.43211 ms。在2、5、10 s从100 MPa达到150 MPa单向阀所需时间分别为660.7、443.6、237.8 ms;达到150 MPa后，单向阀开启时间为10.674 ms能够让高压压管压力稳定在150 MPa。

4 模型优缺点

本文针对高压油管的压力控制，在一定压力下确定单向阀的开启时长。利用流体力学连续性方程建立高压油管一维燃油稳态流动模型，将高压油管压力变化用迭代法表示，在初始条件和边界条件下求解模型。利用MATLAB求出单向阀开启时长并拟合得到弹性模量与压力的方程，拟合度相当高，具有实际意义。不足的是忽略了燃油自身重力等一系列不确定因素，以及对实际柴油机高压油管复杂工作过程简化[10]，不具有普遍性。