一种基于距离测度的改进快速PCA人脸识别

陈 平

(徽商职业学院 电子信息系，安徽 合肥 230000)

人脸识别由于其在公安部门、安全验证系统、档案管理、信用卡验证和人机交互系统等方面的广阔应用，已经成为当前模式识别和人工智能的一个研究热点。人脸识别的主要方法有基于模板匹配的方法、基于面部几何特征的方法、基于子空间的分析方法、人工神经网络、支持向量机等。在众多的方法中，基于子空间主成分分析(principal component analysis，PCA)[1]是最经典的人脸识别方法之一。PCA又称为K-L变换，其实质是在尽可能好地代表原始数据的前提下，通过线性变换将高维空间中的样本数据投影到低维空间中。PCA计算中最主要的工作量是计算样本协方差矩阵的本征值和本征向量。其在人脸识别中计算的维度较大、计算的复杂度较高，通常会出现内存耗尽、计算时间长等问题。本文针对传统PCA计算过程慢、内存高的问题，使用了1种快速PCA的方法来进行人脸识别，在提高运算效率的同时加入了距离测度的考虑，提高了人脸识别率[2]。在著名的FERET人脸库中，基于距离测度的快速PCA方法能有效地进行人脸识别，且速度较快。

1 距离测度

最小距离分类又称为最近邻分类[3]，是一种非常简单的分类思想。这种基于距离的分类技术通过以一种原型模式向量代表每一个类别，识别时一个未知模式被赋予一个按照预先定义的相似性度量与其距离最近的类别。本文采用COS余弦距离、L1一阶范数、L2二阶范数来进行距离测度。对于2个向量x和y，其距离测度分别定义如下

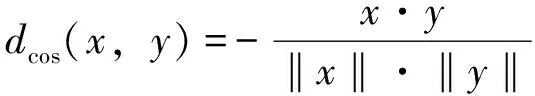
(1)

dL1(x,y)=‖x-y‖

(2)

dL2(x,y)=‖x-y‖2

(3)

2 快速PCA人脸识别算法

2.1 传统PCA人脸识别算法

对于1个二维的m*n像素的人脸图像通过行或列相连可以被转换成1个N=m*n的向量。通常这样的向量都是维数比较高的，识别起来比较困难。因此，在进行识别之前识别算法通常都会通过一些手段来进行降维。PCA正是将向量经过K-L变换后由高维向量转换为低维向量，并形成低维线性向量空间，即特征子空间，然后将人脸图像投影到低维空间，用所得到的投影系数作为识别的特征向量。识别人脸时，只需要将待识别样本的投影系数与数据库中目标样本集的投影系数进行比较，以确定与哪一类最近。

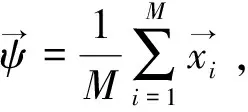
1)利用训练集图像计算特征脸

①将测试集中的M幅图像分别表示成列向量xi(i=1,2,…,M)，组成训练集矩阵T∈RN×M；

2)将人脸库中的图像投影到特征子空间[5]

将人脸库中的每张人脸向量减去均值之后投影到k个特征向量表示的特征子空间pcaEigVecsk，实现了人脸数据的降维表示。

3)使用距离测度进行人脸识别

将要测试的人脸图像投影到k个特征向量表示的特征子空间pcaEigVecsk,然后使用距离测度方法计算降维之后的人脸与数据库中存储的人脸图像之间的距离，依据最近邻原则进行识别，距离最近判断为最相似，同时可以设置最大人脸空间距离进行辅助判断。

2.2 改进的快速PCA人脸识别算法

在实验中发现传统PCA在进行人脸识别时，PCA算法对光照非常敏感[6],而且当样本的维数较大时，会出现内存耗尽、计算时间长、首次命中识别率不高等问题。因此本文针对实验中发现的问题提出了一种改进的快速PCA人脸识别算法。

1)针对光照敏感问题，对图像的灰度进行预处理，通过直方图均衡化来实现图像的灰度归一化，减少图像的亮度变化带来的影响[7]。

2)针对PCA计算样本协方差矩阵的本征值和本征向量内存高、时间长的问题，使用一种非常好的PCA计算技巧来计算[8]。具体过程如下。

设样本矩阵X大小为n*d(n个d维样本本征向量)，则样本协方差矩阵S将是一个d*d的方阵，协方差矩阵S=(YTY)d×d，因为d的维度一般较大，所以计算复杂度较高。现在考虑矩阵R=(YYT)n×n,一般情况下由于样本数目n远远小于样本维数d，R的尺寸也远远小于协方差矩阵S，可以证明其与S有着相同的非零本征值。证明过程如下。

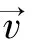
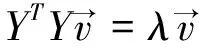
(4)

公式(4)两边同乘Y，并应用矩阵乘法的结合律得

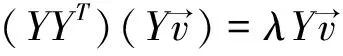
(5)

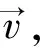
3)针对首次命中识别率不高的问题，本文提出根据本征向量重构测试样本特征向量与基于距离测度相似度排名靠前的人脸向量，再将重构的测试人脸图像与前80位重构的人脸图像进行比较，得到相似度最高的人脸[9]。人脸图像I的重构公式如下

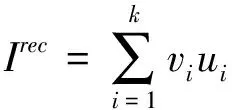
(6)

其中，Irec为重构人脸图像，vi为本征向量，k为本征向量维数，ui为人脸图像向特征脸空间投影所得到的投影系数。投影系数ui可以通过以下公式求出

(7)

3 FERET人脸库识别实例

FERET人脸库是由FERET项目创建，包含14 051幅多姿态、多光照的灰度人脸图像，是人脸识别领域应用最广泛的数据库之一[10]。本文在MATLAB 2013a中编写程序进行实验，实验样本取自FERET的1 208个人，其中每个人大约有11幅图像，每幅图像都是384*256像素。实验中使用2种标准方法来衡量实验结果[11]。

1)首次命中识别率，距离测度结果中排名第一即是正确的识别结果的概率。

2)累计匹配识别率(cumulative match score，CMS),本文累计前80位识别概率之和。

图1和图2是基于PCA的人脸识别CMS结果和改进的快速PCA的CMS结果。从图2中可以看到改进的快速PCA的首次命中识别率更高，CMS累计识别准确率提高。而且实验中快速PCA明显提高了计算速度。

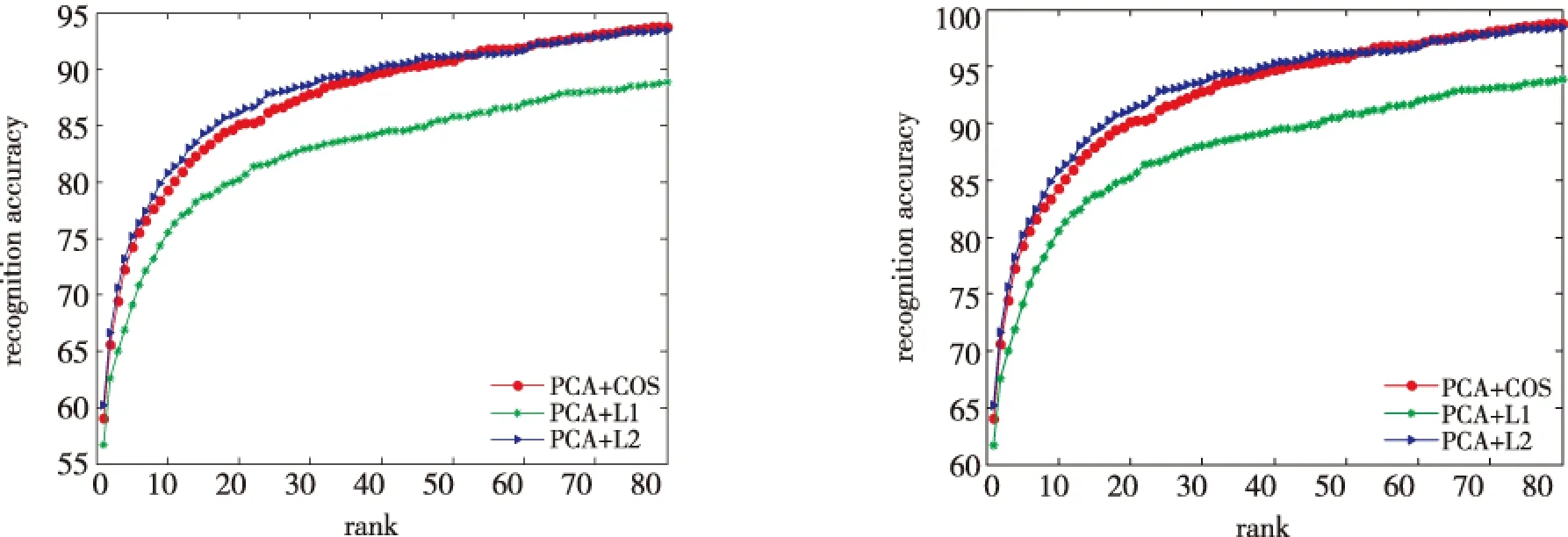
图1 PCA CMS曲线 图2 改进的快速PCA CMS曲线

4 结论与讨论

针对传统PCA方法在人脸识别应用中的一些问题，提出了一种改进的快速PCA算法进行人脸识别。实验表明，与传统PCA算法相比，本文提出的方法减少了计算时间，提高了识别率。但是，实验中针对人脸角度变换的识别效果依然不是很理想，这将是下一步研究的工作重点。