一类随机环境中单边二重生灭链的常返性

任 敏

(宿州学院 数学与统计学院,安徽 宿州 234000)

0 引 言

随机环境中的随机过程是随机过程的一个重要分支，随机环境中的随机游动(RWIRE)是它的特例，M.V.Kozlov首次提出了RWIRE[1]，其后F.Solomon研究了全直线上环境是独立同分布的RWIRE[2]，随后许多数学工作者研究了随机环境中的随机游动，取得许多成果[3-8]。作为随机环境中单边随机游动的推广——随机环境中的二重生灭链及单边二重生灭链却很少有人研究。随机环境中二重生灭链是物理学上的一个很重要的模型，具有很强的现实意义。D.Szse和S.Alili较为系统地研究了二重随机游动的若干性质[9-10]，汪荣明给出了二重生灭链的马氏性[11]，郑希民研究了独立同分布的随机环境中的单边二重生灭链的常返性[12]。本文研究在0点上具有反射壁的独立而不同分布随机环境中的单边二重生灭链的常返、正常返和零常返，给出了该生灭链的正常返和零常返的判别准则。

1 定义与符号

模型定义取值于Z+={0,1,2,…}上的随机过程{Xn,n≥0}为随机环境中的单边二重生灭链。若

P(X0=0,X1=1)=1

P(Xn+1=k|X0=0,X1=1,…,Xn-1=i,Xn=j)=Pij,k

且满足

其中0<βj,αj<1(j≥1),{βj}j≥1和{αj}j≥1分别是2列独立的随机变量。随机变量列e={βj,αj,j≥0}是随机环境，其每个现实称为环境。

因为0<βj,αj<1(j≥1)， 可知Xn是不可约二重马氏链,要讨论该二重马氏链的常返性，只需要讨论在某一点的常返性即可。不失一般性，讨论0点的常返性。

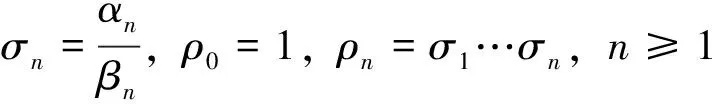
假设所讨论的随机环境e满足以下条件

条件2 存在非负递增的数列{an,n≥1}和非负且期望有限的随机变量ξ满足

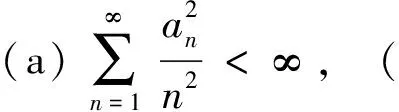
(b)P(|lnσn|>x)≤P(ξ>x),∀x≥an,∀n

(c){|lnσn|2,n≥0}是一致可积的

2 主要结果

定理1设{Xn,n≥0}是满足上述条件的随机环境e中的单边二重生灭链，若Elnσ存在，则有

(i)Elnσ≥0⟹{Xn,n≥0}常返

(ii){Xn,n≥0}非常返⟹Elnσ<0

(iii)Elnσ>0⟹{Xn,n≥0}正常返

(iv)Elnσ=0⟹{Xn,n≥0}零常返

(v)Elnσ≥0⟺{Xn,n≥0}常返

(vi)Elnσ<0⟺{Xn,n≥0}非常返

(vii)Elnσ>0⟺{Xn,n≥0}正常返

(viii)Elnσ=0⟺{Xn,n≥0}零常返

3 主要结果的证明

为证明定理给出下面几个引理

引理3[8]设{Xn,n≥0}是独立随机变量序列，若存在期望有限的随机变量X和非负数列{an,n≥0}满足

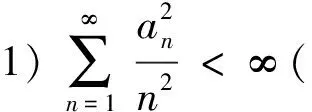
2)P(|Xn|>x)≤P(X>x),∀n,∀x≥an则有

引理4[3]设F(x)是1个分布函数，{Fn(x),n≥1}是分布函数列，f(x)和g(x)是实数集到实数集上的连续函数并且满足

如果

则有

引理5[10]在环境e满足上述条件时，则有

引理6设Xn是固定环境中的二重生灭链，则

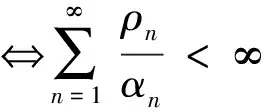
下面证明定理1。

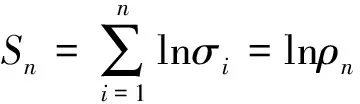
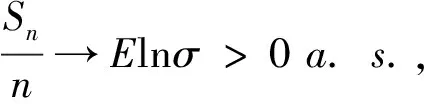
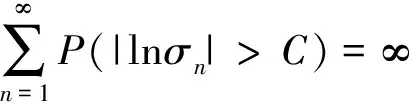
(2)定理1中结论(ii)是定理1中结论(i)的逆否命题，故定理1中结论(ii)成立。

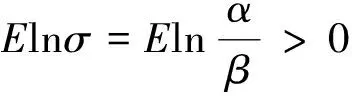
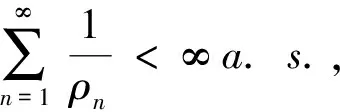
下面证明定理2。

又

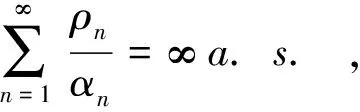
下面证明必要性。对于(v),若{Xn,n≥0}常返，则必有Elnσ≥0， 否则Eln<0由(vi)的充分性可知{Xn,n≥0}是非常返的，结论矛盾。同理(vi)的必要性成立，由定理1和定理2的结论(v)可知(vii)、(viii)成立。

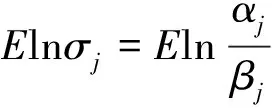
(1)Elnσj≥0⟺{Xn,n≥0}常返

(2)Elnσj<0⟺{Xn,n≥0}非常返

(3)Elnσj>0⟺{Xn,n≥0}正常返

(4)Elnσj=0⟺{Xn,n≥0}零常返

(1)Elnσ≥0⟺{Xn,n≥0}常返

(2)Elnσ<0⟺{Xn,n≥0}非常返

(3)Elnσ>0⟺{Xn,n≥0}正常返

(4)Elnσ=0⟺{Xn,n≥0}零常返

证明仅证当0

从而由引理6可知推论2中结论(2)的充分性成立。

下面证明必要性。对于推论2中结论(1)，若{Xn,n≥0}常返，则必有Elnσ≥0，否则Elnσ<0。由推论2中结论(2)的充分性可知Elnσ≥0是非常返的，结论矛盾。同理推论2中的结论(2)的必要性成立。结合推论2中的结论(1)和定理2知推论2中的结论(3)、(4)成立。