一个耀变体样本在射电波段的Jurkevich周期分析∗

米立功 谢 泉 吴忠祖 张 利 张志斌 骆娟娟

(1 贵州大学大数据与信息工程学院/物理学院贵阳550025)

(2 黔南民族师范学院物理与电子科学学院都匀558000)

(3 中国科学院上海天文台上海200030)

1 引言

耀变体(blazar)是一类极端的活动星系核(Active Galactic Nucleus, AGN), 它包含两个子类: 平谱射电类星体(Flat Spectrum Radio Quasar, FSRQ)与蝎虎天体(BL Lacertae Object, BL Lac). 耀变体在从射电波段到伽马波段的几乎整个电磁波段都显示了极强的光变, 变化时标从几小时到几年[1–6]. 在射电波段, 耀变体的光变是最早发现的特征之一[7]. 光变分析是理解耀变体物理机制的一种非常有效的方法, 通过光变分析获得的光变时标能够推出源的其他物理参数, 进而建立有效的物理模型[8–9].

根据活动星系核的统一模型[10], 耀变体的喷流方向接近观测者的视线方向. 观测表明, 在秒差距(pc)尺度, 耀变体的喷流显示了快速的向外运动, 且存在由相对论集束效应引起的视超光速运动现象[11–12]. 由于相对论集束效应, 光度L=L0δ(α+p), 这里,L0为源的内禀辐射光度,δ为多普勒因子,α为谱指数,p为多普勒增强指数[13], 其中多普勒增强指数依赖于辐射区的物理与几何[14], 多普勒因子能通过不同的方法估计[15–17].

目前, 已经有多个观测项目对大样本耀变体开展了长期的流量监测, 例如: MOJAVE(Monitoring Of Jets in Active galactic nuclei with VLBA Experiments),UMRAO(University of Michigan Radio Astronomy Observatory)等观测项目, 这为耀变体光变周期分析提供了有利条件. 有些著名的耀变体源的观测数据已积累达百年之久, 例如: 3C 273、OJ 287、BL Lacertae等, 文献[18–23]对这些源在不同的观测波段上的光变周期已经进行了深入的研究. 袁聿海等[24], 王洪涛等[25]还对诸如1ES 1959+650, 1ES 0716+714等较为常见的耀变体源进行了细致的周期分析. Fan等[26]还对一个包含168个耀变体的样本源进行了周期分析, 并发现这批耀变体显示了范围为0.08–14.5 yr的光变周期. 米立功等[27]也曾利用功率谱密度方法对59个耀变体源进行了光变周期分析.

目前, 有多种光变周期分析的方法能够应用于非均匀分布的天文观测数据[28]. 对于基于时域的周期分析, 1971年, Jurkevich[29]提出一种通过期望均方差分析来搜寻周期的方法. 1978年, Stellingwerf[30]提出了状态弥散最小化(Phase Dispersion Minimization, PDM)算法. 1985年, Simonetti等[31]提出了结构函数(Structure Function, SF)算法.1988年,Edelson等人提出了离散相关函数(Discrete Correlation Function,DCF)算法[32].1997年, Alexander[33]提出了Z变换离散相关函数(Z-transformed Discrete Correlation Function, ZDCF)算法. 对于基于频域的周期分析, Lomb等人提出了Lomb-Scargle周期图法[34–35]. 1981年,Ferraz-Mello[36]提出了时间补偿离散傅里叶变换(Date-compensated Discrete Fourier Transform, DCDFT)算法. 1995年, Foster[37]提出了CLEANest算法.2009年, Zechmeister等人提出了归一化的Lomb-Scargle算法[38].

在本文中, 我们利用欧文斯谷射电天文台(Owens Valley Radio Observatory,OVRO) 15 GHz的数据库[39], 使用Jurkevich方法分析了78个耀变体的光变曲线并估算了源中辐射区的亮温度和多普勒因子.

2 数据分析方法

2.1 数据和样本

欧文斯谷射电天文台利用40 m望远镜在15 GHz波段上的射电观测项目始于2007年,开展此项目的主要目的是为研究具有伽马射线辐射的耀变体[39–40]. 该项目的观测样本来自CGRaBS(Candidate Gamma-ray Blazar Survey),最初包含1158个北天源(J2000赤纬大于−20◦), 目前样本容量已经超过1500个. 在15 GHz波段, 该项目从2009年到2014年开展了每周大约两次的常规观测[41], 平均观测时长达8 yr之久. OVRO观测项目为研究耀变体的光变特征提供了良好的机会.

为了考察耀变体的光变周期, 首先, 我们通过目视从OVRO数据库中挑选了一批光变曲线显示了一定准周期振荡的耀变体源作为原始样本; 其次, 为了约简样本, 我们选取了红移在0.2–1.4之间, 观测时长大于7 yr的耀变体源; 最后, 我们得到78个耀变体, 包括63个平谱射电类星体与15个蝎虎天体.

2.2 Jurkevich周期分析理论

Jurkevich周期分析理论是通过分析非均匀分布的天文观测数据的期望均方差来搜寻周期的一种统计学方法. 考察一个由N个观测数据点构成的数据样本, 记样本的平均值与方差分别为¯X、S2, 则有

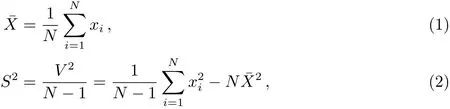
其中,xi为单个数据点,V2为样本离差平方和. Jurkevich方法将数据进行分组处理, 计算每一批分组数据的平均值, 方差与离差平方和. 如果将数据分成m组, 则第l组数据的平均值¯Xl与方差S2l分别为

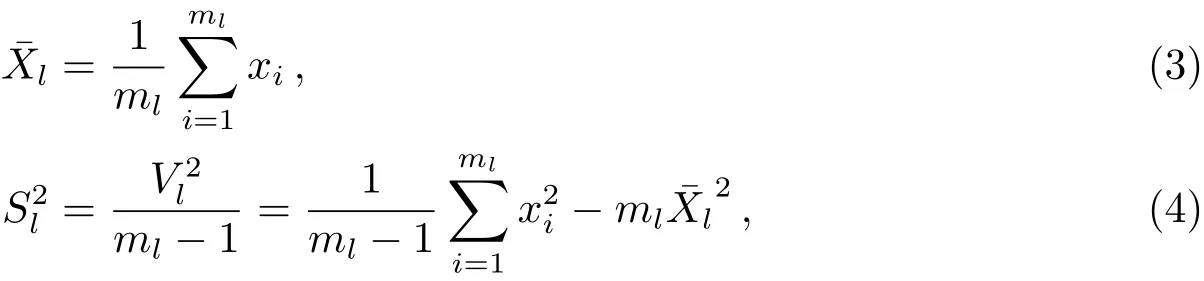
其中,ml与V2l分别为第l组数据的观测数与离差平方和. 进一步,m组数据的总离差平方和V2m为

一般而言, 各分组的平均值不相等, 此时有V2m < V2, 若各分组的平均值相等, 显然有V2m=V2, 记V2与V2m的差值为V2BG, 即

若记实验周期为P, 则对于一个给定的观测数据样本,V2不受实验周期P的影响,而V2m对实验周期P的变化十分敏感. 当实验周期P接近真实周期时,V2BG较V2m大许多, 即是说V2m相对于V2减少, 当实验周期P等于真实周期时,V2m达到最小值. 在V2m −P图中,通过寻找V2m的极小值点对应的试验周期来确定目标源的周期. 在Jurkevich方法中, 分组数越多,V2m的极小值点对应的实验周期和样本的真实周期越接近, 但分组数越多, 统计涨落越显著, Kidger等人提出了判断V2m −P图中周期真实性的f判据[42]:

其中,V2m取归一化的值. 显然, 当V2m=1时,f=0, 则表明观测样本数据没有周期性,若f≥0.5, 则表明观测样本数据具有很强的周期性, 若f <0.25, 则表明观测样本数据具有较弱的周期性. 在本文中, 我们用与V2m的最小值对应的半峰半宽(HWHM)作为周期的误差[43].

2.3 调制指数与多普勒因子

我们使用调制指数ξ描述射电源的光变幅度, 调制指数的定义如下:

其中,σs,⟨Sobs⟩分别表示流量密度的标准差与光变曲线的平均流量密度.

光变时标对源的尺寸进行了限制, 即光变区的尺寸d≥c∆t, 这里,c是光速, ∆t为光变时标, 进一步转化为角尺寸有[44–45]:

其中,z为红移,DL为光度距离. 从而可得最大角尺寸:

在观测者参考系中, 亮温度通过下面的公式给出[46]:

其中,νobs为观测频率, 以GHz为单位,Sobs是观测流量密度, 以Jy为单位, 结合(10)式与(11)式, 可获得亮温度的下限:

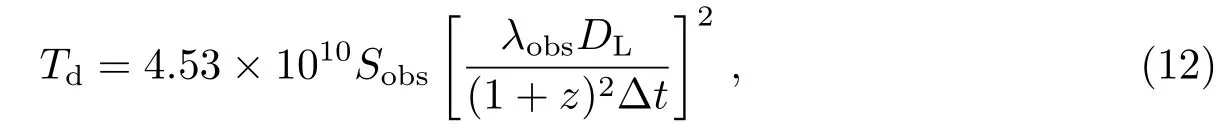
其中,λobs为观测波长, 以cm为单位. 进一步, 取与均分亮温度一致的内禀亮温度Tint=

5×1010 K[2], 多普勒因子通过下面的公式给出:

对于一个射电源, 我们取观测流量密度为光变曲线的平均流量密度, 光变时标取光变周期时标, 则得到相应的亮温度的下限, 不妨称其为特征亮温度, 进一步, 我们可以通过上面的公式估算多普勒因子的下限δd, 不妨称其为特征多普勒因子. 在表1中, 我们列出了源的特征亮温度与特征多普勒因子的计算值.

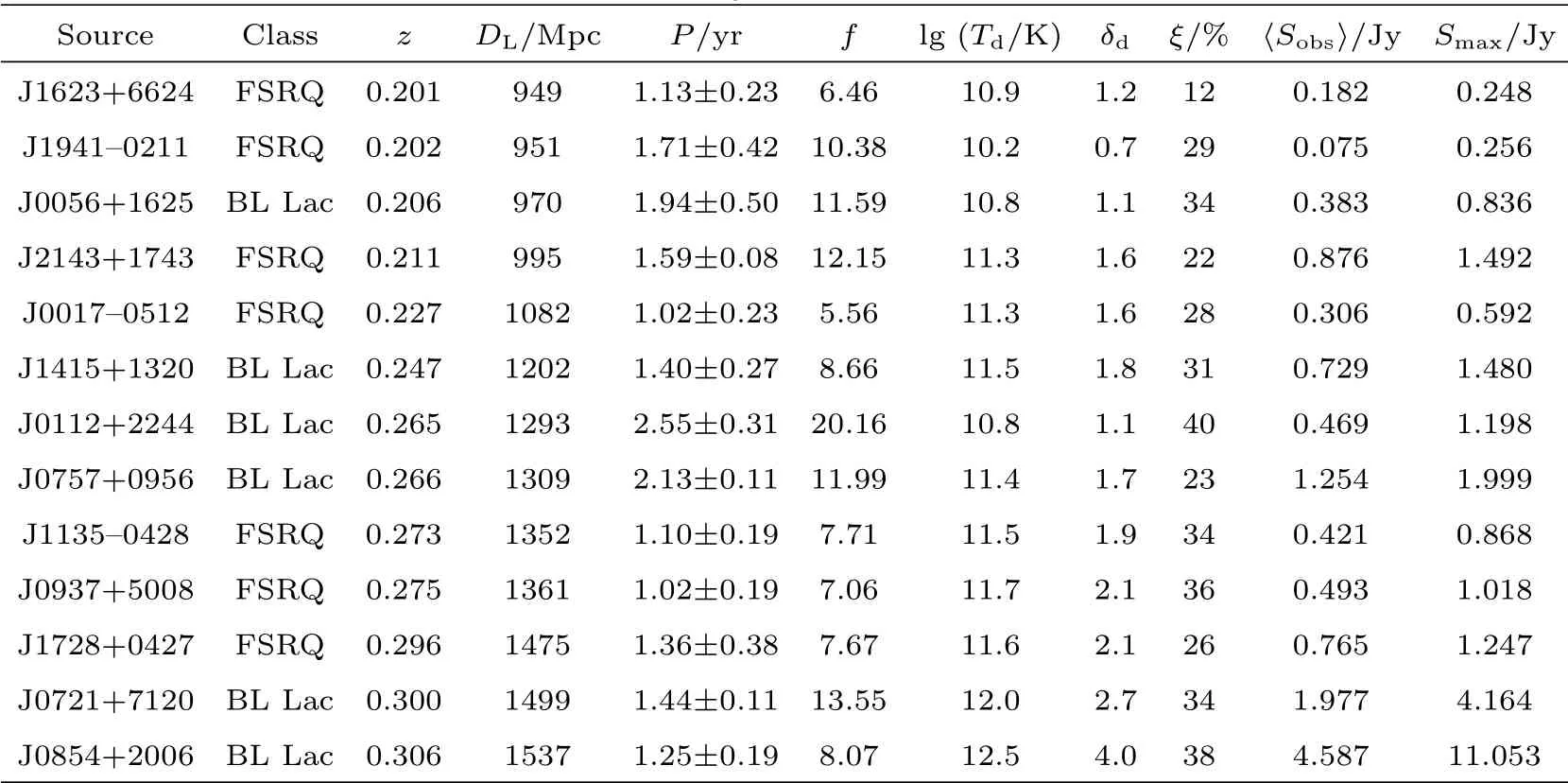
表1 78个耀变体的数据分析结果Table 1 Data analysis results of 78 blazars

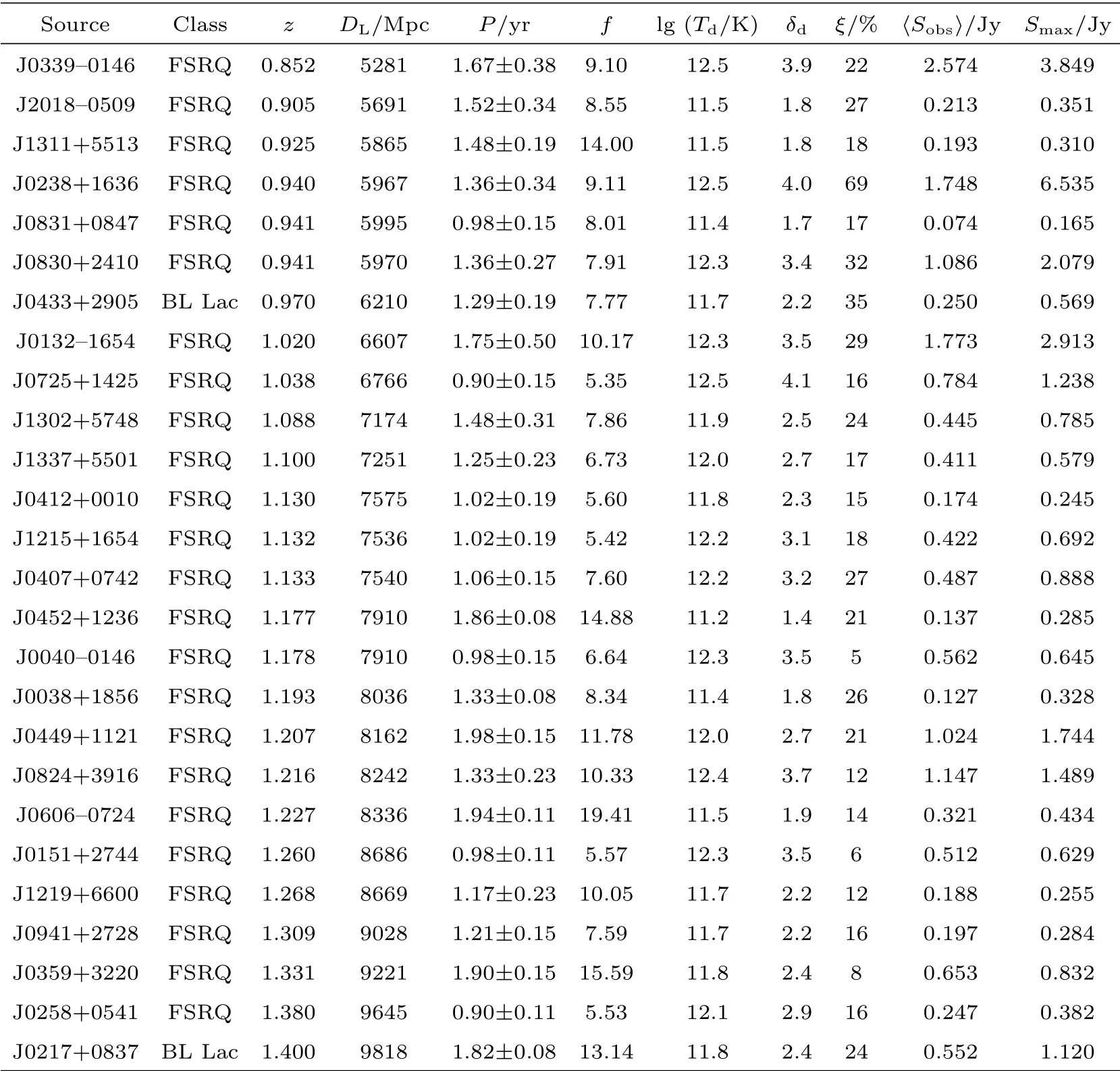
表1 续Table 1 Continued

3 结果与分析

我们利用Jurkevich周期分析理论分析了78个耀变体在15 GHz的光变曲线, 并在表1中列出了周期分析结果. 表1中1–11列分别为(1)源名(J2000); (2)活动星系核类型;(3)红移;(4)光度距离,以Mpc为单位;(5)周期,以yr为单位;(6)参数f,用于判断V2m−P图中周期的真实性; (7)特征亮温度, 以K为单位; (8)特征多普勒因子; (9)调制指数; (10)平均流量密度, 以Jy为单位; (11)最大流量密度, 以Jy为单位.

分析结果表明, 样本中的射电源显示了显著的光变周期, 周期范围为0.83–2.55 yr.利用周期时标, 我们估算了射电源辐射区的特征亮温度. 对于平谱射电类星体, 平均特征亮温度为9.4×1011K, 对于蝎虎天体, 平均特征亮温度为6.4×1011K. 在图1中,我们绘出了平谱射电类星体与蝎虎天体的特征亮温度分布图, 并通过高斯函数拟合得到相应的峰值, 结果显示: 对于平谱射电类星体, 平均特征亮温度(对数尺度)的分布峰值为(11.79±0.06)K, 略高于蝎虎天体的平均特征亮温度的分布峰值(11.41±0.09)K.对63个平谱类星体与15个蝎虎天体进行K-S检验, 结果表明在95%的置信度上, 两种分布没有显著差异.

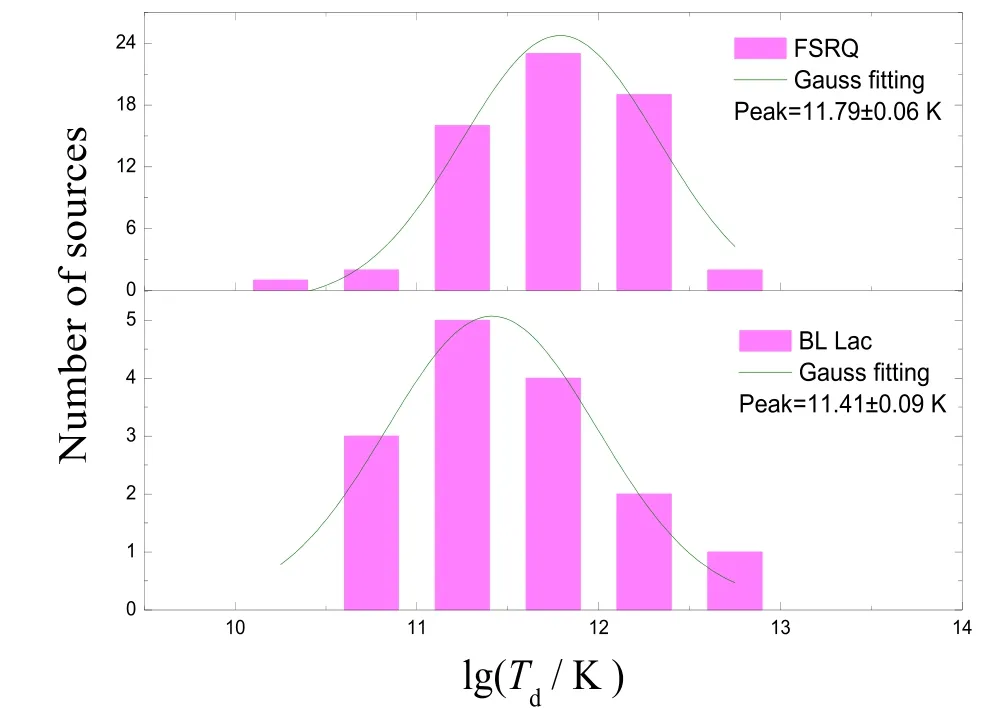
图1 FSRQ与BL Lac的特征亮温度分布图, 实线是特征亮温度分布的高斯峰值拟合.Fig.1 Distribution of lg (Td/K) for FSRQ and BL Lac, and the solid line is Gaussian peak fitting of lg (Td/K).

通过特征亮温度, 利用(13)式, 我们能够计算得到特征多普勒因子,在我们的样本中,特征多普勒因子的范围为0.7–4.1. 基于相对论集束效应, 我们推测射电流量密度和特征多普勒因子之间应该存在一定的相关性. 在图2中, 我们绘制了最大流量密度和特征多普勒因子的关系图. 相关分析表明, 射电源的最大流量密度与其特征多普勒因子具有显著的相关性, 其Spearman相关系数为0.66, 置信度≫99.99%. 通过线性拟合, 我们得到

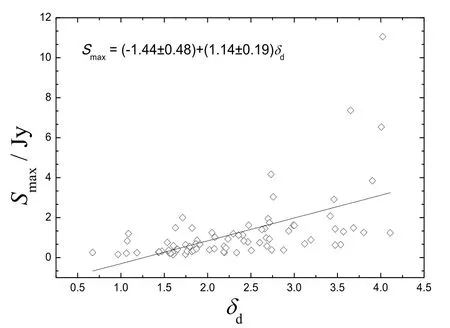
图2 最大流量密度与特征多普勒因子的相关图Fig.2 Correlation between the maximum value of flux density and the characteristic Doppler factor

调制指数用来表征射电源的光变强度, 在图3中, 我们展示了平谱射电类星体与蝎虎天体的调制指数分布, 通过K-S检验发现, 两种子类耀变体的分布并无显著不同. 但通过高斯拟合发现平谱射电类星体样本的调制指数分布峰值为19.01%±0.63%, 而蝎虎天体样本的调制指数分布峰值为27.10%±0.65%, 前者明显低于后者.

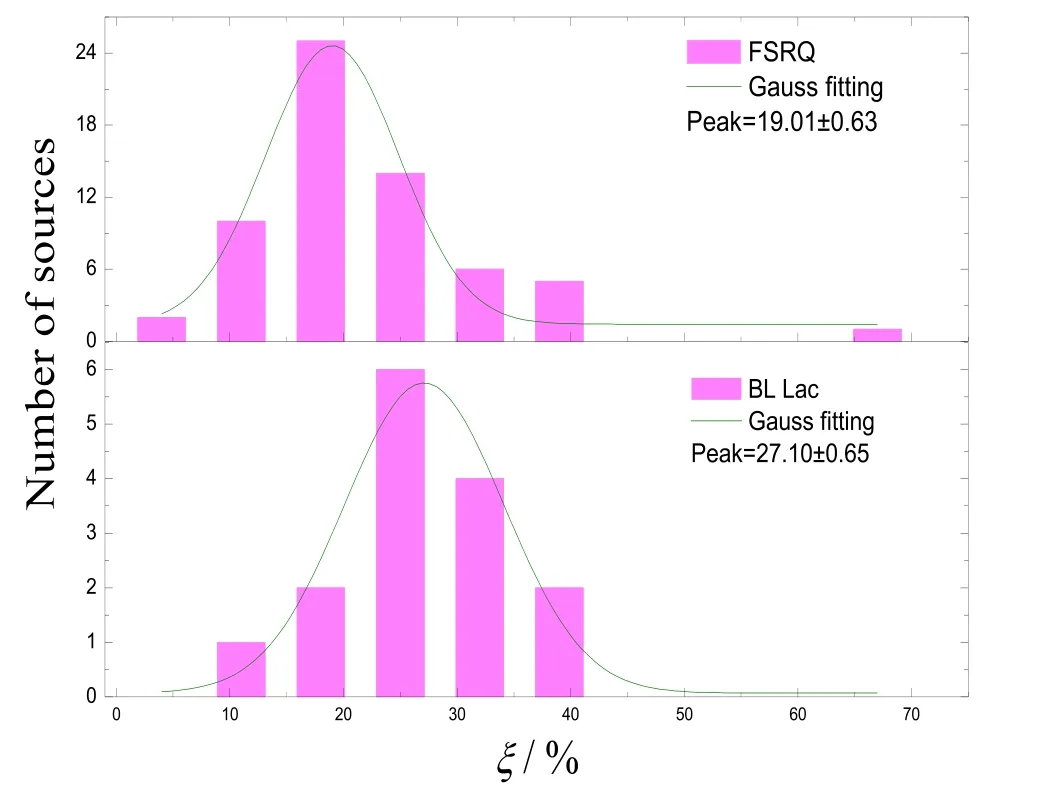
图3 FSRQ与BL Lac的调制指数ξ分布图, 实线是调制指数ξ分布的高斯峰值拟合.Fig.3 Distribution of ξ for FSRQ and BL Lac, and the solid line is Gaussian peak fitting of ξ.

4 讨论

我们利用Jurkevich周期分析方法对78个射电耀变体的光变曲线进行了周期分析, 结果表明耀变体样本的周期分布区间为0.83–2.55 yr. 从文献[47–50]中, 我们能够获得对耀变体光变周期不同的理论解释. 这些理论包括双黑洞模型、相对论集束模型、吸积盘的细盘模型等, 这些模型与活动星系核的统一模型是一致的. 在活动星系核的统一模型框架下, 星系中心存在一个超大质量黑洞, 黑洞周围环绕着一个能够触发相对论喷流形成的吸积盘. 大量观测证据表明, 活动星系核的喷流是进动的. 对于耀变体, 喷流的方向接近观测者的视线方向, 且有一个典型的4◦–6◦的视向角[51]. 视向角周期性的改变会导致观测的射电源光变曲线的周期性变化[52]. 基于双黑洞模型并假设光变周期主要源于几何效应, 则观测光变周期可表示为

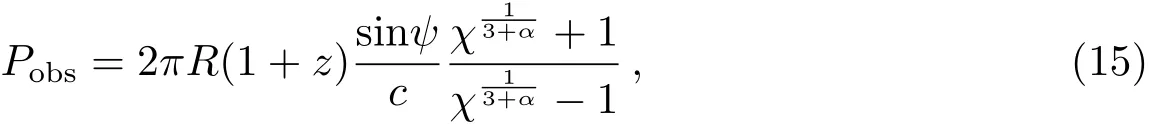
其中,R是质心距,ψ是喷流轴线与视线间的夹角,χ是观测的流量的最大值与最小值的比率. 如果M1、M2分别表示双黑洞中的小黑洞与较大的黑洞的质量, 且两者之间的距离为d, 则质心距R为进一步, 观测周期Pobs与内禀周期Pin的关系为

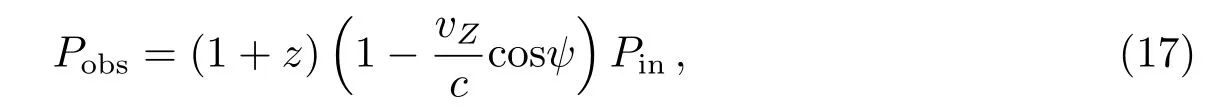
式中,vZ是沿着Z轴方向的喷流的速度大小, 对于伽玛因子Γ≃10–15之间的典型值[53],ψ=1/Γ. 对于我们的耀变体样本,z在0.201–1.400之间,Pobs在0.83–2.55 yr之间. 取Γ=10,vZ=c(1−1/Γ2)0.5, 我们能得到相应的内禀周期Pin介于37.9–201.9 yr之间.

Rieger[54]考虑了螺旋喷流模型并讨论了3种可能的周期起源情况: (1)双黑洞中轨道驱动(orbital-driven)的螺旋运动导致观测周期大于10 d; (2)内部的喷流旋转导致观测周期小于10 d; (3)进动驱动(precessional-driven)的螺旋运动导致观测周期大于1 yr, 特别是由盘内刚体进动引起的牛顿驱动(Newtonian-driven)的喷流进动可能导致观测周期Pobs≥1 yr. 对于我们的观测样本, 周期分布集中在1–2 yr之间, 因此, 可能起源于牛顿驱动喷流的进动机制.