基于条件平差的卫星双向时间传递链路性能优化方法∗
王 翔 宋会杰 王威雄 高 喆张继海 武文俊 董绍武
(1 中国科学院国家授时中心西安710600)
(2 中国科学院国家授时中心时间频率重点实验室西安710600)
(3 中国科学院大学北京100049)
(4 中国科学院大学天文与空间科学学院北京100049)
1 引言
卫星双向时间传递链路是目前精度最高的时间频率传递技术之一, 它的A类不确定度约为0.5 ns. 国际权度局(Bureau International des Poids et Mesures, BIPM)自1999年起, 正式将卫星双向时间传递(Two-Way Satellite Time and Frequency Transfer,TWSTFT)链路列为国际原子时产生的主要时间传递手段. 目前, 尽管双向链路数仅占TAI (International Atomic Time)总链路的12%, 却传递了超过60%权重的钟数据以及大部分用于TAI计算的一级频标数据. 因此改善TWSTFT链路的稳定性意味着改善TAI和协调世界时(Coordinated Universal Time, UTC)的不确定性[1].
近年来, 许多机构、学者就提高卫星双向时间传递链路的短期稳定度水平、降低周日效应影响的问题展开了专项研究. 2010年中国台湾的中华电信股份有限公司(Telecommunication Laboratories, TL)的Tseng等人, 利用时间传递网络中的冗余链路建立了两个守时实验室之间的间接时间传递链路, 提出一种将卫星双向时间传递网络中的直接链路与间接链路相结合的方法, 显著降低了测量噪声, 提高了链路的短期稳定度水平[2]. 2017年中BIPM的Jiang等人分析了欧洲卫星双向时间传递链路, 提出周日效应是TWSTFT链路不稳定的主要原因之一, 指出通过使用中继实验室进行两个守时实验室之间的间接比对, 能够有效降低周日效应的影响[3].
一直以来,参与TAI计算的TWSTFT实验室通过国际时间频率咨询委员会(Consultative Committee for Time and Frequency, CCTF) TWSTFT工作组制定的时间表在规定的时间段进行相互比对, 其中任意两条比对链路都是相互独立的, 它们的测量误差主要是由TWSTFT链路设备硬件、数据处理方法(如插值等)、测量不确定度及其他具有周期变化的因素(如温度变化)引起的, 会造成TWSTFT链路稳定度降低和周日效应现象.
从2017年3月开始, 亚欧卫星双向时间传递链路开始使用俄罗斯ABS-2A卫星通过亚太区域波束进行工作. 中国参与TAI计算的具有TWSTFT链路的两个实验室中国科学院国家授时中心(NTSC)和中国计量科学研究院(NIM)都处于该波束覆盖区域的边缘,尤其是NTSC处于辐射区域的外围. 这意味着将有更大的测量噪声影响NTSC的国际时间传递工作.
对于每一条参与TAI计算的TWSTFT链路, 总可以找到若干个与之相关的几何三角网络, 网络中包含两条TAI计算链路及一条非TAI计算链路, 其中TAI计算链路是国际卫星双向时间传递枢纽站德国联邦物理技术研究所(Physikalisch-Technische Bundesanstalt, PTB)与TAI实验室之间的时间传递链路, 对于每一个三角网络, 各链路测量结果的矢量和应该是0. 然而受到测量误差的影响, 三角网络测量结果的闭合差最终反映了网络内各链路测量误差的矢量和, 这就形成了网络内链路测量结果的一个约束条件. 为了弱化测量噪声对待优化链路的影响, 本文基于平差理论, 提出了一种基于条件平差的卫星双向时间传递链路性能优化方法. 上述三角网络中的TAI计算链路由BIPM不定期进行校准, 非TAI计算链路未经BIPM校准, 因此在组建优化网络前, 需要先对非TAI计算链路进行校准.
待优化链路性能的优化过程可以分为两个步骤: 对未经校准的链路实施校准, 分析校准后各链路性能, 依据性能指标组建优化网络; 用优化网络内各链路数据建立条件平差[4–5]方程, 获得每条链路的最优估计. 该优化方法与传统的卫星双向时间传递方法相比, 能够有效提高待优化链路的短期稳定度, 同时降低周日效应对测量结果的影响.
2 组建优化网络
对于每一条TWSTFT TAI计算链路, 都能找到两条链路与它形成几何三角形, 在三角形中, 与国际时间传递中心站PTB相关的两条链路在参与TAI计算前, 都经过了BIPM的校准, 另一条未经BIPM校准的TWSTFT链路, 在进行数据处理分析之前, 应该进行校准. 目前, BIPM的TWSTFT链路校准可以通过卫星双向时间传递移动校准器进行直接校准, 也可以通过GPS (Global Positioning System) PPP (Precise Point Positioning solutions)链路实施间接校准. 文中采取第2种方式对未经校准的TWSTFT链路进行校准.
2.1 TWSTFT链路校准方法
在卫星双向时间传递几何三角网络中, 存在部分没有校准的链路, 为了提高测量结果的准确度, 需要对未经校准的链路进行校准. 自从2001年加拿大的Kouba等人提出GPS PPP算法[6–12]以来, 随着IGS (International GNSS (Global Navigation Satellite System) Service)轨道精度和精密钟差精度的提高(目前轨道精度已达2.5 cm, 钟差精度优于0.1 ns[13–14]), 电离层、固体潮等相关物理模型的优化, PPP的A类时间传递不确定度已达0.3 ns[15–17]. 由于GPS PPP具有高分辨率、高精度的特点, 当没有校准器可以实施直接校准的时候, 对于GNSS链路的校准能够转移到双向链路, 可以用校准过的GNSS链路校准双向链路.
如图1所示,使用已校准的GPS PPP链路对TWSTFT链路进行校准[18–20]. 本地相位微调仪输出的UTC(k)的物理实现信号分别是1 PPS (Pulse Per Second)脉冲和5 MHz频率信号. 由于已校准接收机、待校准调制解调器使用的频率标准为10 MHz, 因此使用倍频器, 将频率变为10 MHz. 本地已校准GPS PPP链路中的接收机、待校准TWSTFT链路中的调制解调器的初同步秒信号使用相位微调仪输出的1 PPS脉冲信号, PTB的连接类同, 在本地实验室与PTB之间采用同源信号, 使用GPS PPP和TWSTFT原理, 建立两条独立的时间传递链路. 对于GPS PPP链路, 测量得到UTC(k)与IGS系统时间IGST(International GNSS Service Time)的偏差, 通过数据传输网络交互各自的测量结果数据, 得到UTC(k)与UTC (PTB)的钟差Dppp. 对于TWSTFT链路, 依据卫星双向时间传递原理[21–22], 使用GEO (Geostationary)卫星测得单边数据后, 通过数据传输网络交互经过2次拟合的观测数据, 得到UTC(k)与UTC (PTB)的钟差Dtwstft. 将Dppp时间序列以Dtwstft的时标为参考进行插值[23], 得到Dcppp.Dcppp与以Dtwstft之差即为单次校准值,记为C=Dcppp−Dtwstft. 校准值即为单次校准值的平均值. 为了提高校准值的准确度,我们至少需要7 d的连续测量数据.
2.2 优化网络的组网方法
根据平差理论, 测量平差是依据指定的最优化规则, 由一系列带有测量误差的观测数据, 求得未知量最佳估计的方法. 若记守时实验室A、B之间的TWSTFT链路为待优化链路, 组建优化网络就是指以待优化链路为中心, 寻找与待优化链路具有几何三角关系的链路, 分析链路性能, 以各链路测量噪声指标及谱分析[24]指标为依据, 使待优化链路相关指标水平在网络中最低.如图2所示, A、B、C站都是参与TAI计算的守时实验室,使用同一颗卫星进行双向时间传递, 若记A站实现的UTC物理信号为UTC(k_1), B站实现的UTC物理信号为UTC(k_2), C站实现的UTC物理信号为UTC(k_3), 则经链路AB可获得UTC(k_1)−UTC(k_2), 其他链路类同. 当链路AB作为待优化链路时, 在与它相关的几何三角网络中逐一排查, 选择能够满足条件的网络作为优化网络.

图1 TWSTFT链路校准连接Fig.1 Connection of TWSTFT link calibration
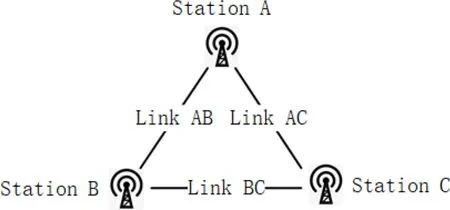
图2 优化网络结构Fig.2 Structure of optimized network
3 条件平差模型的建立与求解
本节根据卫星双向时间传递的实际情况, 从权系数阵设置方法[25–26]开始, 介绍了条件平差模型的建立与求解方法.
3.1 权系数阵的设置方法
卫星双向时间传递链路经过校准后, 就可以忽略链路系统差对时间传递结果的影响. 在此基础上, 使用Vondark滤波对3条链路的数据进行滤波, 以链路数据与滤波结果的标准差为依据, 确定各链路的权. 显然, 链路标准差与链路权重成反比例关系. 权的设置为:

以第i条链路为例, 链路标准差表示为Si, 共有n个测量数据Xj, 为第j个测量数据,XjVondark为相应的Vondark滤波值. 取标准差的倒数作为链路取权因子, 记为pi.ωi为链路的权. 3条链路的总权重为1.
由于3条TWSTFT链路相互独立, 即链路之间的协方差为零, 因此权系数阵记为

其中ωAB为AB链路的权重,ωBC为BC链路的权重,ωCA为CA链路的权重. 显然, 链路越稳定, 它在平差模型中所占有的权重越大, 对平差结果的影响越大.
3.2 条件平差模型的建立与求解方法
在上述的优化网络中, A、B、C站均为参与TAI计算的TWSTFT站点, 使用2.1节的校准方法对网络中的3条TWSTFT链路实施校准, LinkAB是A站与B站之间的卫星双向时间传递链路, 用于直接测量A、B两站钟差UTC(k_A)−UTC(k_B), LinkBC、LinkCA类同. 实际测量中, 受测量误差的影响, 测量值与真值存在一定的偏差, 如下:

其中LinkAB的测量值表示为LAB, 真值的估计值表示为AB, 测量误差估计值表示为vAB. 3条链路测得的钟差都可以使用BIPM FTP (File Transfer Protocol)服务器上更新的卫星双向ITU (International Telecommunications Union)数据文件, 依据卫星双向时间传递原理计算获得. 由于各链路的测量过程都是相互独立的, 理论上它们的闭合差应当是0, 于是可以建立条件方程,

其中a1、a2、a3分别是3条链路的测量状态系数. 若记ω为条件方程的闭合差, 将(3)式代入(4)式后可得:
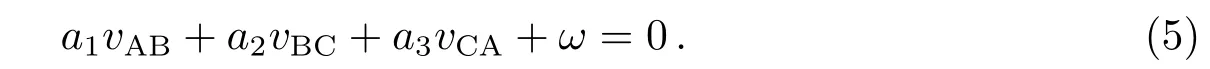
由于3条链路的测量条件相同, 因此上式中a1=a2=a3=1.ω由3条链路测量值计算得到. 令

则(4)式、(5)式可写为

由于(7)式中误差估计值存在无穷多解, 根据最小二乘原理, 在解集中存在一正定矩阵P,当满足VTP V取最小值时, 设其联系数向量为U1,1=[u]T, 可用拉格朗日乘数法, 得到新的函数
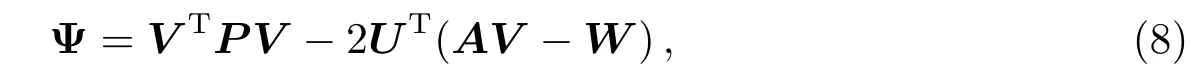
其中P可由3.1节所述方法获得. 将Ψ对V求一阶导数, 并令其为0, 得
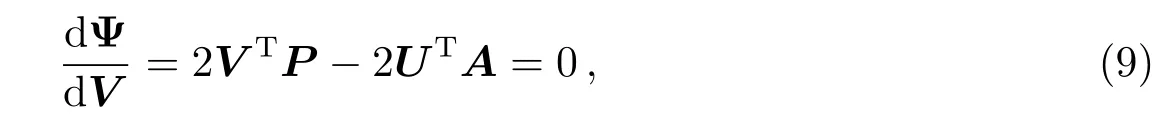
解(9)式可得误差估计值方程

将(10)式代入(7)式, 可得

其中A、P、W已知. 解(11)式, 可得

将(12)式代入(10)式, 可得唯一一组误差估计值. 将误差估计值代入(3) 式, 可得链路真值的估计值.
4 结果分析
实验选取NIM-NTSC卫星双向时间传递链路作为待优化链路, 以NTSC、NIM以及PTB之间的TWSTFT链路组成优化网络, 对优化网络的组网方法和条件平差模型进行实验验证. 选择了2018年10月1—29日PTB-NTSC、PTB-NIM、NIM-NTSC的GPS PPP和TWSTFT链路数据进行分析. 依据3.1节权系数阵设置方法, 设置权系数阵如下

PTB-NTSC链路在平差模型中所占权重为0.2818, PTB-NIM链路在平差模型中所占权重为0.5534, NIM-NTSC链路在平差模型中所占权重为0.1648.
4.1 TWSTFT链路校准结果
为了确定校准结果的性能,依据TWSTFT链路时间传递结果的时标,对GPS PPP链路的时间传递结果进行插值, 将两者一次差分后的残差如图3–5所示, 分别是PTBNTSC、PTB-NIM和NTSC-NIM的TWSTFT链路的校准残差直方图, 显然残差均为服从近似正态分布的随机序列, 均值为0. 方差处于TWSTFT链路与GPS PPP链路的合成不确定度范围内, 校准结果可信.

图3 PTB-NTSC TWSTFT链路校准残差直方图Fig.3 PTB-NTSC TWSTFT link calibration residual histogram

图4 PTB-NIM TWSTFT链路校准残差直方图Fig.4 PTB-NIM TWSTFT link calibration residual histogram
校准后, 平差网络内3条链路的闭合差分布如图6所示, 经检验闭合差服从均值为0.3955 ns, 方差为0.2703 ns2的正态分布. 说明此时平差网络内各链路测量结果的不确定度主要来源于随机误差的影响, 可以使用测量平差模型抑制随机误差.
4.2 一致性分析
在优化网络中, 各站GPS PPP链路与TWSTFT链路相互独立, 因此将平差前后的TWSTFT链路测量数据与相应的GPS PPP链路测量数据相比较, 若两条链路的测量偏差处于测量不确定度允许的范围内, 则可以说明平差后TWSTFT链路测量结果与GPS PPP链路测量结果是一致的.

图5 NIM-NTSC TWSTFT链路校准残差直方图Fig.5 NIM-NTSC TWSTFT link calibration residual histogram

图6 TWSTFT平差网络测量结果闭合差图Fig.6 Closure error diagram of TWSTFT adjustment network measurement results
两站之间TWSTFT链路与GPS PPP链路的测量结果存在一定的偏差, 这主要是由两条链路各自的测量不确定度造成的, 偏差的波动范围取决于链路不确定度的大小, 若以标准差作为链路不确定度的估计值, 依据不确定度传播律, 两条链路的最大偏差可表示为两条链路测量结果标准差平方和的算术平方根. 也就是说, 若偏差处于正负最大偏差范围以内, 则可判定两条链路的测量结果一致.
图7是NIM-NTSC平差前后链路测量结果与BIPM发布的T公报(Circular T) Cirt.370比较图, 可以看出平差前后的TWSTFT链路和GPS PPP链路都与BIPM公布的Cirt.370的趋势相符合.
NIM-NTSC TWSTFT链路的测量不确定度约为1.86 ns, NIM-NTSC GPS PPP链路的测量不确定度约为1.43 ns, 两条链路的最大偏差约为2.35 ns. 图8是NIM-NTSC平差前后TWSTFT链路测量结果与GPS PPP链路测量结果偏差的分布图, 可以看到两条链路平差前最大偏差绝对值约2.55 ns, 平差后的最大偏差绝对值约2.34 ns. 平差后NIM-NTSC的TWSTFT链路与GPS PPP链路测量结果的偏差处于不确定度允许的范围之内.
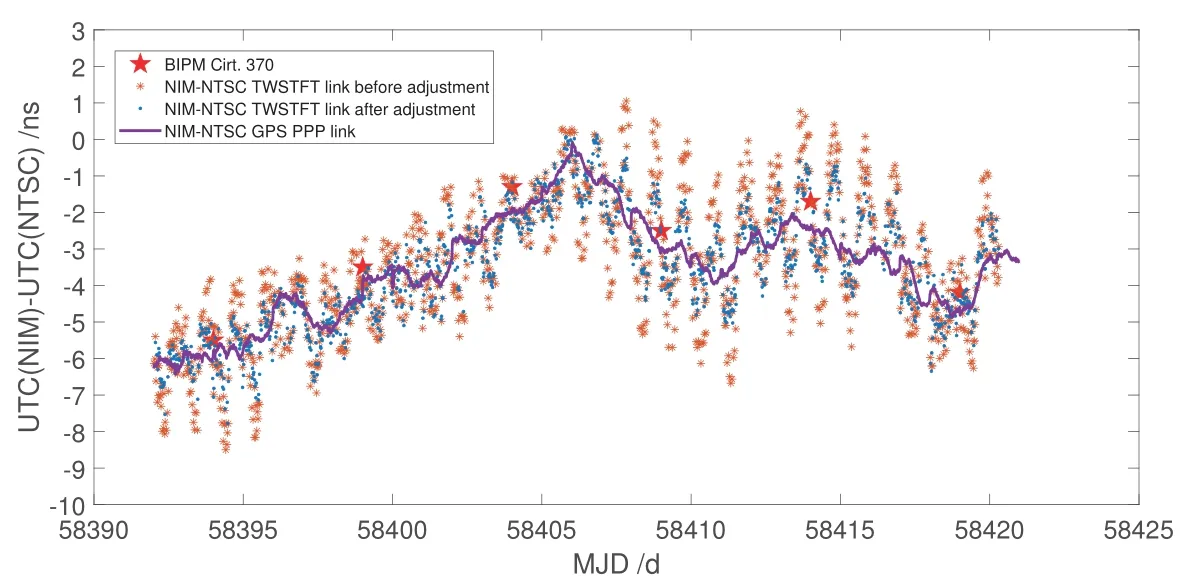
图7 NIM-NTSC平差前后链路测量结果与BIPM Cirt.370比较Fig.7 Comparison of NIM-NTSC link before and after adjustment with BIPM Cirt.370

图8 平差前后NIM-NTSC TWSTFT链路与GPS PPP链路测量结果偏差Fig.8 Measurement results deviation of NIM-NTSC TWSTFT link with GPS PPP link before and after adjustment
网络内,其他链路的性能参数如表1所示,可知PTB-NIM和PTB-NTSC的TWSTFT链路与GPS PPP链路测量结果在不确定度范围内都是一致的.
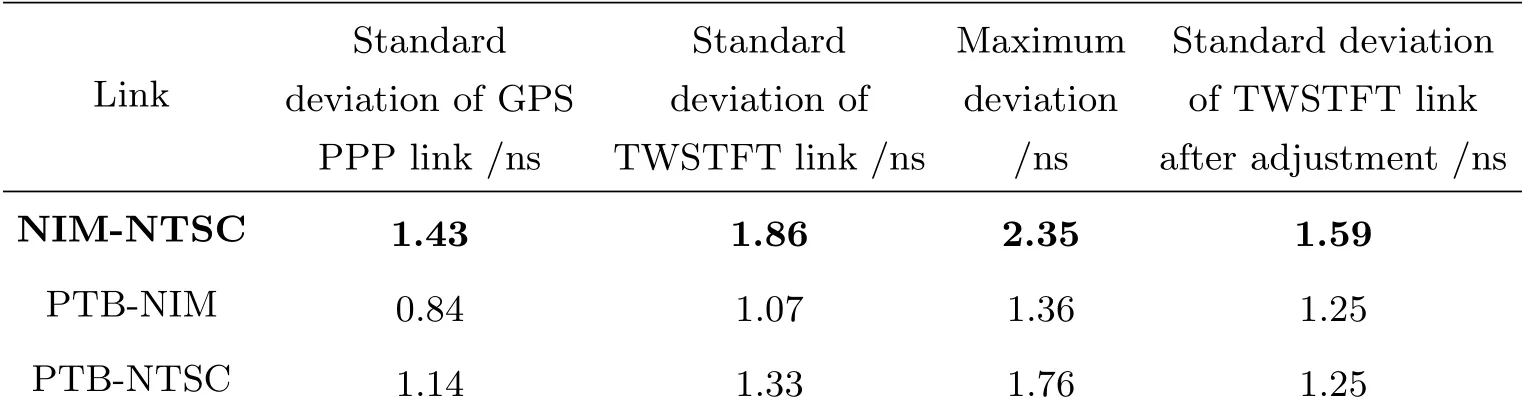
表1 GPS PPP和TWSTFT时间传递链路性能参数Table 1 Performance parameters of the GPS PPP and TWSTFT time transfer link
4.3 稳定度分析
为了检验平差方法对网络平差后各链路稳定度的影响, 分别以Allan方差、时间方差作为标准进行评估.
图9虚线是平差前NIM-NTSC链路的Allan方差分析结果, Tau为平均时间, 可以看到, 实线是平差后NIM-NTSC链路的Allan方差分析结果. 平差前、后半小时稳定度提高约64.6%, 1 h稳定度提高约13.7%, 2 h稳定度提高约20.2%, 4 h稳定度提高约22.9%, 8 h稳定度提高约35.1%, 16 h稳定度提高约28.4%, 32 h稳定度提高约19.1%.
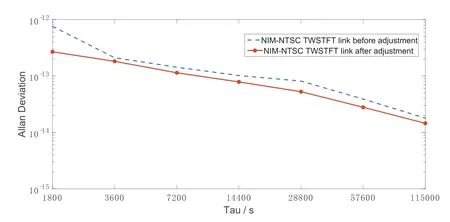
图9 平差前后NIM-NTSC TWSTFT链路Allan方差Fig.9 Allan deviation of NIM-NTSC TWSTFT link before and after adjustment
图10虚线是平差前NIM-NTSC链路的时间方差(TDEV)分析结果, 实线是平差后NIM-NTSC链路的时间方差分析结果. 平差前、后半小时时间方差降低约64.6%, 1 h时间方差降低约11.6%, 2 h时间方差降低约12.1%, 4 h时间方差降低约27.4%, 8 h时间方差降低约41.6%, 16 h时间方差降低约28.3%, 32 h时间方差降低约26.3%. 具体数值结果如表2所示.

图10 平差前后NIM-NTSC TWSTFT链路时间方差Fig.10 Time deviation of NIM-NTSC TWSTFT link before and after adjustment
上述比较发现, 卫星双向时间传递网络中待优化链路的时间稳定度和频率稳定度都有不同程度的提高, 这是由于在时间域平差, 就是将测量误差进行分摊. 为了降低网络中各链路的性能差异, 需要设置合适的权系数阵, 这决定了网络中各链路总的测量误差分摊到各链路的系数. 待优化链路测量结果加入平差值后原测量误差减小, 具体体现为测量结果稳定度提高, 时间方差降低.

表2 NIM-NTSC TWSTFT链路平差前后稳定度统计Table 2 The stability statistics of NIM-NTSC TWSTFT link before and after adjustment
4.4 谱分析
为了量化周日效应对TWSTFT链路时间传递结果的影响, 通过谱分析对结果中的频率分量进行标定. 采用上述观测数据, 图11、12是NIM-NTSC双向链路平差前后的频谱分析结果, 其中分别标示了24 h分量(周日效应引起)、12 h分量、8 h分量和6 h分量.平差前后待优化链路24 h分量降低约24.6%.
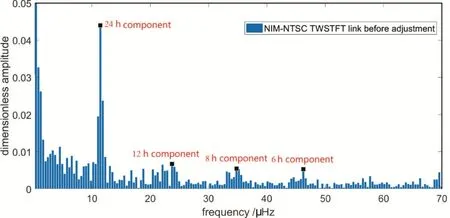
图11 NIM-NTSC双向链路平差前频谱分析Fig.11 Spectrum analysis of NIM-NTSC TWSTFT link before adjustment
网络中, 平差前后3条链路频谱分析中24 h分量的幅度见图13, 可知PTB-NIM TWSTFT链路平差前后24 h分量(周日效应引起)增大约214.8%, PTB-NTSC TWSTFT链路平差前后24 h分量增大约10%, NIM-NTSC TWSTFT链路平差前后24 h分量降低约24.6%, 相应的谱分析结果见表3, 其中各分量幅度都已经过归一化处理.
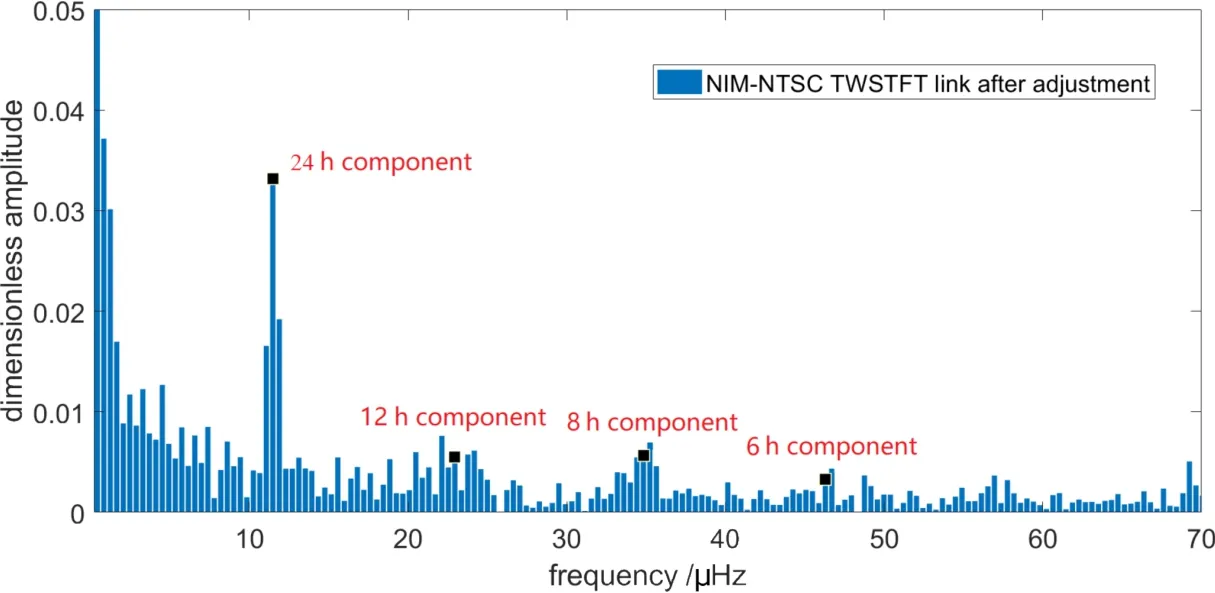
图12 NIM-NTSC双向链路平差后频谱分析Fig.12 Spectrum analysis of NIM-NTSC TWSTFT link after adjustment
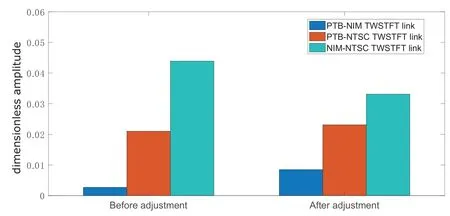
图13 平差前后链路频谱分析中24 h分量幅度Fig.13 24-hour component magnitude in link spectrum analysis before and after adjustment
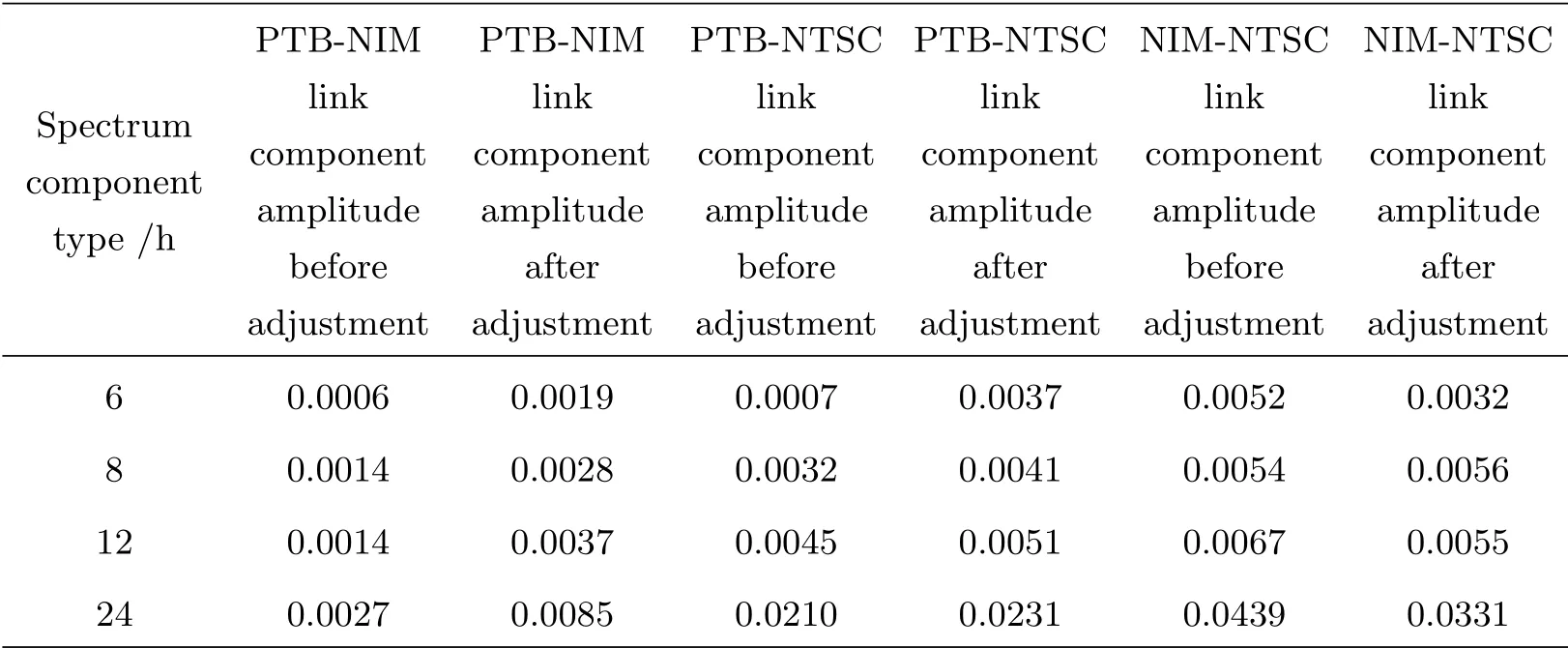
表3 平差前后链路频谱分析各分量幅度统计Table 3 Statistics of each component amplitude for link spectrum analysis before and after adjustment
上述比较发现, TWSTFT链路周日效应引入的24 h分量越大, 平差处理对周日效应的改善也越大. 平差算法不能消除周日效应对卫星双向时间传递网络中各链路的影响,而是将其分摊. 优化网络中待优化链路受周日效应影响最大, 平差后周日效应对它的影响降低最多. 这说明随机误差也是影响卫星双向时间传递周日效应量级的一个因素.
5 结论
为了提高卫星双向时间传递链路的短期稳定度水平, 弱化周日效应的影响, 提出了一种基于条件平差的卫星双向时间传递链路性能优化方法, 首先采用优化网络建立方法, 组成具有几何三角关系的卫星双向时间传递网络, 再对网络中各链路进行校准, 最后建立平差模型, 实现待优化链路的优化. 通过实验分析, 平差后待优化链路的短期稳定度指标大幅提高, 也明显降低了周日效应对待优化TWSTFT链路的影响. 对于待优化链路而言, 不需要新增设备或是改造现有链路设备, 只要在其几何三角网络中存在性能优于待优化链路性能的链路, 就能使用该方法优化链路性能. 对提高TWSTFT链路性能具有重要意义.

