LAMOST一维光谱提取算法的分析与比较∗

李 敏 李广伟 吕 科 段福庆哈斯铁尔·哈尔肯 赵永恒

(1 中国科学院大学工程科学学院北京100049)

(2 中国科学院国家天文台光学天文重点实验室北京100101)

(3 中国科学院国家天文台空间天文与技术重点实验室北京100101)

(4 北京师范大学人工智能学院北京100875)

1 引言

LAMOST (Large Sky Area Multi-Object Fiber Spectroscopic Telescope, 大天区面积多目标光纤光谱望远镜, 又名郭守敬望远镜)是我国自主研发的首台天文大科学装置[1–4], 目前已经获取超过一千万条的光谱, 其中高质量光谱超过九百万条. 它构建了世界上最大的恒星光谱数据集, 填补了中国大型天文基础数据的空白, 同时为国内外124所科研机构和大学的近800位用户提供了科研帮助, 加强了国际国内在天文方面的合作[5].

光谱提取作为LAMOST 2维数据处理的一个重要环节, 对1维抽谱结果的质量起到了至关重要的作用[6]. 高质量的1维光谱可以帮助科研工作者更好地了解目标天体的物理属性和特征___[7–8]. 本文针对LAMOST的2维光谱图像, 从信噪比和分辨率的角度, 分析并比较了孔径法、轮廓拟合法、直接反卷积方法、基于Tikhonov正则化的反卷积抽谱算法、基于自适应Landweber迭代的反卷积抽谱算法以及基于Richardson-Lucy迭代的反卷积抽谱算法这6种抽谱算法.

2 抽谱算法

本小节结合LAMOST 2维光谱图像详细介绍了孔径法、轮廓拟合法、直接反卷积方法、基于Tikhonov正则化的反卷积抽谱算法、基于自适应Landweber迭代的反卷积抽谱算法以及基于Richardson-Lucy迭代的反卷积抽谱算法这6种抽谱算法. 其中, 孔径法、轮廓拟合法和直接反卷积方法是传统的经典抽谱算法. 基于Tikhonov正则化的反卷积抽谱算法、基于自适应Landweber迭代的反卷积抽谱算法以及基于Richardson-Lucy迭代的反卷积抽谱算法是正则化的反卷积抽谱方法.

为了便于表述, 本文约定: 对于LAMOST的CCD (Charge-Coupled Device)而言, 行的方向平行于光纤的空间排列方向; 列的方向代表2维光谱的色散方向, 即波长方向.

2.1 孔径法

最早的抽谱算法孔径法[9](Aperture Extracion Method, AEM)是由测光数据处理发展而来的. 其主要想法就是: 把目标光谱扩散出去的光子能量再重新收集起来.

具体做法是: 在给定波长处将光通量在空间方向上固定大小的孔径中积分, 所得到的积分值就是该波长处的流量值. 1维抽谱结果就是这些积分值沿波长方向的排列. 如图1所示, 孔径的大小关系到光谱流量提取的准确性, 图中孔径大小为2N+1,N表示孔径边缘到中心的距离. 一般孔径的宽度大于光谱轮廓的半高全宽, 而小于相邻两条光纤的间隔距离.

图1 孔径法原理示意图Fig.1 Sketch illustration of the aperture extraction method

基于孔径法的光谱流量抽取算法可以通过下式进行描述:

其中,Fi表示CCD上第i行光谱的总流量值;Dij表示第i行第j列像素的流量值;xcen表示光谱轮廓的中心位置; 孔径的宽度为2N+1.

可以看出: 孔径法抽谱的优点是简单快速、便于操作; 缺点是孔径的大小很难确定.孔径太小, 有用的信息会被丢失; 孔径太大, 又会引入噪声和相邻光纤的交叉污染.

2.2 轮廓拟合法

轮廓拟合法[10](Profile-Fitting Method, PFM)认为2维光谱图像是1维目标光谱和空间轮廓的乘积. 该方法通常采用假定的轮廓模型函数(通常是高斯函数)对空间方向上的轮廓逐行拟合[11], 给定波长处的光通量就是对应行的拟合值.

假设2维光谱图像在空间方向的归一化解析轮廓为函数ϕ(j), 则对于CCD上的第i行,可以利用下式抽谱:

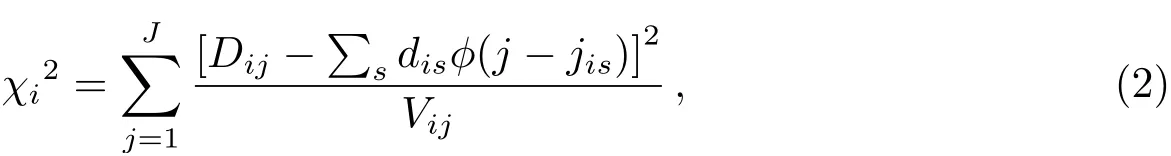
其中,χi2表示第i行真实流量值和拟合值之间的误差平方和;jis是第i行第s条光谱的中心位置;dis是第i行第s条光谱的真实流量值, 即要求解的值;Dij是第i行第j列像素的流量值;Vij是第i行第j列像素的流量值方差;J是CCD的总列数.

与孔径法相比, 轮廓拟合法更加细致地刻画了轮廓在空间方向的变化. 但是它有一个很苛刻的要求: 中心处于光谱上任何波长处的点扩散函数(Point Spread Function,PSF)I(x,y)可以分解为独立的两个函数Ix(x)和Iy(y),即I(x,y)=Ix(x)Iy(y).其中,Ix(x)表示该PSF在x方向的函数表达;Iy(y)表示该PSF在y方向的函数表达. 这里的PSF是指单色光经过光学仪器后在CCD上呈现的2维轮廓, 它是光纤在CCD上成的像,是由光纤初涉段的像经过仪器轮廓造成的. 也就是说, 如果PSF具有2维高斯轮廓, 且高斯轮廓的两个主轴都平行于CCD的行和列, 则该PSF满足上面的苛刻条件. 但是, 处于CCD上的PSF一般都不具有这样的形式. 那么, 2维光谱横截面的轮廓就不再是固定的, 而是取决于1维输入光谱本身的细节信息. 如果光谱在波长方向变化缓慢, 那么对抽谱结果的影响不大; 但是, 当光谱中存在许多尖锐特征的时候, 轮廓拟合法的1维抽谱结果就变得不确定了.

同时CCD光谱图像的信噪比对该方法有很大影响, 大视场相机拍摄到的CCD光谱图像的空间轮廓变化剧烈, 尤其在强发射线和吸收线的位置. 因此, 如何对每条光纤选择合适的轮廓拟合函数仍是一个棘手的问题, 不当的拟合函数可能引入更多的误差.

2.3 直接反卷积法

Bolton和Schlegel[12]提出了采用直接反卷积的方法(Bolton and Schlegel Deconvolution Method, BDM)进行抽谱. 传统的抽谱方法将2维光谱图像看作是观测源本身的流量模型, 但是这个模型并没有去除仪器的轮廓. 文献[12]把2维光谱图像看作是1维目标光谱卷积上仪器的轮廓即PSF, 原理如图2所示, 图中⊗是卷积符号, 表示卷积运算.

该算法对2维光谱图像重新建模, 更加准确地反映了CCD图像中入射光谱转化为光子计数的方式, 克服了传统抽谱方法的系统缺陷. 具体建模如下: 单色光束经过光学仪器然后在CCD上留下钟型的PSF. 单根光纤的2维光谱图像可以看做是不同强度的PSF在波长方向上的叠加:

其中,f(x,y)和η(x,y)分别表示在CCD上(x,y)处的光谱流量值和噪声流量值;g(λ)是波长λ处的真实流量,就是我们要抽谱得到的流量;hλ(x,y)是波长λ处的PSF在CCD上(x,y)处的值.

图2 光谱图像的成像原理Fig.2 Imaging principle of spectral images

为了将(3)式离散化, 文献[12]对CCD上的每个像素进行编号, 从1到CCD像素的总个数. 假设CCD有M行J列, 则CCD的像素总个数为L=M ×J. 用矩阵A来描述校正系统, 其中的元素Atl描述了波长为l的一束单色输入光在CCD中第t个像素的流量值(不包含噪声). 校正矩阵A包含了波长校准, 光谱轨迹位置, PSF的形状及其对位置的依赖性等所有影响.A通常为稀疏矩阵, 因为在给定光纤中给定波长处的输入只会影响一定范围内的CCD像素, 而非整个CCD的所有像素. 对于1维输入光谱的向量g, 观测CCD像素流量值的向量f可以表示为:

其中n是噪声向量. (4)式也可以表示为带有索引符号的公式:

其中,ft表示编号为t的像素的流量值;gl表示波长l处的真实流量值;nt表示编号为t的像素的噪声. 向量g=(g1,g2,...,gl)T, 向量f=(f1,f2,...,ft)T. 流量提取就是在已知校正矩阵A的情况下从f复原g.

这种方法无疑突破了传统抽谱方法只适用于有限类别的可分离PSF的局限. 该方法不但能大大提高1维抽谱结果的信噪比, 而且还能保证不降低1维抽谱结果的分辨率.

但文献[12]给出的方法中矩阵A的存储量和计算量都很巨大. 对于一张记录了250条光谱,像素可达4k×4k的LAMOST图像,校正矩阵的大小可以达到(4k×250)×(4k×4k)=1.6×1013个元素. 现代的计算机无法拥有如此大的内存, 更谈不上计算了. 另外, 由于反卷积问题是一个病态问题, 其结果很容易受到噪声污染. 如果不对噪声进行抑制, 则无法抽得真实的1维目标光谱.

2.4 基于Tikhonov正则化的反卷积抽谱算法

针对LAMOST 2维光谱图像的抽谱问题, Li等[13]提出了基于Tikhonov正则化的反卷积抽谱算法(Tikhonov Deconvolution Method, TDM). 该算法通过分块的方法解决了校正矩阵存储和计算量大的问题, 并通过引入Tikhonov正则化参数抑制了噪声对抽谱结果的影响.

假设每条光纤有M行, 文献[13]中单根光纤成像(3)式离散的表示为:

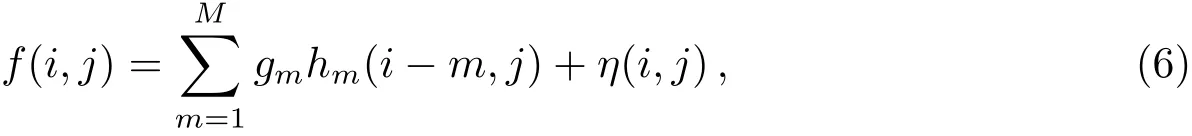
其中,f(i,j)是CCD图像第i行j列的流量值;gm是光纤在第m行的真实流量值;hm(i −m,j)表示gm对应的PSF在第i −m行j列的值;η(i,j)表示第i行j列的噪声.

若1幅2维光谱图像中有K条光纤, 那么成像公式可以描述为:

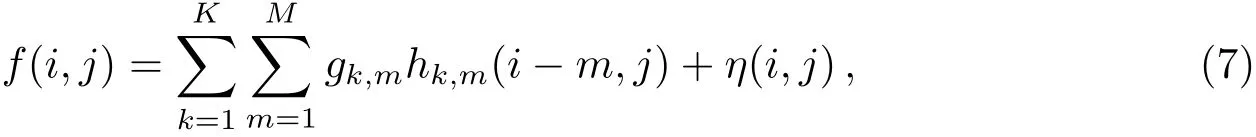
其中,gk,m是第k根光纤在第m行的真实流量值;hk,m(i −m,j)表示gk,m对应的PSF在第i −m行j列的值.

如果2维光谱图像有J列, 根据最小二乘法, 目标函数可以写为:

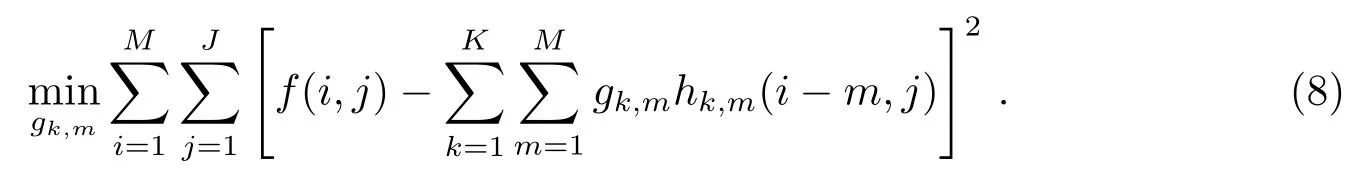
即找到一个最优解gk,m, 使得误差平方和最小.

文献[13]加入了1阶导数作为Tikhonov正则化项, 则目标函数变为:

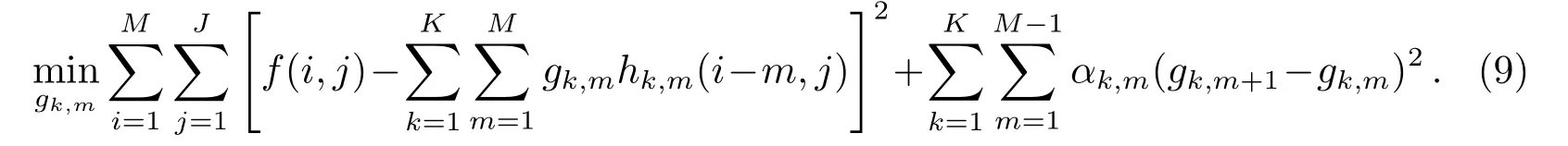
其中, 参数αk,m是正则化参数, 用来调整正则项(gk,m+1−gk,m)2的权重.

该方法引入Tikhonov正则化项, 抑制了噪声对抽谱结果的影响,提高了1维抽谱结果的信噪比. 但是, 该算法目前还没有选择合适正则化参数的有效方法. 对于Tikhonov正则化而言, 正则化参数αk,m的确定是很关键的问题. 选取不同的参数会严重影响抽谱的结果.

2.5 基于自适应Landweber迭代的反卷积抽谱算法

Li等[14]提出了一种基于自适应Landweber迭代的反卷积抽谱算法(Deconvolution Extraction Based on Adaptive Landweber Iteration, ALI). 这是一种可以自适应地给出正则化参数的反卷积抽谱算法. 该算法基于Landweber迭代算法, 通过正则化参数抑制了噪声对抽谱结果的影响, 同时给出了正则化参数的自适应选择方法.

单根光纤的离散公式(6)式的矩阵形式可以写为:

其中,H是由hm(i −m,j)组成的校正矩阵;g是由gm组成的向量,gm是向量g的第m个元素. 基于自适应Landweber迭代的公式如下:

其中,α是正则化参数, 是一个标量, 它控制收敛速率, 减少噪声对解的不确定影响;HT是校正矩阵H的转置;w为迭代次数;g(w)是对1维抽谱结果的当前估计.

该算法中自适应正则化参数的选取方法为:

其中µmax是HTH的最大特征值.

该算法同样可以提高1维抽谱结果的信噪比, 而且可以针对不同的光纤自适应地选择参数, 避免了因参数选择不当而影响1维抽谱结果.

2.6 基于Richardson-Lucy迭代的反卷积抽谱算法

Li等[15]提出了另一种基于Richardson-Lucy迭代的反卷积抽谱算法(Deconvolution Extraction Based on Richardson-Lucy Iteration, RLI). 该算法是将经典的Richardson-Lucy迭代算法经过重新推导, 应用到了LAMOST 2维光谱图像的抽谱中. 该算法同样提高了1维抽谱结果的信噪比和分辨率.

2维光谱图像成像模型的离散公式仍为(6)式, 令

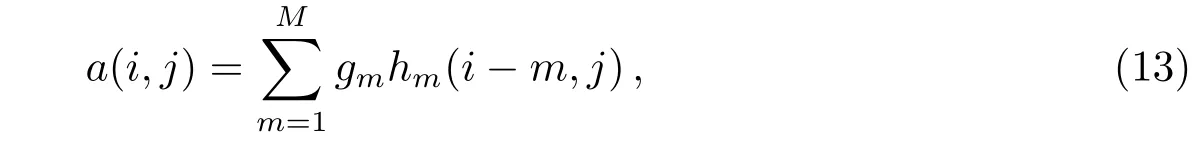
则基于Richardson-Lucy迭代的反卷积抽谱算法的迭代公式如下:

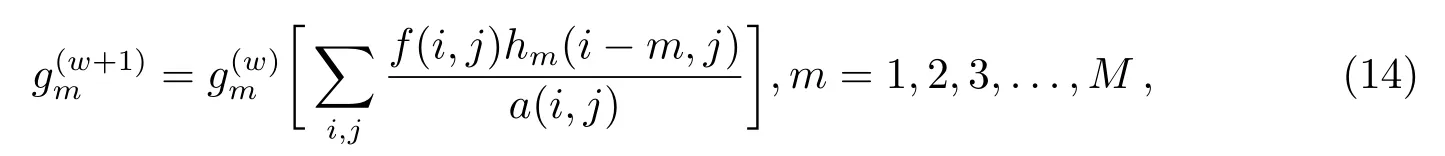
其中,f(i,j)为观测得到的2维模糊光谱图像;a(i,j)可以理解为目前估算的1维光谱g(w)m和点扩散函数hm对模糊光谱图像f(i,j)的预测, 即预测图像.

该方法最大的优点是: 比起其他的反卷积抽谱算法, 运行速度快, 并且减小了反卷积带来的振铃效应.

3 实验与分析

3.1 实验目的

本文利用LAMOST数据生成的模拟光谱图像和真实光谱图像对AEM、PFM、BDM、TDM、ALI以及RLI 6种抽谱方法的抽谱结果进行比较与分析. 具体实验内容有: (1)对LAMOST 2维模拟图像进行抽谱, 比较1维抽谱结果的信噪比以及算法的运行时间; (2)对真实的LAMOST 2维光谱进行抽谱, 比较不同算法抽谱结果的信噪比和分辨率.

3.2 实验评价指标

本实验中用到的3个评价指标有:

(1) 2维残差

光谱图像的2维残差就是对模拟生成的2维光谱图像和抽谱得到的1维结果卷积PSF得到的复原2维图像进行相减. 2维残差反映了抽谱算法对流量抽取的程度.

(2) 1维残差

1维残差是指抽谱得到的1维结果与原始输入的1维光谱之间的差值. 它可以直观反映出抽谱结果与原始输入1维光谱之间的差异.

(3) 1维抽谱结果的信噪比(Signal-to-Noise Ratios, SNR)

1维抽谱结果的SNR是用来客观地评价不同抽谱算法的1维抽谱结果的准确性. 其定义如下:

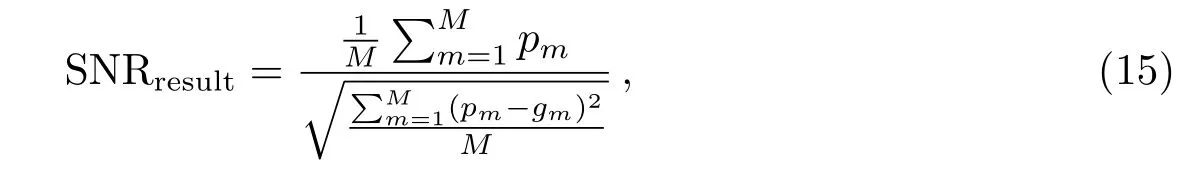
其中,pm是输入1维光谱的第m个像素的流量值.

3.3 实验数据描述

本实验使用LAMOST数据生成了抽谱的对象即模拟2维光谱图像. 首先, 从LAMOST的灯谱图像中选取了35条高信噪比的发射线作为基本的PSF, 每个PSF的尺寸大小为13×15像素. 然后对基本的PSF进行线性插值, 生成了模拟图像所需的其余所有PSF. 本实验使用孔径法对真实的LAMOST 2维光谱图像进行流量提取, 得到1条1维目标光谱, 如图3所示, 其中横坐标表示像素, 纵坐标表示流量. 该1维光谱有很明显的天光发射线, 这些发射线可以帮助评估抽谱算法的可靠性和信噪比. 模拟图像就是由这条1维目标光谱卷积所有的PSF而得到的. 模拟图像的大小为4000×15像素. 最后, 对模拟图像添加泊松噪声.

图3 生成2维光谱模拟图像的1维输入光谱Fig.3 One-dimensional input spectrum for generating the two-dimensional spectral simulation image

3.4 实验结果与分析

3.4.1 LAMOST模拟图像抽谱实验

图4显示了模拟2维图像添加的初始噪声和不同抽谱方法得到的2维残差图. 可以看出: BDM、TDM、ALI以及RLI这4种反卷积抽谱算法得到的2维残差和添加的初始噪声基本一致, 而AEM和PFM算法的2维残差在发射线周围有明显的残差.

图4 原始泊松噪声和不同抽谱算法的2维残差结果. 颜色棒以像素值为单位, 表现了不同位置处的像素值情况. (a)原始噪声, (b)–(g)分别为AEM、PFM、BDM、TDM、ALI以及RLI的2维残差.Fig.4 Original Poisson noise and two-dimensional residuals for different spectral extraction algorithms.Color bar is in units of the pixel value, which shows the pixel value at different locations. (a) is original noise; (b)–(g) are two-dimensional residuals of AEM, PFM, BDM, TDM, ALI, and RLI, respectively.

图5为不同算法的1维残差. 可以看出:

(1) BDM的1维残差最大, 因为矩阵的计算误差在计算逆矩阵的时候会不断累加. 矩阵越大, 累积误差越大. BDM反卷积算法的矩阵太大, 因此BDM计算精度很低. 同时直接反卷积受噪声影响比较严重, 无法正常地复原有噪声的图像;

(2) AEM和PFM算法的1维残差也比较明显, 因为这两种算法都没有考虑仪器的轮廓. 本文中AEM和PFM算法的抽谱结果差别不大, 因为这两种方法都是逐行进行光通量提取的, 即在每一个给定行估计真实的光通量. 再加上CCD仪器本身的噪声很小, 因此,这两种方法在任意行的差值只在泊松噪声水平;

(3) TDM、ALI和RLI这3种正则化的反卷积抽谱方法得到的1维抽谱结果最接近真实的1维输入光谱. 因为这3种方法既消除了仪器的误差, 又抑制了噪声对1维抽谱结果的影响. 但是, TDM抽谱方法的参数选择会影响1维抽谱结果[14]. 本实验选择了TDM方法的最佳参数, 得到了该方法下的最佳1维抽谱结果.

图5 不同抽谱算法的1维残差. (a)–(f)分别为AEM、PFM、BDM、TDM、ALI以及RLI的1维残差.Fig.5 One-dimensional residuals of different spectral algorithms. (a)–(f) are one-dimensional residuals of AEM, PFM, BDM, TDM, ALI, and RLI, respectively.

表1记录了不同抽谱算法的运行时间和1维抽谱结果的信噪比. 信噪比计算公式如(15)式. 从表1可以看出:

(1) AEM的抽谱时间最短, BDM的抽谱时间最长. 因为BDM方法的校正矩阵太大,存储和运算都花费了大量的时间和内存空间;

(2) TDM、ALI和RLI这3种正则化的反卷积抽谱方法的信噪比处于相似水平, 但是RLI运行最快. TDM在求逆矩阵的过程中花费了不少时间.

从模拟图像的抽谱实验可以看出: 正则化的反卷积抽谱方法得到的1维抽谱结果比传统的孔径法和轮廓拟合法在信噪比方面有很大的提高. 传统的孔径法在抽谱时间方面有很大的优势. 直接反卷积方法应用在有噪声的2维光谱图像抽谱中无法得到正常的1维抽谱结果.

表1 不同抽谱算法的运行时间和1维结果的信噪比Table 1 Running time and SNR of resulting one-dimensional spectra of different extraction algorithms

3.4.2 真实LAMOST光谱图像抽谱实验

本实验采用不同的抽谱算法对真实的LAMOST 2维光谱图像进行抽谱实验. 鉴于模拟实验中, 孔径法和轮廓拟合法的结果相差不大, 而直接反卷积方法又无法在有噪声的光谱图像中提取到正常的1维抽谱结果, 本实验仅采用了AEM、TDM、ALI以及RLI作比较. 为了验证抽谱结果的信噪比和分辨率, 采用文献[16]中给出的天光发射线卷积了1个高斯轮廓, 合成了1条1维的天光光谱. 图6为1维抽谱结果的局部图, 从上到下分别是AEM、TDM、ALI、RLI的1维抽谱结果以及文献[16]合成的1维天光光谱. 为了便于比较, 所有的光谱在纵坐标上都进行了平移.

图6 LAMOST真实光谱图像的1维抽谱结果(局部). 从上到下分别代表AEM、TDM、ALI、RLI的1维抽谱结果以及文献[16]合成的1维天光光谱.Fig.6 Resulting one-dimensional spectra (local) of real LAMOST spectrum images. From top to bottom,the lines represent AEM, TDM, ALI, RLI and one-dimensional skylight spectrum synthesized in Ref. [16],respectively.

从图6可以看出:

(1)在波长为8290 ˚A和8386 ˚A处, AEM的1维抽谱结果受噪声污染更严重. 说明正则化的反卷积抽谱算法得到的1维光谱在信噪比方面优于传统孔径法得到的1维抽谱结果;

(2) TDM、ALI和RLI抽谱结果的轮廓比AEM结果的1维轮廓窄. 说明正则化的反卷积抽谱算法得到的1维光谱在分辨率方面优于传统孔径法得到的抽谱结果;

(3) TDM、ALI和RLI得到的1维结果的发射线部分更加对称. 说明正则化的反卷积抽谱方法确实可以校正CCD中的PSF形变;

(4)从虚线标明的地方可以看出, TDM、ALI和RLI都会出现一定程度的伪特征, 这是振铃效应导致的. 其中, RLI的振铃效应的幅度小于TDM和ALI.

4 结论

本文针对LAMOST 2维光谱图像数据, 对6种抽谱算法从理论和实验两方面进行了分析与比较. 通过研究可以得出以下结论:

(1)从1维抽谱结果的精确度而言, 基于Tikhonov正则化的反卷积抽谱算法, 基于自适应Landweber迭代的反卷积抽谱算法和基于Richardson-Lucy迭代的反卷积抽谱算法提高了LAMOST 2维光谱图像的1维抽谱结果的信噪比和分辨率;

(2)从抽谱效率而言, 孔径法是最高的, 目前它仍是LAMOST的pipeline所采用的抽谱方法. 基于Richardson-Lucy迭代的反卷积抽谱算法是3种正则化的反卷积抽谱算法中最快的.

通过分析和比较各种算法, 根据各自的优缺点提出了下一步研究的展望:

(1)正则化的反卷积抽谱算法都可以方便地转化为并行算法. 对于多处理器计算机,可以使用1个处理器1次计算1根光纤. 这样可以大大提高多目标光纤光谱图像的抽谱效率;

(2)可以将孔径法和正则化的反卷积方法相结合. 为了节省计算时间, 可以首先采用孔径法抽取目标天体的1维光谱, 然后再用正则化的反卷积方法从该1维光谱中再次抽取, 最后得到的1维光谱会具有更高的分辨率和信噪比. 相比于直接从CCD 2维光谱中反卷积抽取1维光谱的做法, 该方法可以大大节省抽谱时间.