多星中天时角法精密测定天文方位角∗

刘新江 郑 勇 李崇辉

(1 战略支援部队信息工程大学地理空间信息学院郑州450001)

(2 61365部队天津300140)

(3 地理信息工程国家重点实验室西安710054)

(4 西安测绘研究所西安710054)

1 引言

天文方位角测量以大地水准面和铅垂线为参考基准, 目前在可直接作为方位基准应用于工程测量的地面绝对定向方法中精度最高[1–2]. 在已知坐标的测站上, 观测任意一颗识别天体的水平角和天顶距(天顶距法), 或者观测水平角的同时记录测瞬时刻(时角法), 都可以进行天文定向[3–5]. 天顶距法受大气垂直折光影响大, 精度偏低, 高等级天文方位角测量采用时角法. 北极星亮度高, 赤纬接近90◦, 视运动幅度很小, 因此, 北半球中纬度地区多采用北极星任意时角法测量天文方位角[6–9]. 但由于北极星并不正好位于北天极, 测量天文方位角之前必须已知测站的精确天文经纬度. 此外, 低纬度和南半球地区根本无法观测北极星. 有学者提出在低纬度地区采用子午星对法测量天文方位角, 每个星对为子午圈上南、北两颗赤纬余弦与天顶距正弦之比相等或相近的恒星. 此方法测量精度较高, 但由于受配对条件限制, 在中、高纬度地区可观测星对少, 等星时间较长[10]. 本文在分析中天星测定方位角的主要误差后提出多星中天时角法, 只需已知测站的概略坐标即可, 省却了复杂而精密的天文定位观测; 不需要选星配对, 视域内的全部中天天体均可用于观测; 针对测站经度误差和计时误差的影响, 建立回归模型精密确定出测站至某一地面目标的天文方位角.

2 时角法测定天文方位角

在地平坐标系中, 地平经度也称方位角, 指测站子午面与天体垂直面之间的夹角. 在大地天文学中, 天文方位角特指测站所在子午面与通过地面上另一点(目标)的垂直面之间的夹角, 自正北方向起顺时针量算, 值域范围[0◦, 360◦). 因此, 天文方位角可以分解为某一天体与测站子午面间的夹角(即天体方位角)和天体与地面目标间的水平夹角, 概略定位定向后重复观测地面目标和选定天体. 天体为运动目标, 其测量精度决定了天文方位角的精度水平.

2.1 时角法测定天体方位角误差分析

时角法测定天体方位角A的基本公式:

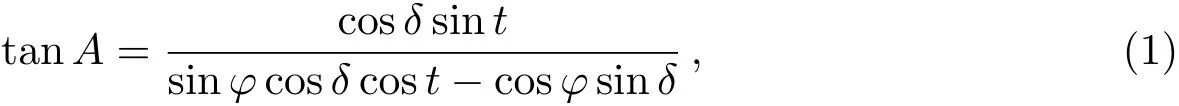
式中,δ为天体赤纬,t为天体时角,φ为测站纬度.

不考虑恒星星表误差, 仅考虑本地纬度误差和时角测量误差, 误差方程为:

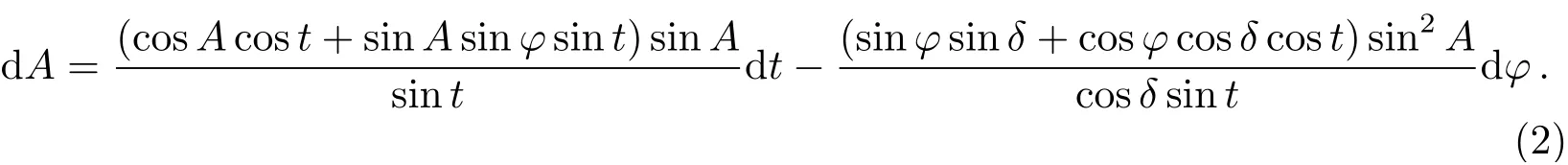
用q表示星位角,z表示天顶距, ∆λ和∆φ分别表示测站经度误差和纬度误差, ∆T表示计时误差, 时角误差∆t=∆T+∆λ, 上式简化后得

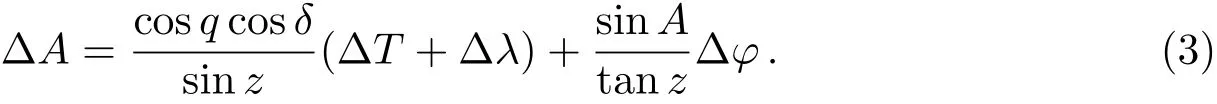
当A=0◦或180◦时, 测站纬度误差对定向没有影响; 当δ=90◦或q=90◦时, 测站经度误差和计时误差对定向没有影响.

2.2 北极星任意时角法

北极星任意时角法只观测北极星, 忽略时角差异, 取各测回测量值的均值作为最终成果. 由于北极星并不恰好在北天极上, 其赤纬约为89◦16′, 如果测站位置误差和计时误差较大, 仍会给定向带来较大的影响. 图1给出了北纬20◦、45◦和70◦的测站上定向误差随时角的变化(令测站经度误差和计时误差之和为5′′, 测站纬度误差为5′′). 可以看出: (1)纬度越高, 定向误差越大. 在低、中、高纬度测站上, 定向误差从±0.1′′以内到接近±0.2′′, 最大可达±0.6′′; (2)测站位置误差和计时误差对定向精度的影响随时角变化,为了避免各测回都在同一时角观测, 造成所有结果均偏大或偏小一定数值成为系统误差, 规范中要求在不同时间段(傍晚和夜晚)观测[11].

天文测量目前多采用电子经纬仪加导航卫星授时技术[8–9,12–13], 可以很方便地获得较为精确的测站大地经纬度. 如果没有精确的本地垂线偏差模型, 测站位置误差会达数角秒至十几角秒, 必然引起较大的定向误差. 因此, 该方法测量天文方位角之前需精密测定测站的天文经纬度.

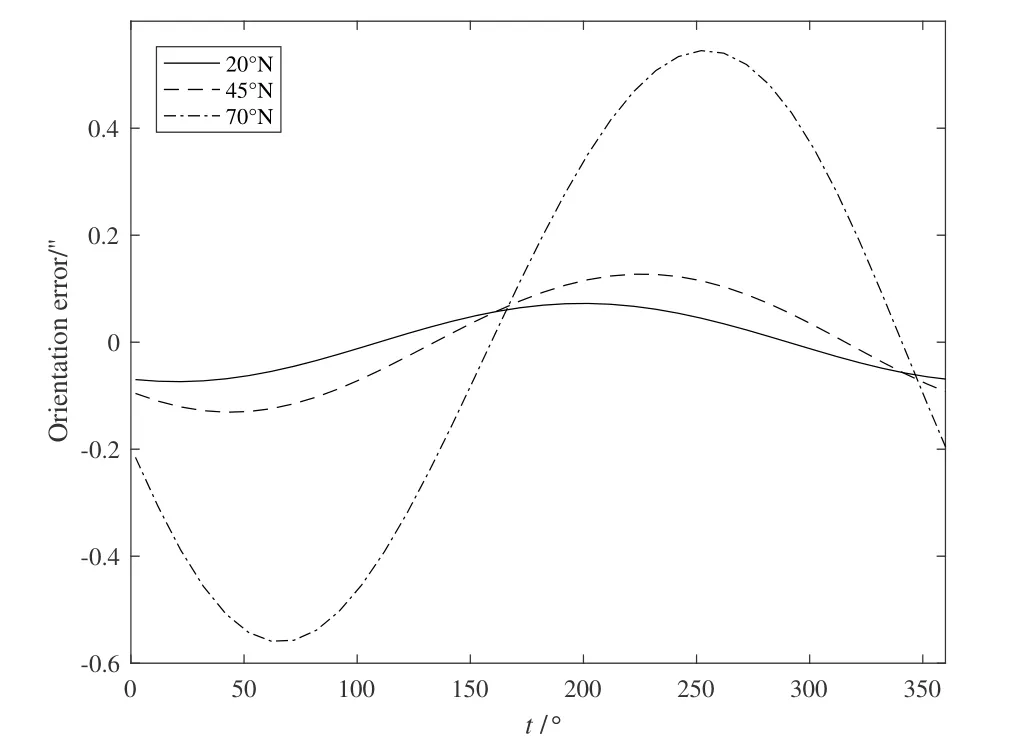
图1 测站位置误差和计时误差对北极星定向的影响Fig.1 Influence of station position error and timing error on the orientation by Polaris

2.3 单星中天时角法

天体经过测站所在子午圈称作中天. 每个天体1 d中两次经过子午圈, 离天顶较近的一点称作上中天, 离天顶较远的一点称作下中天. 若天体在天顶以北过中天, 称为北星;反之, 称为南星. 显然, 南北星的赤纬和天顶距与本地纬度满足简单的线性关系, 以南点为起始方向, 南星的方位角AS和北星的方位角AN分别近似为0◦和180◦. 实际测量中很难保证恰在中天时刻观测, 只能做到t ≈0. (1)式简化为[14]:

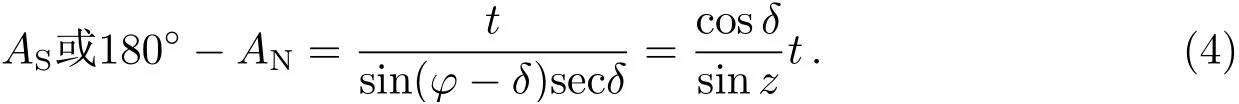
本方法计算简单, 但测站经度误差和计时误差全部包含在时角误差内, 天体赤纬越大, 天顶距越大, cosδ/sinz的数值越小, 时角误差引起的天体方位角误差就越小. 因此,应尽可能观测靠近天极的中天天体.

2.4 子午星对法

采用中天时角法定向, sinA ≈0, cosq=±1, (3)式简化为

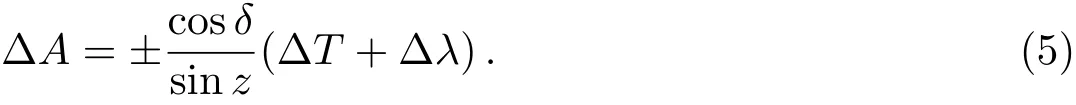
如果在同一测站上连续观测南、北两颗中天天体, 组成一个子午星对[10], 方位角误差取均值得

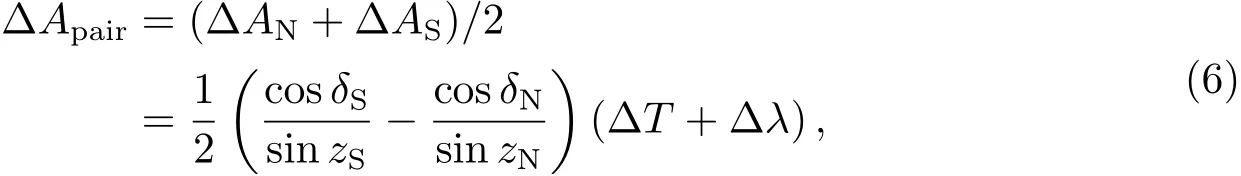
式中, 下标N和S分别表示北星和南星.

显然, 最佳配对条件为:

此时, (∆T+∆λ)对天体方位角没有影响.

图2为在北半球不同纬度测站上, 南北星天顶距在[20◦, 70◦]区间内的cosδ/sinz值.为了方便对比, 南星的天顶距用负值表示. 南半球同理. 可以看出, 在20◦N测站上, 南北两星的cosδ/sinz值重合区间较大; 在45◦N测站上, 南北两星的cosδ/sinz值重合区间很小, 但上中天北星和下中天北星有一段重合区间; 在70◦N测站上, 不再有重合区间. 因此, 子午星对法主要适用于低纬度地区.

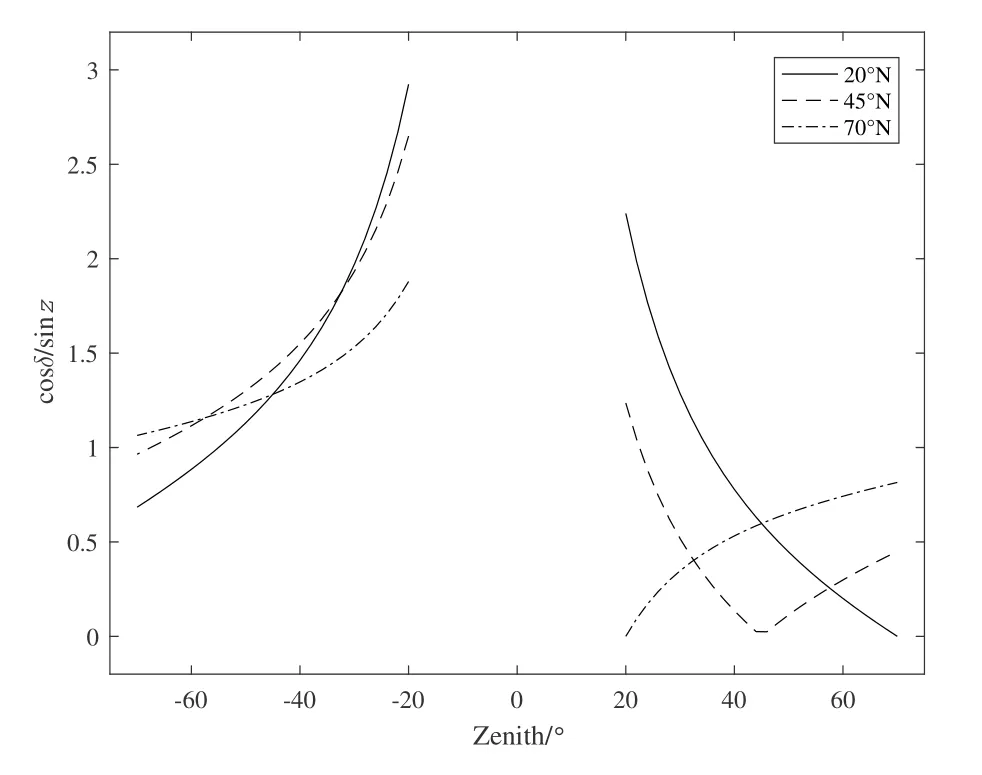
图2 南北星cos δ/sin z在北半球不同纬度测站上随天顶距的变化Fig.2 cos δ/sin z variation of south and north stars according to the zenith distance at different latitudes in the northern hemisphere

由于自然天体在天球上的分布不均匀, 即使在低纬度地区也很难在短时间内连续观测到严格符合最佳配对条件的两颗子午星. 为了观测到足够数量的星对, 只能放宽限制条件, 将(7)式左侧数值限制在设定阈值m以内, 一个子午星对测站经度误差和计时误差对计算方位角引起的最大误差为(∆T+∆λ)m/2.

3 多星中天时角法

若已知测站经度误差和计时误差之和(∆T+∆λ), 则观测任意一颗中天天体的方位角及其与地面目标之间的水平夹角, 都可以获得准确的测站至地面目标的天文方位角.本文提出的多星中天时角法, 就是观测多颗中天天体和地面目标后通过回归模型估计出(∆T+∆λ)的方法.

3.1 分析变量关系

通过观测某颗中天天体及其与地面目标的水平夹角, 获得的测站至地面目标的天文方位角Ai中(下标i代表第i次观测, 下同), 包含由于测站经度误差和计时误差给天体方位角带来的系统误差∆Ai和水平夹角观测中的偶然偶差εi,

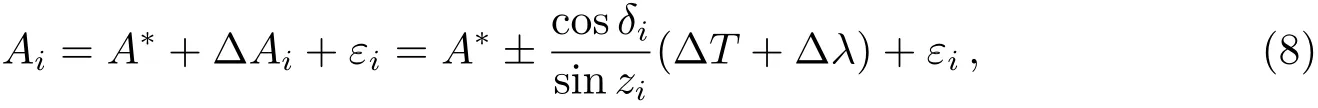
其中A∗表示天文方位角的最佳拟合值,εi为零均值随机误差.

在观测时段内, ∆λ为常数, ∆T与时钟的精度相关, 假设初始比时误差为a, 初始频率偏差为b, 频率漂移率为c, 则∆T与观测时长l之间的关系为

∆λ、a、bl、cl2的单位均转换为角秒, 代入(8)式, 令±(cosδi/sinzi)=pi, 得

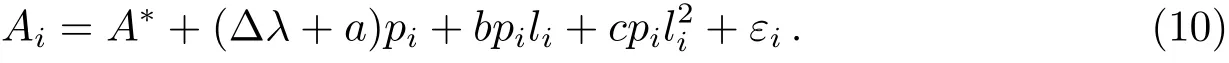
假设独立观测了n组数据,令回归变量为x=(x1,x2,x3)T=[(p1,...,pn),(p1l1,...,pnln),(p1l21,...,pnl2n)]T, 响应变量为y=(A1,A2,...,An)T, 回归参数β=(β0,β1,β2,β3)T=[A∗,(∆λ+a),b,c]T显著, 则可以建立n个回归方程:

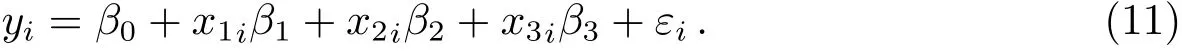
3.2 确定回归模型

精密天文测量中采用的时钟精度和稳定性都很高, (10)式中的a、b、c数值很小, 采用大地经度作为近似天文经度时∆λ在几角秒到十几角秒量级, 通过仿真数据对∆λ+a、b、c进行显著性检验.

假设在4 h内等间隔观测200组数据,l为等差数列,p值在[−2,2]区间内均匀分布,∆λ+a=5,b=0.001,c=0.001, 随机误差服从正态分布ε∼N(0,32)[16],A∗= 0. 变量p、pl、pl2、A之间的简单相关系数矩阵为[17]

进一步计算变量p、pl、pl2、A之间的偏相关系数(固定其余变量的影响)矩阵为

从简单相关系数来看, 回归变量p、pl、pl2与响应变量A的相关性均较强, 但回归变量之间也存在着很强的相关性. 偏相关系数矩阵中则只有p与A的相关性较强,pl和pl2对回归的贡献很小. 令b、c分别取相同值0.001、0.01和0.1, 进行多元回归和一元回归分析, 每种情况模拟100次. 表1列出了拟合参数的均值(括号内为参数均值标准差), 可以看出, 由于多元回归变量间存在较强的复共线性, 拟合得到的参数标准差较大. 一元回归与多元回归拟合得到的A∗几乎没有差别,b、c的数值一般远小于0.01 (目前的天文大地测量系统多使用计算机守时, 钟速中误差小于0.1 mas·h−1, 几天内钟速变化小于5 mas·h−1[8]), 此时∆λ+a的差异也很小. 因此, 一元回归模型更为适用.

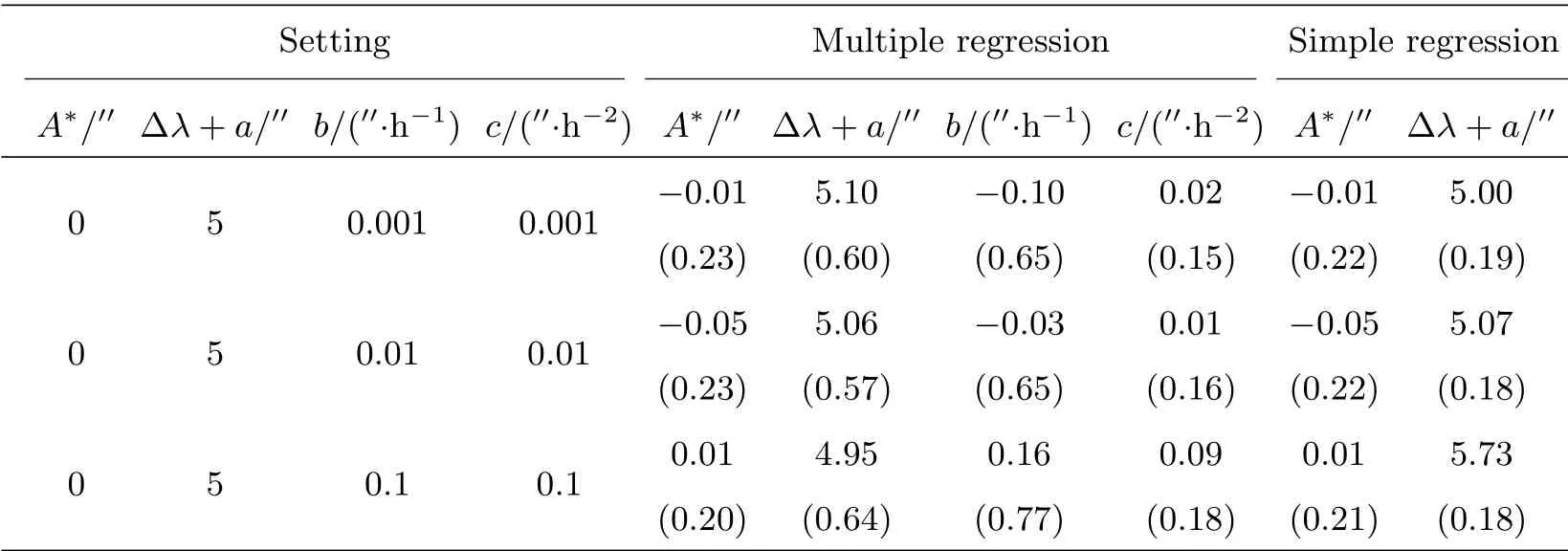
表1 多元回归和一元回归参数比较Table 1 Parameter comparison of multivariate and univariate regressions

3.3 确定样本数量

从b、c取值0.001的仿真数据中, 分别随机选取不同数量的样本, 进行一元线性回归.当样本数达到30以上时, 回归参数∆λ+a与设定值的差值均小于0.05′′. 图3中每个数据点表示不同样本数量计算得到的拟合方位角A∗的标准差, 可以看出随着样本数量的增大标准差逐渐减小. 设σA∗为拟合方位角标准差,k为样本数量, 由散点图得到拟合曲线:

如果所需的成果精度为σA∗, 观测样本数量k的参考值为:

4 实验结果分析

在20◦N附近某地区选取相距2–3 km的5个地面点, 进行了7个方向的方位角测定. 采用Y/JGT-01型天文测量系统, 其中观测仪器为TS30全站仪, GPS导航卫星授时, 笔记本电脑守时, 星表系统采用依巴谷星表.

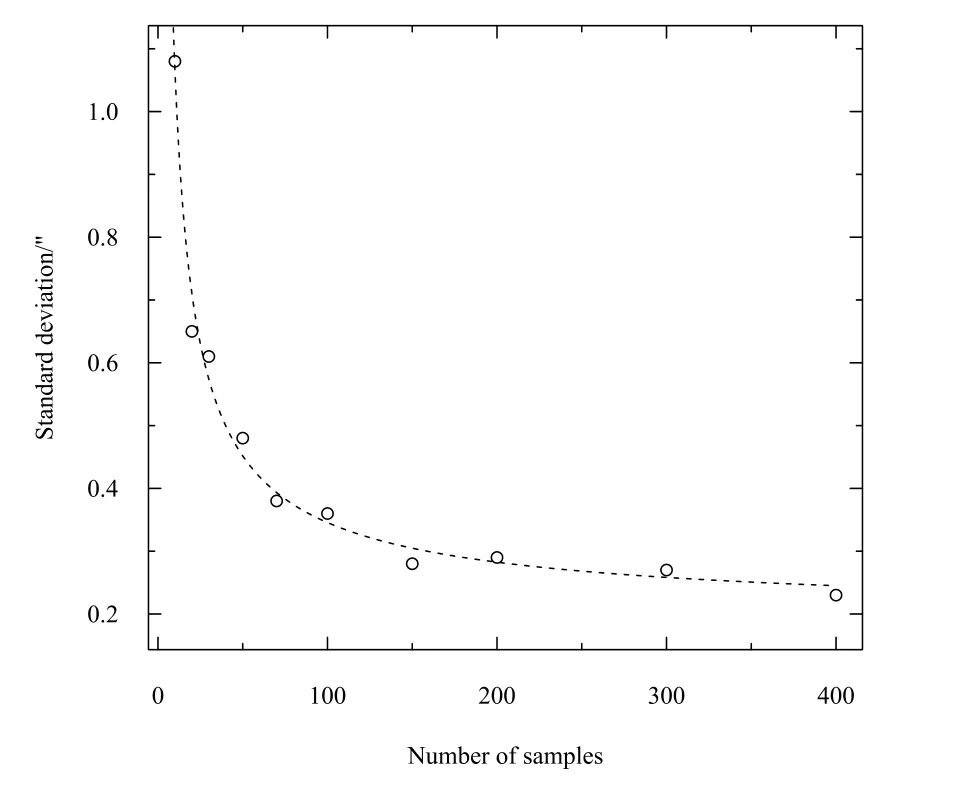
图3 拟合方位角标准差随样本数量的变化Fig.3 The standard deviation of fitting azimuth varies with the number of samples

首先采用北极星任意时角法按照一等观测纲要施测[11], 获取7个方向的一等天文方位角成果, 作为中天时角法测量结果的评定基准. 然后在各测站上一南一北交替观测中天星, 为了获得±0.3′′精度水平的成果, 按照(13)式计算得出应观测160组以上的数据(由于天气原因, 5–2方向未能观测到足够的数据). 表2列出了每个方向观测的中天星总数和匹配得到的子午星对数, 每颗星连续观测6次, 子午星对法的星对匹配阈值设定为±0.3((7)式左侧计算值). 分别采用单星中天时角法、子午星对法和多星中天时角法, 选择相应的数据进行处理.

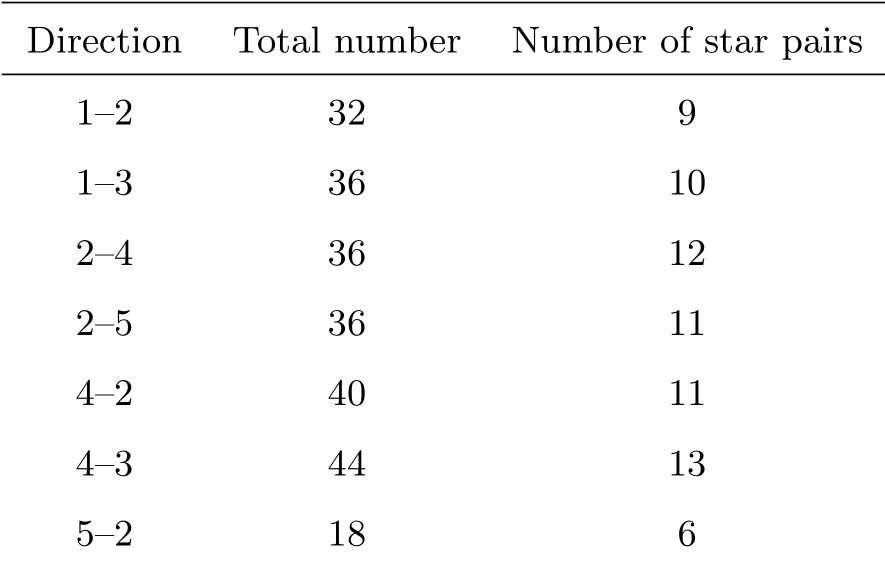
表2 各方向测星数统计Table 2 Statistics of stars in each direction

表3为多星中天时角法回归变量和响应变量的相关系数R及在0.01显著性水平下的检验临界值R0.99(n −2)=表示0.01显著性水平下自由度为(1,n−2)的F检验临界值. 可以看出,所有方向上的R均远大于R0.99(n−2),表明线性回归效果极显著.

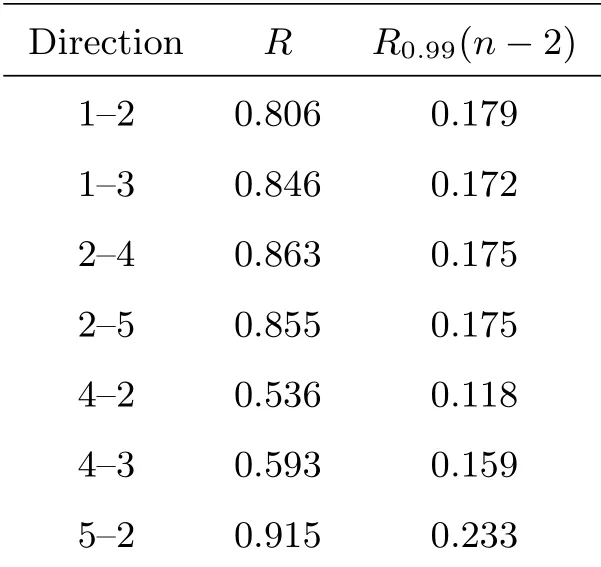
表3 多星中天时角法相关系数检验Table 3 Correlation coefficient test of multi-star meridian hour angle method

3种方法计算天文方位角的标准差见图4. 可以看出, 多星中天时角法的精度最高,标准差均小于0.4′′. 子午星对法次之, 单星中天时角法的精度最差. 5–2方向由于观测数据量小, 精度明显低于其他方向.

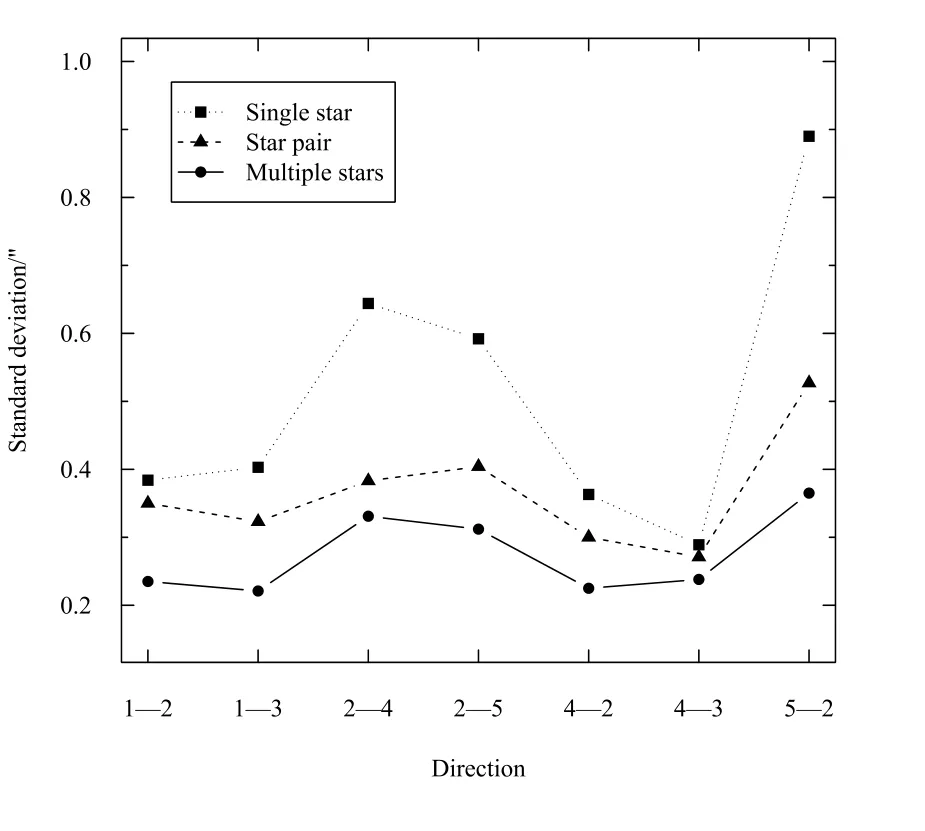
图4 3种方法计算结果标准差比较Fig.4 Standard deviation comparison of three methods

图5为3种方法计算结果与北极星任意时角法获得的一等成果的差值. 可以看出, 单星中天时角法的计算结果明显大于基准值, 这是由于观测中天星的cosqcosδ/sinz值正负不对称造成的. 子午星对法的计算结果在观测数据量较少时(5–2方向)出现了较大的偏差. 多星中天时角法的计算结果最为稳定, 与基准值的差值均小于0.5′′, 但全部为正值, 可能是由于自变量区间正负不对称造成的. 由图2可以看出, 测站位于20◦N时, 南北两颗等高星的cosδ/sinz不等, 导致自变量正值区间的数值大于负值区间的数值. 但在没有粗差的情况下, 对回归参数的影响应该很小, 这一点还有待通过更多的不同纬度测站上的实验数据对回归方法作进一步研究.

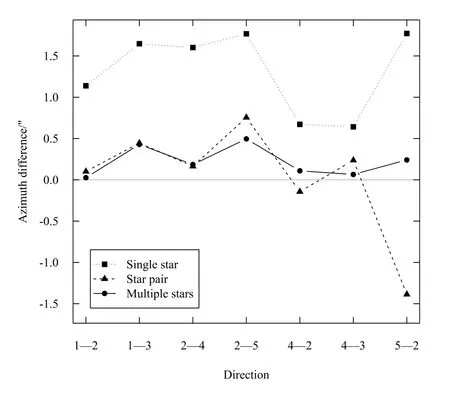
图5 3种方法计算结果与一等成果的差值Fig.5 The results of three methods comparing with the first-order results

《大地天文测量规范》中规定: 一等天文方位角采用北极星任意时角法观测18个测回, 每个测回照准北极星24次, 成果中误差限差为±0.5′′. 本实验中前6个方向的观测量仅为规范要求的一半左右(5–2方向仅为1/4), 从成果标准差和与一等成果的差值两项指标来看, 多星中天时角法计算结果已经达到一等天文方位角精度要求.

5 结论

多星中天时角法通过回归模型解算测站至地面目标的天文方位角, 理论上可以完全消除测站经度误差和计时误差的影响, 观测前不需再对测站进行精密天文定位, 可直接将通过导航卫星测量得到的大地经纬度作为概略天文经纬度使用. 与北极星任意时角法测定一等天文方位角相比, 不需在多个时间段内观测, 即使减少一半观测量, 仍能获得精度相当的成果. 与子午星对法相比, 观测星的中天位置没有限制, 增加了可观测星数量,并且不需要制作专用星表. 回归分析具有探测粗差的功能, 因此多星中天时角法具有较强的鲁棒性. 北极星任意时角法只能应用于北半球中纬度地区, 子午星对法主要适用于低纬度地区, 多星中天时角法将精密天文定向测量的工作范围扩展至全球任意地区.

致谢感谢信息工程大学杜兰教授仔细审阅了论文初稿. 感谢审稿人提出的宝贵建议.