波形钢腹板−钢底板−混凝土顶板组合箱梁的有效分布宽度研究

马驰，刘世忠，陈权，王君楼

波形钢腹板−钢底板−混凝土顶板组合箱梁的有效分布宽度研究

马驰，刘世忠，陈权，王君楼

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

考虑混凝土顶板和钢底板不同的模量，结合变分法推导波形钢腹板-钢底板-混凝土顶板(简称CSWSB)组合箱梁剪力滞效应的控制微分方程组和边界条件，建立CSWSB简支组合箱梁跨中集中荷载、均布荷载作用下剪力滞系数和有效分布宽度的计算公式，采用模型试验梁对2种荷载工况下单箱单室组合箱梁的剪力滞效应和有效分布宽度进行分析。研究结果表明：简支组合箱梁在集中荷载和均布荷载作用下剪力滞系数表达式正确，集中荷载作用下的剪力滞效应比均布荷载作用下的剪力滞效应明显，上翼缘板的剪力滞效应比下翼缘板的剪力滞效应明显；根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》计算CSWSB组合箱梁翼板有效分布宽度时，与理论计算局部差值达到了10%，富余量较小；与《钢-混凝土组合桥梁设计规范》计算CSWSB组合箱梁翼板有效分布宽度对比，整体差值率偏大，设计中应给予重视。

波形钢腹板；组合箱梁；变分法；剪力滞系数；有效分布宽度

钢腹板−钢底板−混凝土顶板(简称CSWSB)组合箱梁形式相比传统波形钢腹板(简称CSW)组合箱梁具有以下优点：钢材具有更好的抗拉性能，底板尺寸大大降低，进一步减轻了梁体的自重；受力更为合理，构造更为简单；跨内梁体底板受拉，钢材的抗拉性能可以得到充分发挥，可免除跨中正弯矩区域的预应力配筋，同时避免了底板混凝土收缩徐变、体内预应力布置等问题；中支点附近钢底板受压，可设置剪力键局部浇筑混凝土底板与钢板组成组合结构板，既可以增大抗压截面面积，同时混凝土对钢板又形成约束，有效避免钢底板的失稳问题；截面整体性更好，避免了波形钢腹板与混凝土底板剪力键连接的薄弱环节，施工质量更易保证，检修维护更为方便；整个结构的抗震性能更好，设计中可以减少桥梁墩台结构的截面面积，使桥墩桥台更为轻质、薄壁。在波形钢腹板−钢底板−混凝土顶板组合箱梁弯曲变形时，混凝土顶板和钢底板由于剪切变形的影响，从而不在服从弯曲初等梁理论变形的平截面假定，即剪力滞效应[1]。吴文清等[2]通过模型试验，得出了传统波形钢腹板组合箱梁剪力滞效应的分布规律和理论计算方法，为CSW组合箱梁剪力滞系数的计算提供了理论依据。李立峰等[3−4]得出不同载荷作用下CSW组合箱梁剪力滞效应计算表达式，并探讨了该类型箱梁波高区混凝土的计算取值问题。周茂定等[5]结合薄壁箱梁比拟杆法的计算原理，推导出对CSW组合箱梁采用三杆比拟叠加法求解剪力滞系数的计算公式。陈水生等[6]在重新定义CSW组合箱梁的剪滞翘曲位移函数的基础上，得出了单箱多室CSW组合箱梁的解析解。卫星等[7]根据7种结构几何参数变化，讨论了CSW PC 组合箱梁与预应力混凝土箱梁的剪力滞效应的分布情况。石聪等[8−9]采用换算截面法对单箱单室和双箱单室CSWSB组合箱梁的剪力滞效应进行了综合分析。虽然各位学者提出了一些剪力滞效应的理论计算方法，但是计算比较复杂且通用性不强。根据我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[10]给出的普通钢筋混凝土结构翼缘有效分布宽度考虑剪力滞效应的计算公式，部分学者在有效分布宽度方面作了研究，程坤[11]对大跨度变截面CSW组合连续箱梁翼缘有效分布宽度计算进行了分析。赵品等[12]通过试验模型，研究了CSW组合箱梁桥面板有效分布宽度规律。但是对CSWSB组合箱梁的有效分布宽度尚未见学者进行研究。本文以CSWSB组合箱梁为研究对象，考虑混凝土顶板和钢底板不同的模量，结合变分法推导了该类型组合箱梁剪力滞效应的控制微分方程组和边界条件，建立了CSWSB简支组合箱梁剪力滞系数和有效分布宽度的计算公式，并将理论计算值与实测值和有限元值进行对比分析，验证了理论的正确性。并根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》计算的CSWSB组合箱梁翼板有效分布宽度与理论计算值进行了对比分析。

1 微分方程的建立及求解

假定组合钢箱和混凝土板符合“拟平截面假定”，波形钢腹板只考虑，钢梁底板和混凝土顶板只考虑和γ。该组合箱梁中各板件的纵向位移(,,)由初等梁理论计算的弯曲纵向位移u(,)和剪力滞纵向翘曲位移u(,,)组成，即

式中：(,)为适用于该组合箱梁桥的剪力滞翘曲位移函数。CSWSB组合梁截面见图1，波形钢腹板构造见图2。

图1 CSWSB组合箱梁截面示意图

图2 波形钢腹板几何构造图

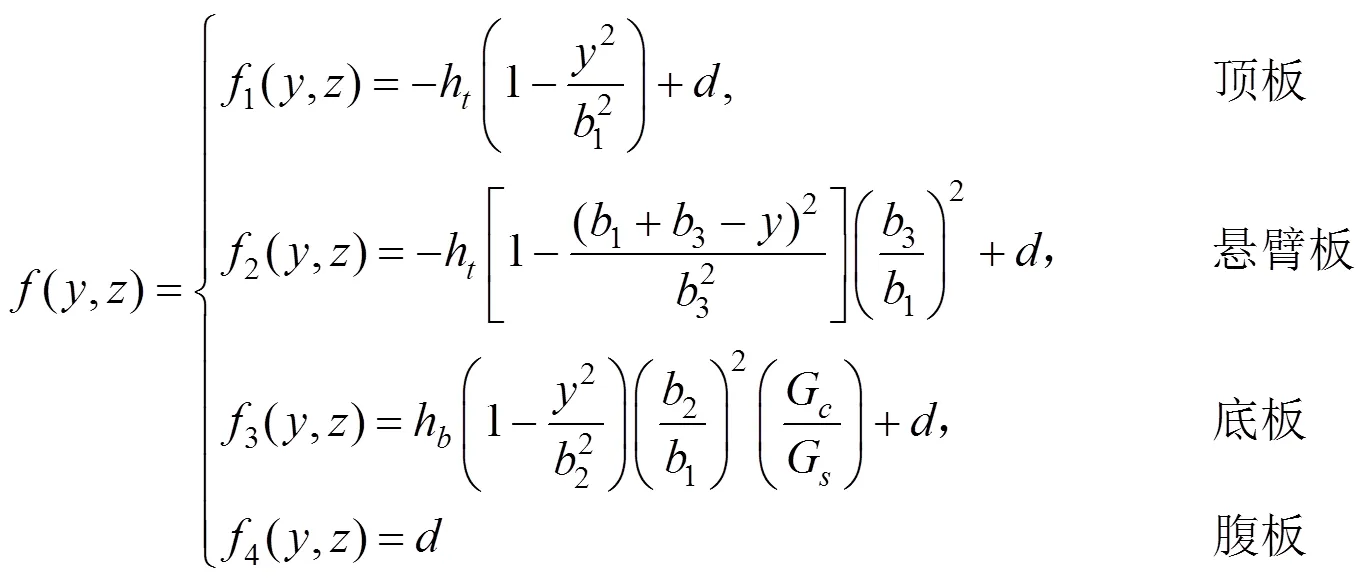
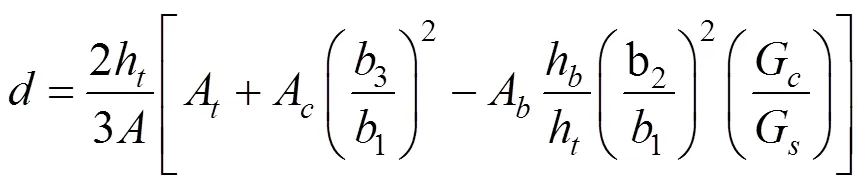
Samanta在文献[13]中给出波形钢腹板的剪切模量G应按下式进行修正计算：

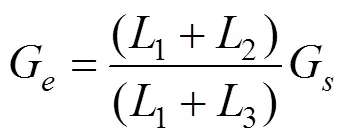
式中：1，2和3表示几何尺寸如图2所示。

CSWSB组合箱梁体系的总势能为：

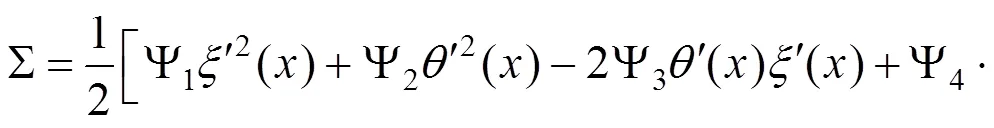
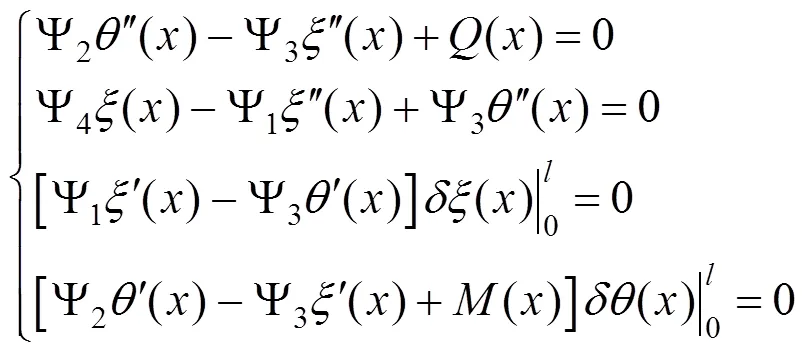
得到剪力滞微分方程为：

微分方程解的一般表达式：

为与剪力()分布有关的特解，1和2由边界条件确定。

考虑剪力滞效应的弯曲正应力为：

式中：计算上翼缘板剪力滞效应的弯曲正应力时E取E，计算下翼缘板剪力滞效应的弯曲正应力时E取E，h为翼缘板的坐标。

CSWSB组合箱梁剪力滞系数为：

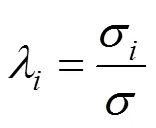
式中：为初等梁理论计算的CSWSB组合箱梁的纵向正应力。

CSWSB组合箱梁有效分布宽度为：真实应力曲线所包围的面积与真实峰值应力max(为阴影矩形面积的高)的比值，即为翼缘的有效分布宽度(阴影矩形面积的边长)。

式中：为CSWSB组合箱梁翼板的有效分布宽度；为组合箱梁翼板的实际宽度；为组合箱梁翼缘的实际厚度；为组合箱梁翼缘的实际正应力；max为组合箱梁翼缘的实际正应力峰值。

2 CSWSB简支组合箱梁在不同荷载工况的剪力滞效应

2.1 简支梁集中荷载工况的剪力滞效应

CSWSB简支组合箱梁的集中荷载工况如图3所示。

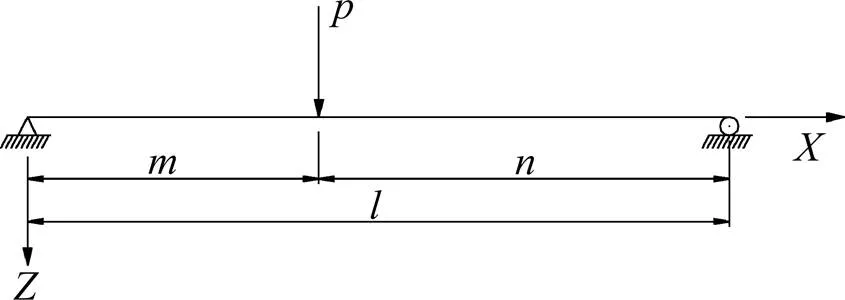
图3 CSWSB简支组合箱梁集中荷载工况示意图

以上2种情况分别代入式(7)，得

边界条件：

根据以上4个边界条件，代入4个方程并求解4个方程得：

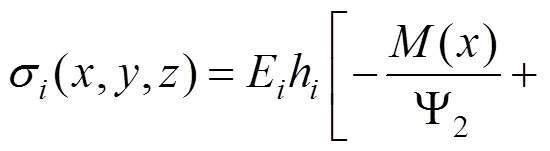
2.2 简支梁均布荷载工况的剪力滞效应

CSWSB简支组合箱梁在均布荷载工况的示意图如图4所示。

图4 CSWSB简支组合箱梁均布荷载工况示意图

弯矩与剪力函数为：

代入式(7)求解得，

考虑剪力滞效应的弯曲正应力为：

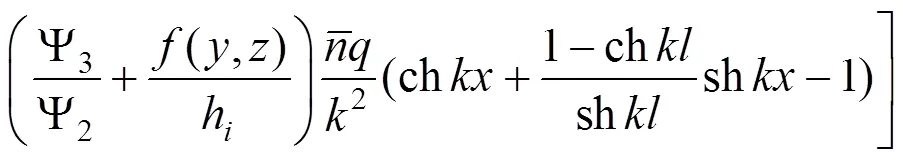
代入式(10)得CSWSB组合箱梁跨中截面剪力滞系数为：

3 CSWSB组合箱梁剪力滞系数分析的算例

3.1 单箱单室简支梁的剪力滞系数分析

试验梁的横截面尺寸是参照交规院设计的40 m跨径的CSWSB组合箱梁桥的截面尺寸设计，并按照1:5的比例进行缩小。单箱单室CSWSB模型试验梁横截面如图5所示，试验梁混凝土顶板采用C50细石混凝土，波形钢腹板和钢底板均用Q235钢板制作，Q235钢材的s为206 GPa，为0.3，普通钢筋采用φ6的一级钢筋。单箱单室CSWSB简支组合箱梁，计算跨径为8 m，共设置7道横隔板，单箱单室CSWSB模型试验梁半顶板半底板平面图(如图6所示)。单箱单室CSWSB连续组合箱梁均布荷载加载图(如图7所示)。

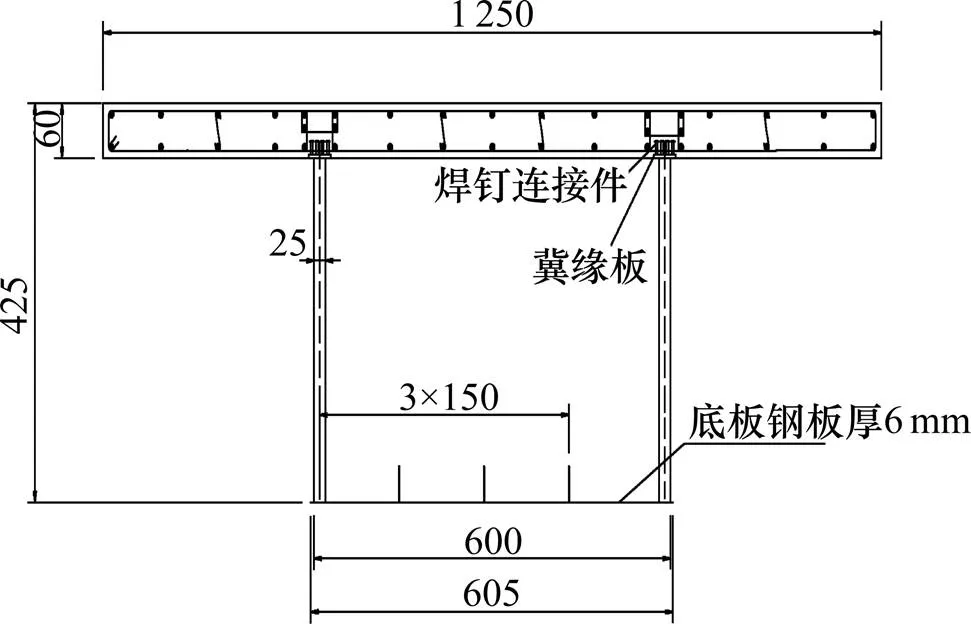
单位：mm

采用软件ANSYS 15.0版对CSWSB组合箱梁建立有限元模型，组合箱梁混凝土顶板采用实体单元SOLID45来模拟，波形钢腹板、钢底板、纵肋及横隔板均采用板壳单元SHELL63来模拟。单箱单室CSWSB组合箱梁有限元模型见图8所示。在每个测试截面上布置应变测试元件，应变测点各个测试截面混凝土顶板布置9个混凝土应变片，钢底板布置5个钢应变片。

单位：mm

图7 CSWSB连续组合箱梁均布荷载加载图

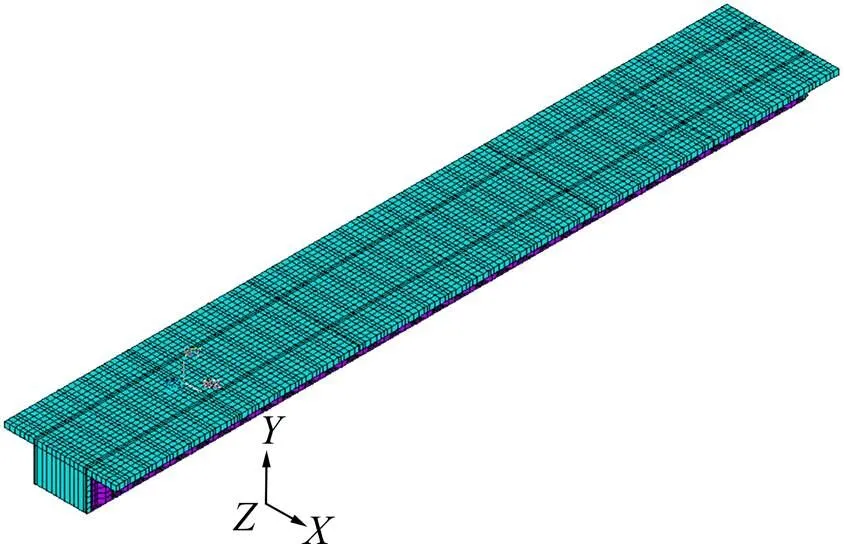
图8 单箱单室CSWSB组合箱梁的有限元模型

以制作的模型试验单箱单室CSWSB简支组合箱梁为例，分别在集中荷载和全梁纵向施加均布荷载作用时，集中荷载为71.2 kN，均布荷载为9.375 kN/m。运用推导的求解剪力滞系数表达式求得跨中截面处顶底板的理论值，并与Ansys有限元值及模型试验实测值进行对比，如图9和图10所示。

由图9和图10可知，推导的求解CSWSB 2等跨连续组合箱梁不同荷载工况下的剪力滞系数表达式，求得中间支点截面处和跨中截面处混凝土顶板和钢底板的理论值，与Ansys有限元值及模型试验实测值进行对比，3种方法计算的剪力滞系数变化规律一致，验证了简支组合箱梁在集中荷载和均布荷载作用下剪力滞系数表达式正确。集中荷载作用的剪力滞效应比均布荷载作用下的剪力滞效应明显，上翼缘板的剪力滞效应比下翼缘板的剪力滞效应明显。

图9 CSWSB简支梁集中荷载跨中剪力滞系数

图10 CSWSB简支梁均布荷载跨中剪力滞系数

3.2 CSWSB组合箱梁有效分布宽度对比分析

根据单箱单室CSWSB简支组合箱梁，在跨中截面增加一个固定支座，一侧的固定支座变换为活动支座，使该模型试验简支组合箱梁成为(4+4) m等跨连续组合箱梁。根据箱形梁设计理论提出的翼缘有效分布宽度来考虑剪力滞效应的影响，计算出CSWSB组合箱梁的翼缘有效分布宽度，并与《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG3362—2018)和《钢−混凝土组合桥梁设计规范》(GB50917—2013)中给出的箱型截面梁翼缘有效宽度公式的计算值对比，列于表1。

由表1分析可知，按《公路钢筋混凝土及预应力混凝土桥涵设计规范》规范计算的单箱单室CSWSB简支、连续组合箱梁跨中截面集中荷载作用下顶板的有效分布宽度比理论计算值大，即对剪力滞效应考虑不足，两者计算的差值达到了10%；其他工况和位置处计算的有效分布宽度均比理论计算值小。按《钢−混凝土组合桥梁设计规范》计算的有效分布宽度除了连续梁边支点截面底板上的比理论计算值小外，其余均比理论计算值大，两者计算的差值最大达到了20%；根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》计算CSWSB组合箱梁有效分布宽度时，局部差值较大，富余量较小，根据《钢−混凝土组合桥梁设计规范》计算CSWSB组合箱梁有效分布宽度时，整体差值偏大，设计中应给予重视。

表1 CSWSB组合箱梁的有效分布宽度规范值与本文理论值对比表

注：差值率=(理论值−规范值)/规范值。

4 结论

1) 采用推导的求解CSWSB简支组合箱梁不同的荷载工况下的剪力滞系数表达式，求得跨中截面处顶底板的理论最大值，与有限元值及实测值吻合较好，验证了求解剪力滞系数的表达式正确；集中荷载作用下的剪力滞效应比均布荷载作用下的剪力滞效应明显，上翼缘板的剪力滞效应比下翼缘板的剪力滞效应明显。

2) 根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》计算该组合箱梁翼板有效分布宽度时，与理论计算局部差值率达到了10%，富余量较小；根据《钢−混凝土组合桥梁设计规范》计算CSWSB组合箱梁有效分布宽度时，整体差值率偏大，设计中应给予重视。

[1] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 北京: 人民交通出版社, 2008: 1−50.GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen. Design theory of box girder[M]. Beijing: China Communications Press, 2008: 1−50.

[2] 吴文清, 叶见曙, 万水, 等. 波形钢腹板组合箱梁在对称加载作用下剪力滞效应的变分法求解[J]. 中国公路学报, 2003, 16(2): 47−51.WU Wenqing, YE Jianshu, WAN Shui, et al. Experimental study of shear-lag effect of composite box girders with corrugated steel webs[J]. China Journal of Highway and Transport, 2003, 16(2): 48−51.

[3] 李立峰, 彭鲲, 王文, 等. 波形钢腹板组合箱梁剪力滞效应的理论与试验研究[J]. 公路交通科技, 2009, 26(4): 78−83.LI Lifeng, PENG Kun, WANG Wen, et al. Theoretical and experimental study on shear lag effect of composite box girder with corrugated steel webs[J]. Journal of Highway and Transportation Research and Development, 2009, 26(4): 78−83.

[4] 冀伟, 蔺鹏臻, 刘世忠, 等. 波形钢腹板箱梁剪力滞效应的变分法求解[J]. 兰州交通大学学报, 2010, 29(6): 16−19.JI Wei, LIN Pengzhen, LIU Shizhong, et al. Variational principle of shear lag effect of composite box girders with corrugated steel webs[J]. Journal of Lanzhou Jiaotong University, 2010, 29(6): 16−19.

[5] 周茂定, 刘世忠, 杨子江. 波形钢腹板组合箱梁剪力滞效应的比拟杆法求解[J]. 兰州交通大学学报, 2012, 31(4): 41−44.ZHOU Maoding, LIU Shizhong, YANG Zijiang. Bar simulation method on shear lag effect of composite box girder with corrugated steel web[J]. Journal of Lanzhou Jiaotong University, 2012, 31(4): 41−44.

[6] 陈水生, 田正龙, 桂水荣, 等. 单箱多室波形钢腹板箱梁剪力滞研究[J]. 公路交通科技, 2015, 32(7): 69−75.CHEN Shuisheng, TIAN Zhenglong, GUI Shuirong, et al. Research on shear lag of single-box multi-cell girder with corrugated steel webs[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 69−75.

[7] 卫星, 杨世玉. 单箱双室波形钢腹板PC箱梁剪力滞效应分析[J]. 铁道工程学报, 2017, 222(3): 29−33.WEI Xing, YANG Shiyu. Research on shear lag effect in twin-cell pc box girder with corrugated steel web[J]. Journal of Railway Engineering Society, 2017, 222(3): 29−33.

[8] 石聪. 双箱单室波纹钢腹板组合箱梁剪力滞效应分析[D]. 兰州: 兰州交通大学, 2017.SHI Cong. Research on shear lag effect of single room double box girder with beam bridge with corrugated steel web[D]. Lanzhou: Lanzhou Jiaotong University, 2017.

[9] 操俊林. 新型波形钢腹板组合箱梁剪力滞效应的理论分析及试验研究[D]. 兰州: 兰州交通大学, 2018.CAO Junlin. Theoretical analysis and experimental study on shear lag effect of the new composite box-girder with corrugated steel webs[D]. Lanzhou: Lanzhou Jiaotong University, 2018.

[10] JTG D62—2018, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2018, Specifications for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].

[11] 程坤. 大跨度变截面波形钢腹板组合连续箱梁有效分布宽度研究[D]. 南昌: 华东交通大学, 2017. CHENG Kun. Research on effective distribution width of long-span box girder with corrugated steel webs and various cross-section[D]. Nanchang: East China Jiaotong University, 2017.

[12] 赵品, 荣学亮, 叶见曙. 波形钢腹板组合箱梁横向受力有效分布宽度研究[J]. 湖南大学学报(自然科学版), 2016, 43(7): 105−110.ZHAO Pin, RONG Xueliang, YE Jianshu. Research on the lateral effective width of composite box-girder with corrugated steel webs[J]. Journal of Hunan University (Natural Sciences Edition), 2016, 43(7): 105−110.

[13] Asokendu Samanta, Madhujit Mukhopadhyay. Finite element static and dynamic analyses of folded plates[J]. Engineering Structures, 1999, 21: 277−287.

Study on effective distribution width of composite box girder bridge with corrugated steel webs-flat steel floor-concrete roof

MA Chi, LIU Shizhong, CHEN Quan, WANG Junlou

(College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Considering the different modulus of concrete roof and steel floor, the governing differential equations and boundary conditions of shear lag effect of corrugated steel web-steel floor-concrete roof (CSWSB) composite box girder were derived by variational method. The shear lag coefficients of CSWSB simple supported composite box girder under concentrated load and uniform load in midspan were established. Based on the formula for calculating the effective distribution width, the shear lag effect and effective distribution width of single-box and single-compartment composite box girders under two loading conditions were analyzed by using model test beams. The results show that the expressions of shear lag coefficient of simple-supported composite box girders under concentrated and uniformly distributed loads are correct, and the shear lag effect under concentrated loads is correct. The shear lag effect of the upper flange slab is more obvious than that of the lower flange slab under uniform load. When calculating the effective distribution width of the flange slab of the CSWSB composite box girder according to the Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts, the local difference between the calculation and the theoretical calculation reaches 10%, which is surplus.Compared with the calculation of effective distribution width of CSWSB composite box girder wing slab in Code for Design of Steel-concrete Composite Bridges, the overall difference rate is too large, which should be paid attention to in design.

corrugated steel web; composite box girder; variational method; shear lag coefficient; effective distribution width

U443.35

A

1672 − 7029(2020)05 − 1178 − 08

10.19713/j.cnki.43−1423/u.T20190703

2019−08−06

国家自然科学基金资助项目(51868040，51568036)；兰州交通大学青年科学基金资助项目(2018015)

马弛(1985−)，男，甘肃文县人，副教授，博士，从事桥梁结构分析与设计理论研究；E−mail：machi0208244@163.com

(编辑 涂鹏)