考虑土体剪胀性的富水盾构隧道掌子面支护反力非线性上限解

张佳华，凌涛

考虑土体剪胀性的富水盾构隧道掌子面支护反力非线性上限解

张佳华1，凌涛2

(1. 湖南科技大学 南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室，煤矿安全开采技术湖南省重点实验室，湖南 湘潭 411201；2. 中铁五局集团 第一工程有限责任公司，湖南 长沙 410117)

考虑土体剪胀性和孔隙水效应，在非线性破坏准则下研究盾构隧道掌子面的稳定性。利用极限分析上限法构建盾构隧道掌子面的对数螺旋曲线破坏机构，根据虚功率原理推导掌子面支护反力的解析解，利用序列规划算法得到了支护反力的最优解。研究结果表明，假定土体服从相关联流动法则，会明显低估支护反力，相对误差可达到29%。不考虑孔隙水效应，会显著低估支护反力，相对误差可达到56%。此外，土体剪胀系数以及孔隙水压力系数对掌子面的破坏范围也有显著影响。建议在计算盾构掘进推力时，应该考虑土体的剪胀性、破坏准则的非线性以及孔隙水效应，否则会造成结果严重偏小而导致掌子面发生坍塌破坏。

隧道掌子面；极限分析；非关联流动法则；孔隙水；支护反力

在盾构掘进过程中，掌子面经常发生坍塌事故，造成盾构机“卡死”，这不仅严重影响施工进度，还有可能造成地面塌陷而引起重大安全事故。因此，维持隧道掌子面稳定性是盾构安全施工的关键，也是现阶段工程师们研究的重点和难点[1]。极限分析方法是研究隧道工程稳定性问题的一种有效途径[2−3]。基于线性Mohr-Coulomb破坏准则，邱业建等[4]采用上限法计算了隧道围岩的支护反力；陈峥等[5]利用上限法探究了超前支护下的隧道掌子面稳定性。事实上，土体一般服从非线性破坏准则，线性破坏准则只是非线性破坏准则的一种情况[6−8]。张佳华等[7]通过求解非线性准则下隧道支护反力及安全系数，验证了非线性系数对隧道稳定性有较大影响；张道兵等[8]基于非线性破坏准则，探究了硐室中围岩压力最优上限解，为支护设计提供有效依据。但是，上述研究均假定土体服从相关联流动法则，然而，众多学者研究发现，土体材料服从非关联流动法则[9−10]。赵炼恒等[11]研究了非关联流动法则下剪胀系数对隧道稳定性的影响。吕绍文[12]基于非关联流动法则研究双线隧道之间的影响。以上文献在研究隧道的稳定性方面取得了一系列重要的成果，但是均没有考虑孔隙水的影响。众所周知，孔隙水广泛赋存在土体中，且影响不容忽 视[13−14]。因此，本文基于非线性Mohr-Coulomb破坏准则，同时考虑土体剪胀性和孔隙水效应，研究隧道掌子面的稳定性，求解掌子面所需要的支护反力。

1 定义与定理

1.1 非线性Mohr-Coulomb破坏准则

为了准确反映土体的受力特征，工程上一般采用非线性Mohr-Coulomb破坏准则进行计算，其表达式如下[15]：

式中：为剪应力；n为正应力；0为土体初始黏聚力，为非线性系数；t为轴向抗拉强度。

1.2 非关联流动法则

研究表明，由于土体材料具有剪胀性，在发生塑性流动时，一般服从非关联流动法则[9−12]。如果假定土体服从相关联流动法则，往往会高估了剪胀角，给计算结果带来较大误差[10−11]。在考虑土体服从非线性M-C破坏准则和非关联流动法则时，一些学者提出对非线性M-C破坏准则中的初始黏聚力0进行修正，如图1所示，修正后的非线性M-C破坏准则为[16−18]：

相应的切线表达式为：

1.3 孔隙水压力效应下的上限定理

孔隙水普遍赋存在土体中，对工程的影响不容忽视[19−20]。Bishop在计算孔隙水压力时认为孔隙水压力是土重应力的一部分。由于概念清晰，计算简单，该方法得到了广泛的推广和应用，其表达式如下[20]：

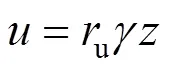
式中：u为孔隙水压力系数；为土体任意点到地表的竖直方向上的距离；为土体容重。

在采用极限分析法研究孔隙水压力影响时，通常将孔隙水压力当作内力或者外力计算，但2种方法结果一致，具体表达式为[21−22]：

然而，将孔隙水压力视为外力时，其物理意义更清晰，因此该方法得到广泛应用[21−22]。本文也将孔隙水压力作为外力进行计算。综上所述，在机动容许的速度场中，在外力做功功率与土体内部能量耗散功率相等的情况下，计算得到的荷载是大于或等于极限状态下的真实荷载，考虑孔隙水压力效应的上限定理可以表述为[23−24]：

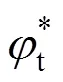
2 破坏机构

本文构建的盾构隧道掌子面双对数螺旋曲线破坏机构如图2所示，破坏机构区域由和2条对数螺旋曲线和隧道掌子面构成，且2条对数螺旋线都以角速度绕点旋转。

图2 盾构隧道掌子面双对数螺旋曲线破坏机构

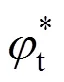
式中：1和2表示和与竖直方向的夹角；a和b表示和的长度。

通过图2中的几何关系可得：

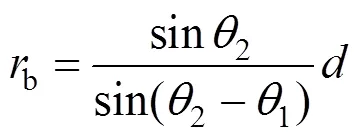
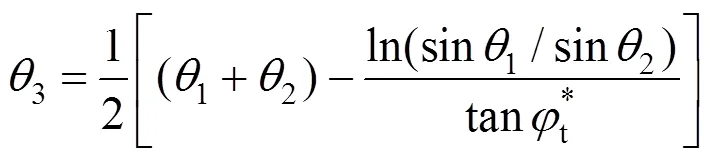
式中：为掌子面高度；3为与竖直方向的夹角。

3 计算过程

3.1 土体重力功率

若直接计算土体重力做功功率较为复杂，本文采用叠加法将土体区域拆分为′，，′，4个区域，分别计算各区域土体重力 功率。

区域′重力做功功率，记为1：

其中

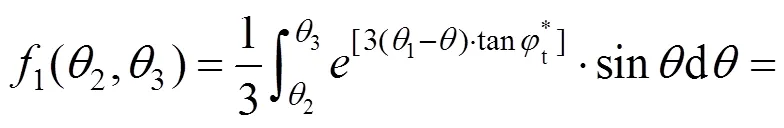
同理，区域内土体重力做功功率记为2：

其中

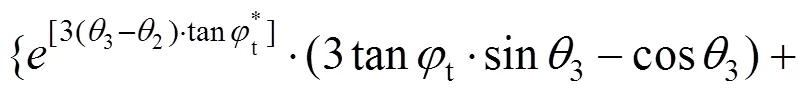
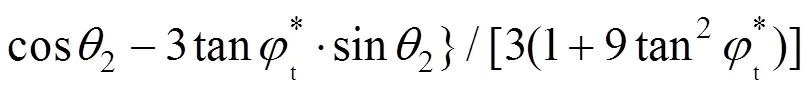
′区域内土体重力做功功率记为3：

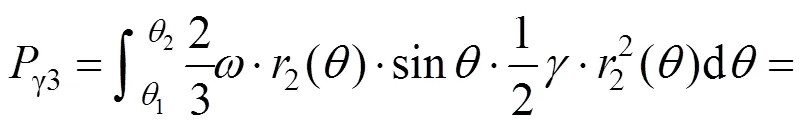
其中

区域内土体重力做功功率记为4：

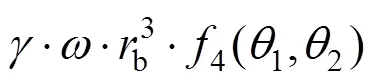
其中

综上所述，土体重力做功功率为：

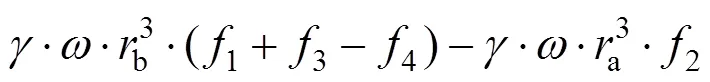
3.2 孔隙水压力功率

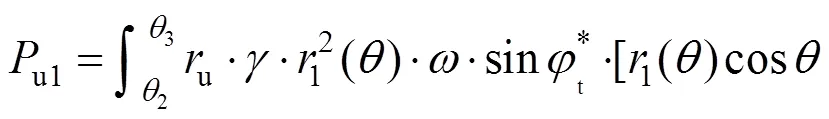
其中

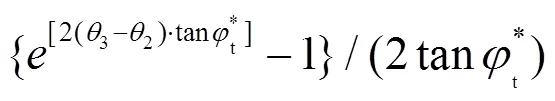
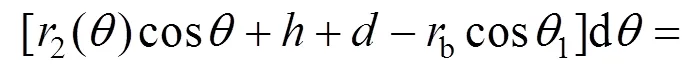
其中

综上所述，孔隙水压力所做的总功率为：

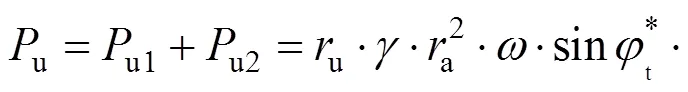
3.3 支护反力功率

如图2中的破坏模式，均布荷载T为所求支护反力，且只在掌子面上做功，其功率为：

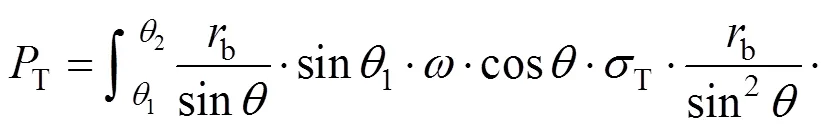
3.4 内能耗散率

由于内部能量损耗只发生在速度间断线和上，内能耗散率为：

式中：V1为速度间断线上的能量耗散率；V2为速度间断线上的能量耗散率。

3.5 支护反力上限解

由上述公式可得支护反力解析解，具体为：

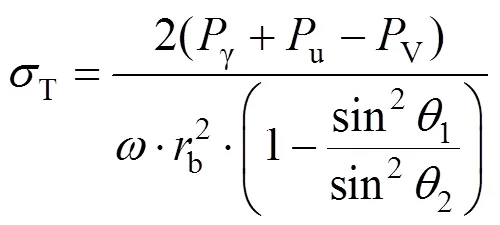
4 结果分析

4.1 对比

姚聪等[16]求解了盾构隧道掌子面维持稳定所需的支护反力，为了与其进行对比，本文令孔隙压力水系数u=0，即不考虑孔隙水作用，将结果与文献[16]对比。参数取值如下：=8 m，=18 kN/m3，t=30 kPa，=30 m，0=10 kPa，=1.2，=0.8，u=0.1~0.5。

如表1所示，当孔隙水压力系数u=0时，本文和文献[16]结果一致，求解的盾构掌子面支护反力T都为85.6 kPa，验证了本文计算方法的正确性。本文考虑孔隙水效应，令u=0.1~0.5时，随着孔隙水压力系数u增大，掌子面支护反力T也增大。与不考虑孔隙水压力(u=0)时求解的掌子面支护反力T相比，相对误差最小为56%，最大为282%，表明孔隙水对隧道掌子面支护反力有显著影响，因此孔隙水效应不容忽视。建议在富水区段施工时，应加强掌子面支护反力，以防止发生坍塌事故。此外，文献[16]没有考虑孔隙水效应，只是本文研究成果中的一个特例。

表1 不同孔隙水压力系数下的支护反力

4.2 支护反力

(a) m-c0-σT; (b) c0-m-σT; (c) η-c0-σT; (d) η-m-σT; (e) ru-h-σT; (f) h-ru-σT

4.3 破坏面

为研究各参数对隧道掌子面破坏面影响，各参数取值如下：=10 m，=18 kN/m3，t=30 kPa，=30 m，0=10 kPa，=1.3，=0.8，u=0.3。当非线性系数增大或初始黏聚力0减小时，掌子面的破坏面向外延伸，破坏高度增加，破坏范围增大。当孔隙水压力系数u增大时，破坏面向洞内靠近，破坏高度减小，破坏范围减小。随着地下水位线高度增加，破坏面逐渐向外发展。随着剪胀系数减小，隧道破坏面向外延伸，破坏高度增加，破坏范围增大。由此可见，非线性系数，初始黏聚力0，剪胀系数，孔隙水压力系数u以及水位线高度对隧道掌子面潜在破坏面均有较大影响。

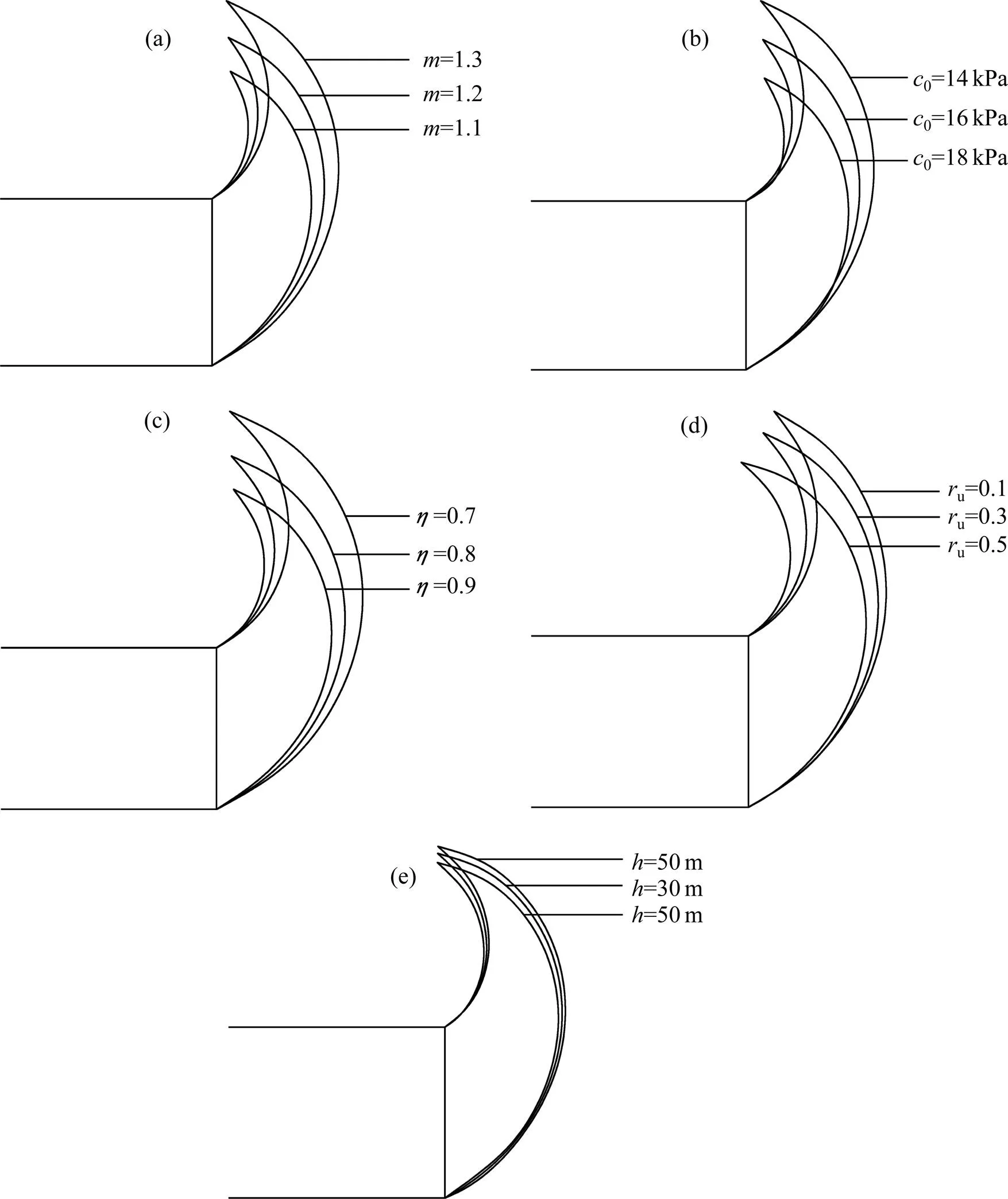
(a) 非线性系数；(b) 初始黏聚力；(c) 剪胀系数；(d) 孔隙水压力系数；(e) 水位线高度

5 结论

1) 基于非线性Mohr-Coulomb破坏准则及非关联流动法则，推导了孔隙水作用下隧道掌子面支护反力的解析解，采用序列二次规划算法得到了掌子面支护反力的最优上限解。

2) 不考虑孔隙水时，令u=0，本文求解的支护反力与文献[16]结果一致，验证了本文计算方法的正确性，同时也表明文献[16]只是本文研究的一种情况。

3) 当非线性系数增大、初始黏聚力0减小、剪胀系数减小、孔隙水压力系数u增大或地下水位线高度增大时，掌子面支护反力T增大。对比=1.1与=1.5，支护反力相对误差为13%。对比=1.0(土体服从相关联流动法则)和=0.6(土体服从非关联流动法则)，支护反力相对误差为29%。对比u=0(不考虑孔隙水)与u=0.5(考虑孔隙水)，支护反力相对误差为282%。如果假定土体服从线性破坏准则、相关联流动法则或不考虑孔隙水效应，会严重低估盾构隧道掌子面的支护反力。

4) 当非线性系数或地下水位线高度增大时，掌子面破坏面向外延伸，破坏高度增加，破坏范围增大。当初始黏聚力0,剪胀系数或孔隙水压力系数u增大时，破坏面向洞内靠近，破坏高度减小，破坏范围减小。

[1] 吴梦军, 陈彰贵, 许锡宾, 等. 公路隧道围岩稳定性研究现状与展望[J]. 重庆交通学院学报, 2003, 22(2): 24−28.WU Mengjun, CHEN Zhanggui, XU Xibin, et al. The present and prospect of highway tunnel surrounding rock stability[J]. Journal of Chongqing Jiaotong University, 2003, 22(2): 24−28.

[2] 黄茂松, 宋春霞, 吕玺琳. 非均质黏土地基隧道环向开挖面稳定上限分析[J]. 岩土工程学报, 2013, 35(8): 1504−1512. HUANG Maosong, SONG Chunxia, LÜ Xilin. Upper bound analysis for stability of a circular tunnel in heterogeneous clay[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1504−1512.

[3] Subrin D, Wong H. Tunnel face stability in frictional material: A new 3D failure mechanism[J]. Comptes Rendus Mecanique, 2002, 330(7): 513−519.

[4] 邱业建, 彭立敏, 雷明锋. 浅埋偏压隧道围岩压力上限法解析解[J]. 土木工程学报, 2015, 48(6): 106−113. QIU Yejian, PENG Limin, LEI Mingfeng. Upper bound solutions for surrounding rock pressure of shallow bias tunnel[J]. China Civil Engineering Journal, 2015, 48(6): 106−113.

[5] 陈峥, 何平, 颜杜民, 等. 超前支护下隧道掌子面稳定性极限上限分析[J]. 岩土力学, 2019, 40(6): 2154−2162. CHEN Zheng, HE Ping, YAN Dumin, et al. Upper-bound limit analysis of tunnel face stability under advanced support[J]. Rock and Soil Mechanics, 2019, 40(6): 2154−2162.

[6] 张佳华, 杨小礼, 张标, 等. 基于非线性破坏准则的浅埋偏压隧道稳定性分析[J]. 华南理工大学学报(自然科学版), 2014, 42(8): 97−103, 121. ZHANG Jiahua, YANG Xiaoli, ZHANG Biao, et al. Stability analysis of shallow bias tunnels based on nonlinear failure criterion[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(8): 97−103, 121.

[7] 张佳华, 张标. 非线性破坏准则下浅埋隧道支护参数上限解[J]. 铁道科学与工程学报, 2018, 15(8): 2062− 2071. ZHANG Jiahua, ZHANG Biao. Upper bound solutions of support parameter for shallow tunnels in nonlinear soil masses[J]. Journal of Railway Science and Engineering, 2018, 15(8): 2062−2071.

[8] 张道兵, 王卫军. 用非线性M-C破坏准则计算深埋硐室围岩压力上限解[J]. 矿业工程研究, 2017, 32(4): 1−8. ZHANG Daobing, WANG Weijun. Upper bound solution to surrounding rock pressure for deep cavity by using nonlinear M-C failure criterion[J]. Mineral Engineering Research, 2017, 32(4): 1−8.

[9] 孔位学, 芮勇勤, 董宝弟. 岩土材料在非关联流动法则下剪胀角选取探讨[J]. 岩土力学, 2009, 30(11): 3278− 3282. KONG Weixue, RUI Yongqin, DONG Baodi. Determination of dilatancy angle for geomaterials under non-associated flow rule[J]. Rock and Soil Mechanics, 2009, 30(11): 3278−3282.

[10] 王凤云, 钱德玲. 基于统一强度理论深埋圆形隧道围岩的剪胀分析[J]. 岩土力学, 2019, 40(5): 1966−1976. WANG Fengyun, QIAN Deling. Dilatancy analysis for a circular tunnel excavated in rock mass based on unified strength theory[J]. Rock and Soil Mechanics, 2019, 40(5): 1966−1976.

[11] 赵炼恒, 孙秋红, 黄阜, 等. 非关联流动准则对浅埋隧道稳定性影响的上限分析[J]. 公路交通科技, 2012, 29(12): 101−106. ZHAO Lianheng, SUN Qiuhong, HUANG Fu, et al. Influences of non-associated flow rule on shallow tunnel stability based on upper bound limit analysis[J]. Journal of Highway and Transportation Research and Development, 2012, 29(12): 101−106.

[12] 吕绍文. 非关联流动法则对双线平行隧道上限解的影响分析[J]. 公路工程, 2014, 39(3): 260−263, 303.LÜ Shaowen. The influence analysis of non-associate flow rule on the upper limit solution of two parallel tunnels[J]. Highway Engineering, 2014, 39(3): 260−263, 303.

[13] 宋子亨, 杨强, 刘耀儒. 考虑孔隙水压力作用的岩土体弹塑性模型及其有限元实现[J]. 岩土力学, 2016, 37(增1): 500−508. SONG Ziheng, YANG Qiang, LIU Yaoru. Elastoplastic model for geomaterial considering effect of pore water pressure and its finite elements implementation[J]. Rock and Soil Mechanics, 2016, 37(Suppl 1): 500−508.

[14] 黄阜, 杨小礼, 黄戡, 等. 考虑孔隙水压力效应和非线性破坏准则的浅埋地下洞室支护力上限分析[J]. 岩土工程学报, 2011, 33(12): 1903−1909. HUANG Fu, YANG Xiaoli, HUANG Kan, et al. Upper bound solutions of supporting pressure of shallow cavities subjected to ore water pressure based on nonlinear failure criterion[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1903−1909.

[15] ZHANG Jiahua, WANG Chengyang. Energy analysis of stability onshallow tunnels based on non-associated flow rule and non-linearfailure criterion[J]. Journal of Central South University, 2015, 22(3): 1070−1078.

[16] 姚聪, 杨小礼. 基于非关联流动法则的盾构隧道掌子面稳定性上限分析[J]. 矿冶工程, 2016, 36(4): 26−29. YAO Cong, YANG Xiaoli. Upper bound limit analysis for the stability of shield tunnel working face subjected to non-associated flow rule[J]. Mining and Metallurgical Engineering, 2016, 36(4): 26−29.

[17] YANG X L, HUANG F. Three-dimensional failure mechanism of a rectangular cavity in a Hoek-Brown rock medium[J]. International Journal of Rock Mechanics and Mining Sciences, 2013(61): 189−195.

[18] 刘世伟, 盛谦, 朱泽奇, 等. 隧道围岩内地下水渗流边界效应影响研究[J]. 岩土力学, 2018, 39(11): 4001− 4009. LIU Shiwei, SHENG Qian, ZHU Zeqi, et al. Research on boundary effect of groundwater seepage in tunnel surrounding rock[J]. Rock and Soil Mechanics, 2018, 39(11): 4001−4009.

[19] 魏新江, 陈伟军, 魏纲, 等. 盾构隧道施工引起的土体初始超孔隙水压力分布研究[J]. 岩土力学, 2012, 33(7): 2103−2109. WEI Xinjiang, CHEN Weijun, WEI Gang, et al. Research on distribution of initial excess pore water pressure due to shield tunnelling[J]. Rock and Soil Mechanics, 2012, 33(7): 2103−2109.

[20] Bishop A W. The use of the slip circle in the stability analysis of slopes[J]. Geotechique, 1955, 5(1): 7−17.

[21] CHEN W F, LIU X L. Limit analysis in soil mechanics[M]. Amsterdam: Elsevier, 1990.

[22] CHEN W F. Limit analysis and soil plasticity[M]. Florida: J Ross Publishing, Inc, 2007.

[23] HUANG Fu, ZHANG Daobing, SUN Zhibin, et al. Influence of pore water pressure on upper bound analysis of collapse shape for square tunnel in Hoek-Brown media[J]. Journal of Central South University of Technology, 2011, 18(2): 530−535.

[24] Michalowski R L, Nadukuru S S. Three-dimensional limit analysis of slopes with pore pressure[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 139(9): 1604−1610.

[25] 张佳华, 王卫军, 张道兵, 等. 考虑Hoek-Brown准则和孔压效应隧道掌子面可靠度分析[J]. 铁道科学与工程学报, 2018, 15(12): 3173−3180. ZHANG Jiahua, WANG Weijun, ZHANG Daobing, et al. Reliability analysis of tunnel face considering the effect of pore water pressure and Hoek-Brown failure criterion[J]. Journal of Railway Science and Engineering, 2018, 15(12): 3173−3180.

Upper bound solution of supporting pressure of shield tunnel faces considering soils dilatancy and the pore water under the nonlinear failure criterion

ZHANG Jiahua1, LING Tao2

(1. Work Safety Key Lab on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines, Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China; 2. The First Engineering Co. Ltd. of China Railway Wuju Group, Changsha 410117, China)

The stability of shield tunnel faces was investigated with the nonlinear failure criteria considering the pore water effect and dilatancy of soils. A logarithmic spiral curve failure mechanism of shield tunnel faces was constructed by using the limit analysis method. The analytical solution of support pressure was derived according to the virtual power principle. The optimal solution of support pressure was obtained by the sequence programming algorithm. The results show that if soils are assumed to obey the associated flow rule, the support pressure will be underestimated obviously, whose relative error can reach 29%. Similarly, if the pore water is not considered, the relative error of support pressure will be to reach 56%. In addition, the dilatancy coefficient of soils and the pore water pressure coefficient also have a significant impact on the failure scope of tunnel faces. It is suggested that soil dilatancy, nonlinearity of failure criterion and pore water effect should be taken into account to solve the driving force of shield, otherwise the results would be too small to cause collapse of tunnel faces.

tunnel face; limit analysis; non-associated flow rule; pore water; support pressure

TD315

A

1672 − 7029(2020)05 − 1219 − 09

10.19713/j.cnki.43−1423/u.T20190698

2019−08−04

国家自然科学基金资助项目(51804113)；湖南科技大学博士启动基金资助项目(E51768)；湖南科技大学博士后科研基金资助项目(E61610)；南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室开放基金资助项目(E21734)

张佳华(1983−)，男，湖北天门人，讲师，博士，从事隧道与地下工程方面研究；E−mail：1010090@hnust.edu.cn

(编辑 蒋学东)