单层土压密注浆压力及上抬力确定方法研究

程雪松，范洪浩，郑星伟，刘露

单层土压密注浆压力及上抬力确定方法研究

程雪松1，范洪浩1，郑星伟1，刘露2

(1.衢州市交通投资集团有限公司，浙江 衢州 324100；2. 中南大学 土木工程学院，湖南 长沙 410075)

考虑注浆过程中土体发生三维锥形剪切破坏，对单层土压密注浆压力及上抬力确定方法的进一步研究对工程实践具有特别明显的指导作用。采用球孔扩张模型和三维锥形剪切破坏模型来研究土体压密注浆加固的力学机理。将压密注浆过程视为理想土体中的球孔扩张问题，基于Mohr-Coulomb破坏准则，通过绕轴旋转将其破坏曲线改进为三维破坏模型，提出单层土压密注浆压力及上抬力的计算模型。并与其他计算结果进行对比，验证了本文方法的有效性。

单层土；压密注浆；上抬力；球孔扩张；三维破坏

注浆抬升技术的原理就是利用注浆过程中浆液产生的上抬力使建筑物发生上抬位移。建筑物注浆的关键就是经过注浆后对既有建筑物的抬升效果进行动态控制和工后恢复，以此减小建筑物的不均匀沉降。1969年，Graf[1]首先提出了可以利用压密注浆的抬升效应来纠正建筑物的偏差。Burland等[2]基于对伦敦地铁Jubilee延长线工程邻近建筑物响应的研究，对各个工段的补偿注浆过程和建筑物注浆补偿效果进行详细分析。Bolton等[3]对软黏土地层中进行隧道掘进时压密注浆的抬升效应进行研究，分析了其对地层变形的影响规律。冯旭海[4]阐述了注浆各个阶段的力学机理，并对力学机理和注浆抬升效应间的关系、注浆过程中的土体应力分布规律进行讨论。Nicholson等[5−6]建立有限元计算模型，通过对注浆单元直接施加体积应变来研究压密注浆抬升过程。易小明等[7]通过相关分析和数值模拟，对注浆抬升参数选取进行了初步优化，以及对房屋的抬升量进行了预测。但是，目前的研究中注浆过程中土层真实的破坏情况和土体层数往往没有考虑，压密注浆压力及注浆引起地表隆起时上抬力的计算也很少涉及。因此，本文采用球孔扩张模型和三维锥形剪切破坏模型来研究土体压密注浆加固的力学机理，提出单层土压密注浆压力及上抬力的计算模型，最后通过对比研究论证研究的有效性。

1 理论和模型

基于注浆加固机理的分析，可以假设注浆过程中包括以下2种机制：1) 浆泡的增大类似于土体中的球形孔扩张；2) 地面发生抬升与浆泡上方土体发生锥形剪切破坏有关。

1.1 球孔扩张模型

在大多数情况下，理想土体中的扩孔问题已被简化为在无限大均匀各向同性土体中的球形或圆柱形孔的扩张问题。压密注浆中形成的浆泡被假定为在各向同性的理想弹塑性体中的球形孔扩张，如图1所示。

开始注浆时，浆泡具有初始微小半径R；当均匀分布的内部压力逐渐增加至时，浆泡半径扩大到，围绕着浆泡的球形区域将成为塑性平衡状态。当塑性区域的半径扩大到R，R外部区域维持着弹性平衡状态。假设在施加注浆压力之前，土体内部存在着各向同性的有效应力，对比现有的和新施加的应力，将不考虑塑性区域内的体力。由于球对称条件，应力均用球坐标()表示，其剪切分量相互抵消()，所以可以得到浆泡扩张时塑性区的应力平衡方程式为：

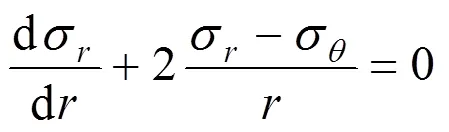
式中：r是浆泡中心到任意一点的距离；σr和σθ分别是径向和切向应力。

1.1.1 Mohr-Coulomb破坏条件

将岩土材料视为理想弹塑性体时，在弹塑性边界上必须满足Mohr-Coulomb破坏准则，其极限平衡条件表示为：

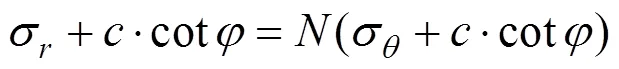
解出，有：

1.1.2 塑性区径向应力求解

将式(3)代入塑性区应力平衡方程式(1)中，可以得到微分方程：

边界条件为：当时，=。解上式的微分方程，可以得到塑性区的径向应力：

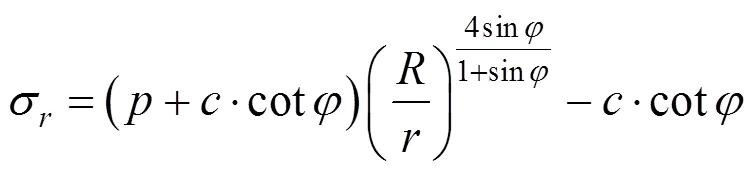
1.1.3 体积守恒定律

球孔扩张的过程遵循体积守恒定律，即孔的体积变化等于塑性区和弹性区的体积变化之和。设R是浆泡扩张之前的初始半径，是对应极限注浆压力的浆泡最终半径，因此：

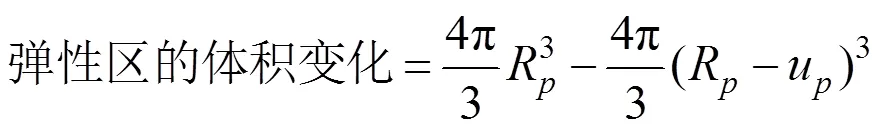
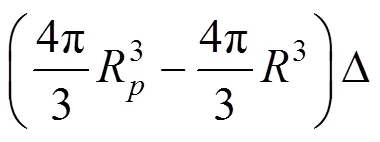
式中：u是塑性区边界的径向位移，可从著名的拉梅解中解得。

1.1.4 径向位移的求解

根据经典的弹性理论，可以用应变势分别表示应力和位移：

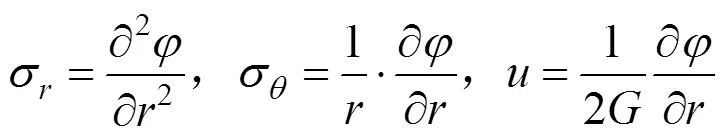
定义应变势为：

式中：为常数；为坐标原点到所考虑点的距离；

可以得到：

于是有：

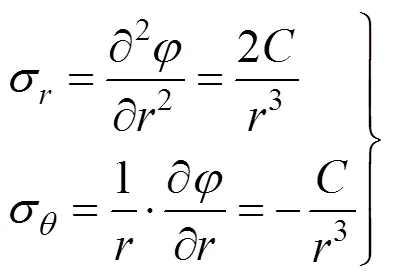
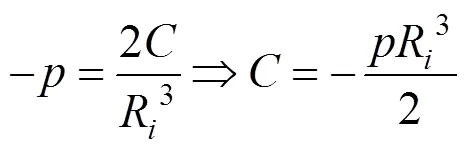
将常数代入式(10)和(12)，可以得到应力函数为：

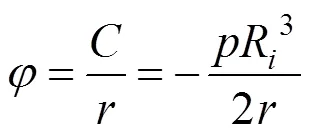
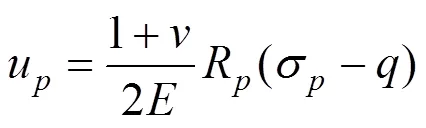
由式(5)，径向应力可以表示为：

联立式(16)和式(17)可以求得径向位移u：

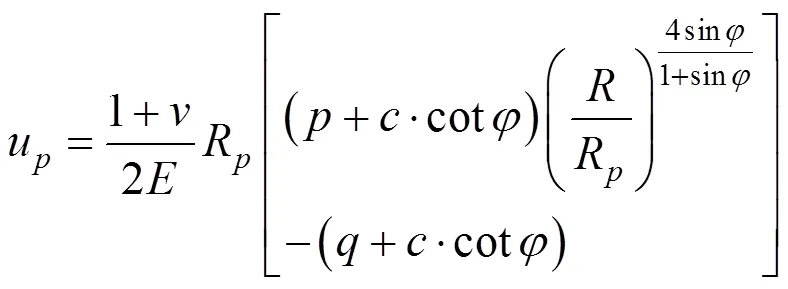
1.1.5 弹塑性交界面处应力分量的平衡条件

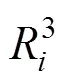
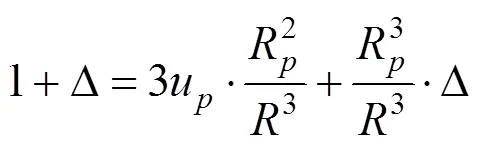
将式(18)代入式(19)，得：

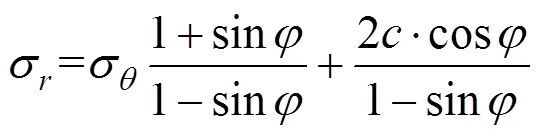
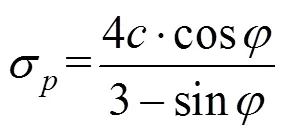
将式(23)代入式(17)中，可以得到：

假设在施加注浆压力之前，土体内部存在着各向同性的有效应力，因此可以求得弹塑性交界面处应力分量的平衡条件为：

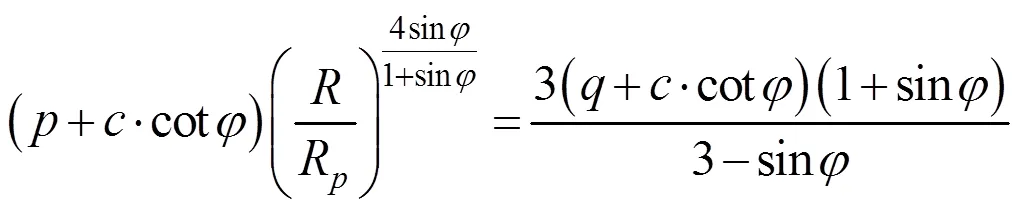
1.1.6 刚度指标及R/的比值

把式(25)代入式(20)，并化简可以得：

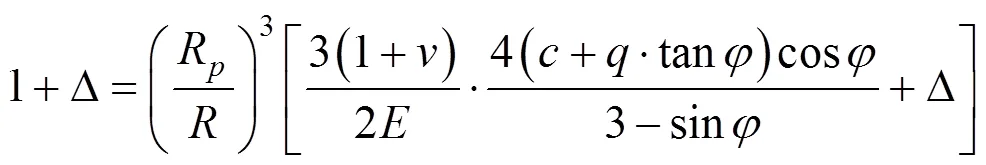
引入刚度指标I：

所以式(2)~(27)可以化简成：

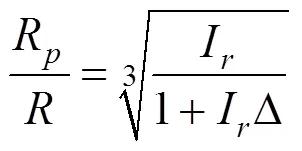
若引入修正刚度指标I：

将式(31)代入式(30)，R/比值的表达式可化简为：

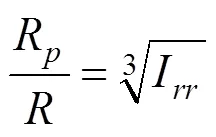
表1给出了根据不同介质计算出来的刚度指标I和相应R/比值。

表1 刚度指标Ir的参考值

1.2 三维锥形剪切破坏模型

压密注浆过程中，若注浆压力或注浆时间达到或超过某一确定值，浆泡上方土体发生了剪坏破坏产生隆起现象。根据Graf[1,8]的观察结果，可以合理地假设，当地面开始被抬升时，浆泡所施加的向上的力等于浆泡上方锥形土体的自重加上锥形面上的抗剪力。如图2所示。

基于ZOU等[9]的分析，注浆时土体破坏面的曲线方程可以表示为：

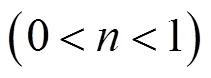
其中，和表示为：

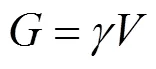
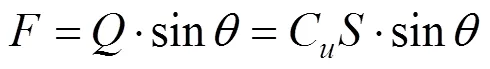
式中：为浆泡半径；为破坏面与水平方向的夹角；p为注浆压力，这里指注浆过程中发生上抬现象时所需的压力；为注浆体上方类似倒圆台的体积；为土体重度；C为土体的不排水抗剪强度；为注浆体上方类似倒圆台的侧面积。

图2 浆泡的锥形剪切破坏模型

根据旋转体体积的平衡条件可知：

注浆体上方类似倒圆台的体积的表达式为：

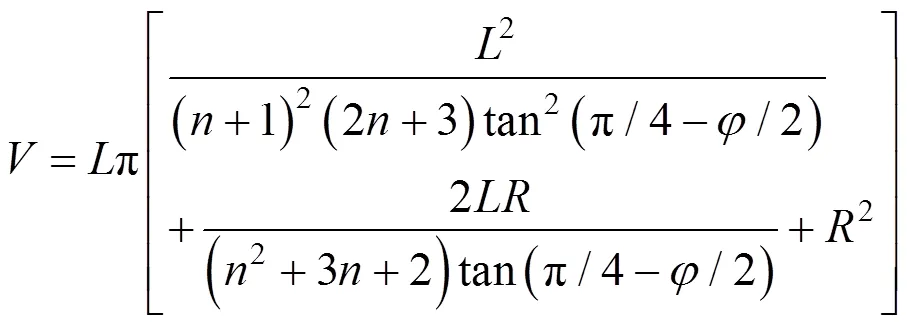
根据无穷小单元抗剪力的平衡条件，可以得到d的表达式为：

式(40)可以通过类似的方法求解，锥形面上抗剪力的表达式为：

结合式(34)，(39)和式(41)，发生抬升作用时注浆压力p和浆泡半径之间的关系表达式如下：

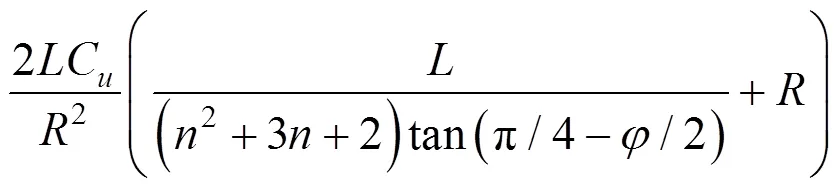
式中：是土体重度；是浆泡半径；是注浆深度；是内摩擦角；是破坏面的形状参数(0＜＜1)；C是土体的不排水抗剪强度。

从式(42)可以看出，压密注浆过程中发生上抬现象时所需的注浆压力只与注浆深度、土体重度、浆泡半径和土体的不排水抗剪强度C相关，注浆深度是影响注浆压力的最重要因素。

2 注浆压力求解

在压密注浆过程中，假设注浆一直持续到极限状态。在地表隆起处，浆泡所施加的上抬力不仅会导致上方土体发生锥形剪切破坏而且会产生向上的位移，此时所需要的注浆压力由式(42)求得。在给定深度处注浆时，只有合适的注浆压力才能使浆泡半径随之增大，从而提供地表隆起时需要的注浆压力和浆泡半径。地表隆起时压力值和浆泡半径值的确定取决于注浆过程中浆泡半径随施加压力的增加速率。基于这一点，可以求解压密注浆过程中施加的注浆压力和相应的浆泡半径之间的关系，如下所示。

将式(32)给出的R/比值代入式(25)，注浆压力的计算公式如下：

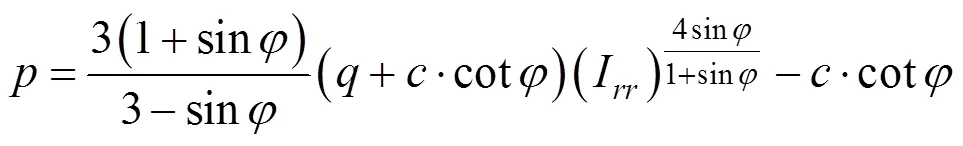
将式(43)给出的注浆压力的表达式和式(32)给出的R/比值代入式(17)中，并化简可得σ的表达式为：

将式(44)给出的σ的表达式代入式(16)中，并化简可得u/R比值的表达式为：

从式(31)中可得平均体积应变Δ的表达式 如下：

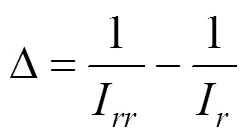
根据现场试验，当塑性区的平均体积应变Δ＞10−2时，土体会发生结构破坏，因此本文中取平均体积应变Δ=0.01。

将式(8)的等式两边同时除以3可以得到如下表达式：

然后将式(32)，(45)和式(46)代入式(47)中，可得R/的表达式为：

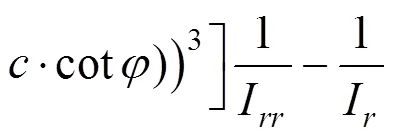
在这里，可令：

则，式(48)可以写成：

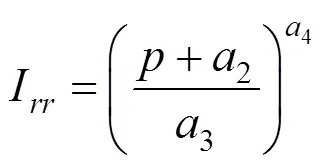
其中，2，3和4分别表示为：

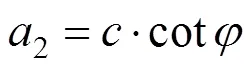
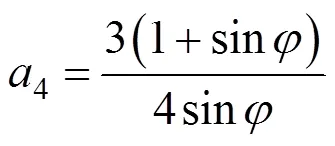
结合式(50)和(51)，R/的比值也可以表示为关于注浆压力的函数，其表达式如下：

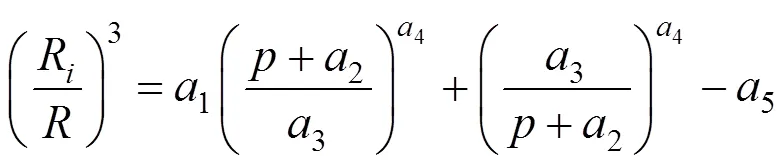
其中，5可以表示为：

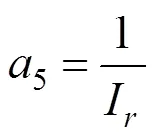
因此，式(55)也可写成如下形式，即压密注浆过程中施加的注浆压力和相应的浆泡半径之间的关系：

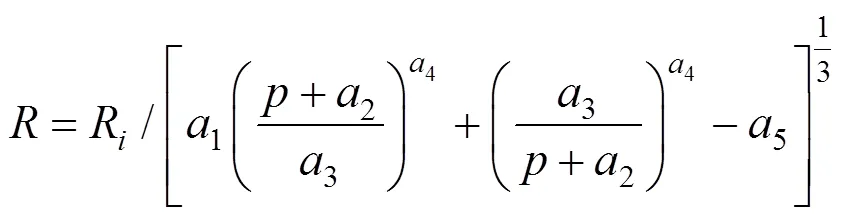
式中：是浆液−土体分界面处施加的注浆压力；是与施加的注浆压力对应的浆泡半径；R是浆泡的初始微小半径注浆；1，2，3，4和5是常数，取决于土体类型和注浆深度，分别由式(49)，(52)，(53)，(54)和(56)给出。

式(57)给出的球孔扩张模型代表注浆过程中土体的力学特性，而式(42)给出的三维锥形剪切破坏模型代表其失效状态，均可用于压密注浆压力的求解。明显可以发现，由式(57)和式(42)确定的压密注浆压力在同样的土体中并不相等。假设地层特性和上述模型中的土层特性相同，在压密注浆过程中，注浆压力将随着注浆速率和注浆时间而不断增大，当增大到确定值时(即发生抬升作用时的注浆压力uph)土体将发生锥形剪切破坏作用，再继续增大到极限值时(即极限注浆压力ult)周围土体将发生过度塑性变形，并接近破坏。虽然由式(57)可知极限注浆压力有一个确定值，但由于它要求水泥浆泡无限增长，因此无法从物理上求得。假定直到发生塑性破坏之前，周围土体都处于塑性平衡状态，发生塑性破坏时的注浆压力ex−df由极限注浆压力ult决定。

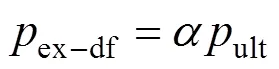
式中：是无量纲失效因数(<1.0)。

由此看得，当选取的压密注浆压力太小时，土体不能被挤密加固，而且也不能发生抬升作用；注浆压力太大时，土体会发生明显的水力劈裂现象，浆液容易沿裂缝窜到地面上。所以如何确定合适的注浆压力就显得尤为重要，本文将确定压密注浆的压力值lim为发生抬升作用时的注浆压力uph和发生塑性破坏时的注浆压力ex−df中的较小值。

根据本文提出的方法，通过MATLAB编程计算，求解压密注浆压力和上抬力；同时，也可绘制浆泡半径随注浆压力变化的曲线图。具体的计算流程如图3所示。

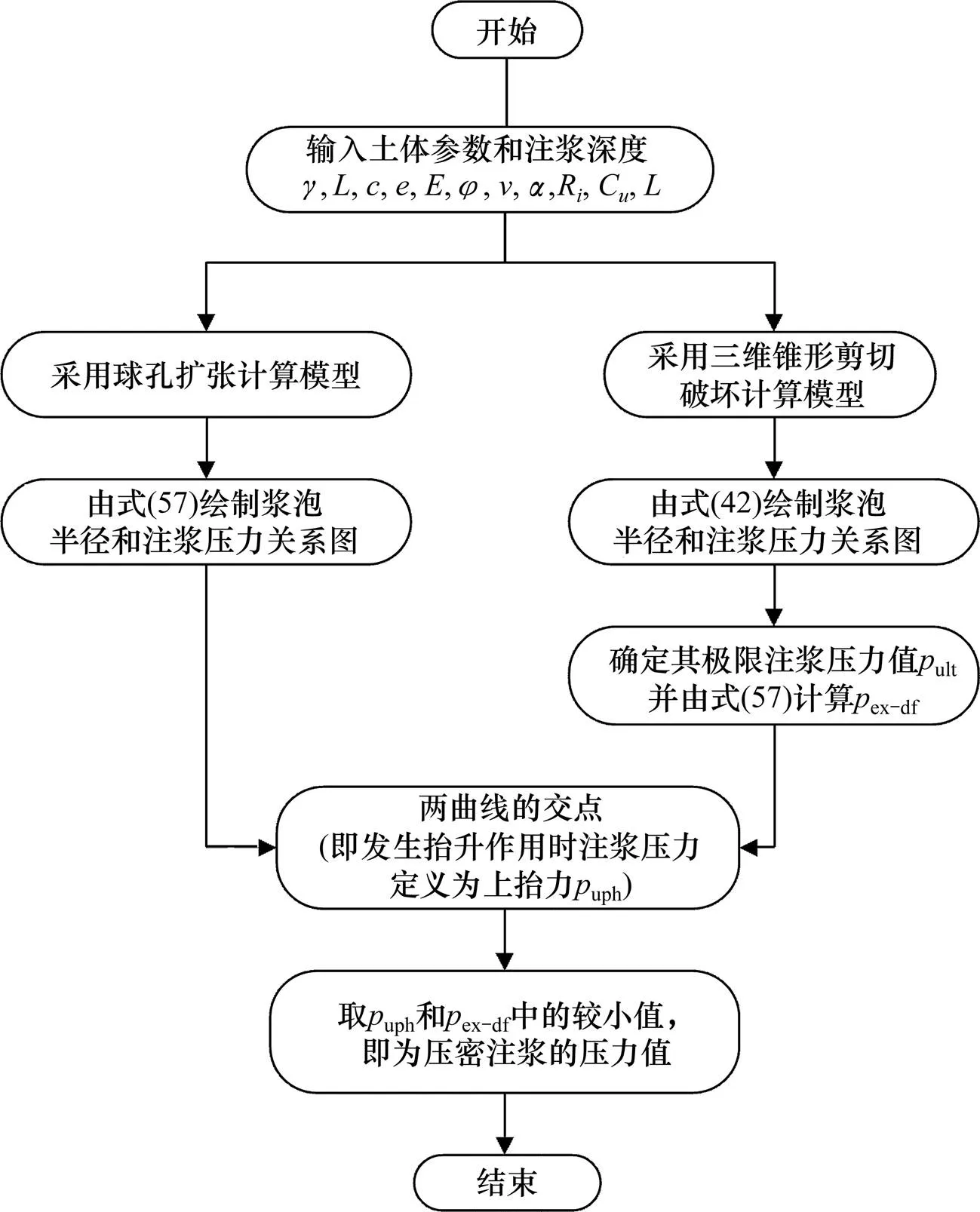
图3 计算流程图

3 验证与分析

为了验证本文计算方法的正确性，将本文方法的计算结果和EI-Kelesh等[10]的结果进行了对比分析。采用Vesic和Clough[11]理论分析时采用的参数，如表2所示，取无量纲失效因数=0.9，破坏面的形状参数=0.5。通过计算，分别得到了由El-Kelesh等[10]提出的模型、本文提出的球孔扩张模型和三维锥形剪切破坏模型计算的浆泡半径随注浆压力的变化曲线图，如图2~4所示。得到了不同土体B-4，B-5和B-6在不同注浆深度(分别为2.0，4.0和6.0 m)下的压密注浆压力预测值，如图5所示。同时还得到了土体B-5压密注浆压力在临界深度前后的变化，如图6所示。

表2 作为模型验证的土体参数(Vesic和Clough)

注：平均粒径=0.37 mm；均匀系数=2.5；比重=2.66；max=1.10；min=0.61。

如图4可知，注浆过程中球孔扩张模型表明，浆泡半径随着注浆压力的增加而增加到达到一个压力值同时也满足锥形剪切破坏模型(即2个曲线的交点)，此时的压力值被定义为土体发生抬升作用时的上抬力uph。在此模型曲线的后半段，浆泡半径急剧增加，注浆压力接近极限注浆压力ult并趋于无穷大。同时将由EI-Kelesh等[10]提出的模型和本文计算的浆泡半径与注浆压力的变化曲线进行对比，可以看出2条曲线基本重合，本文计算出的上抬力相对更大一些，但是两者之差不超过5%。

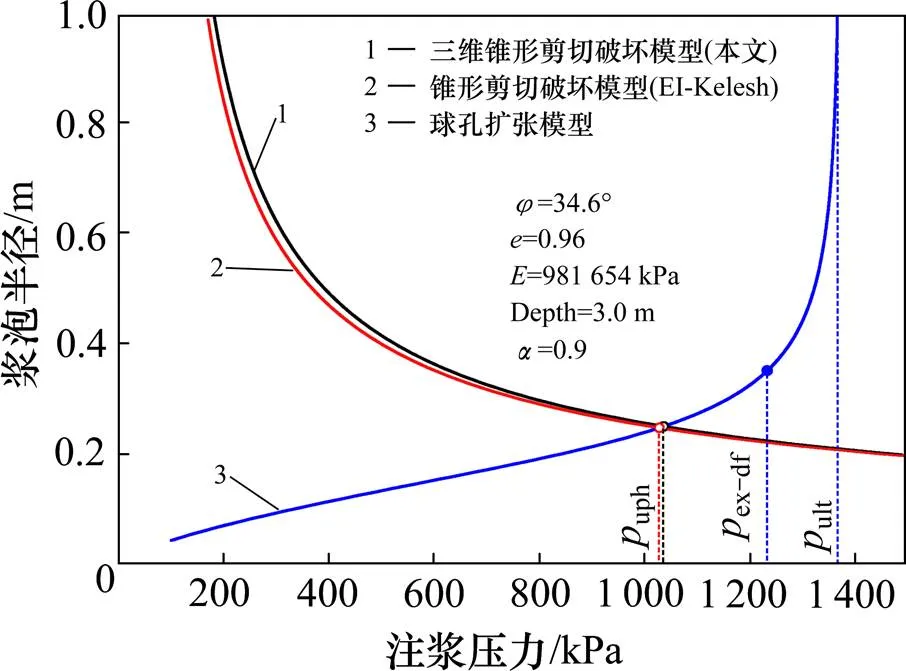
图4 浆泡半径随注浆压力的变化曲线图

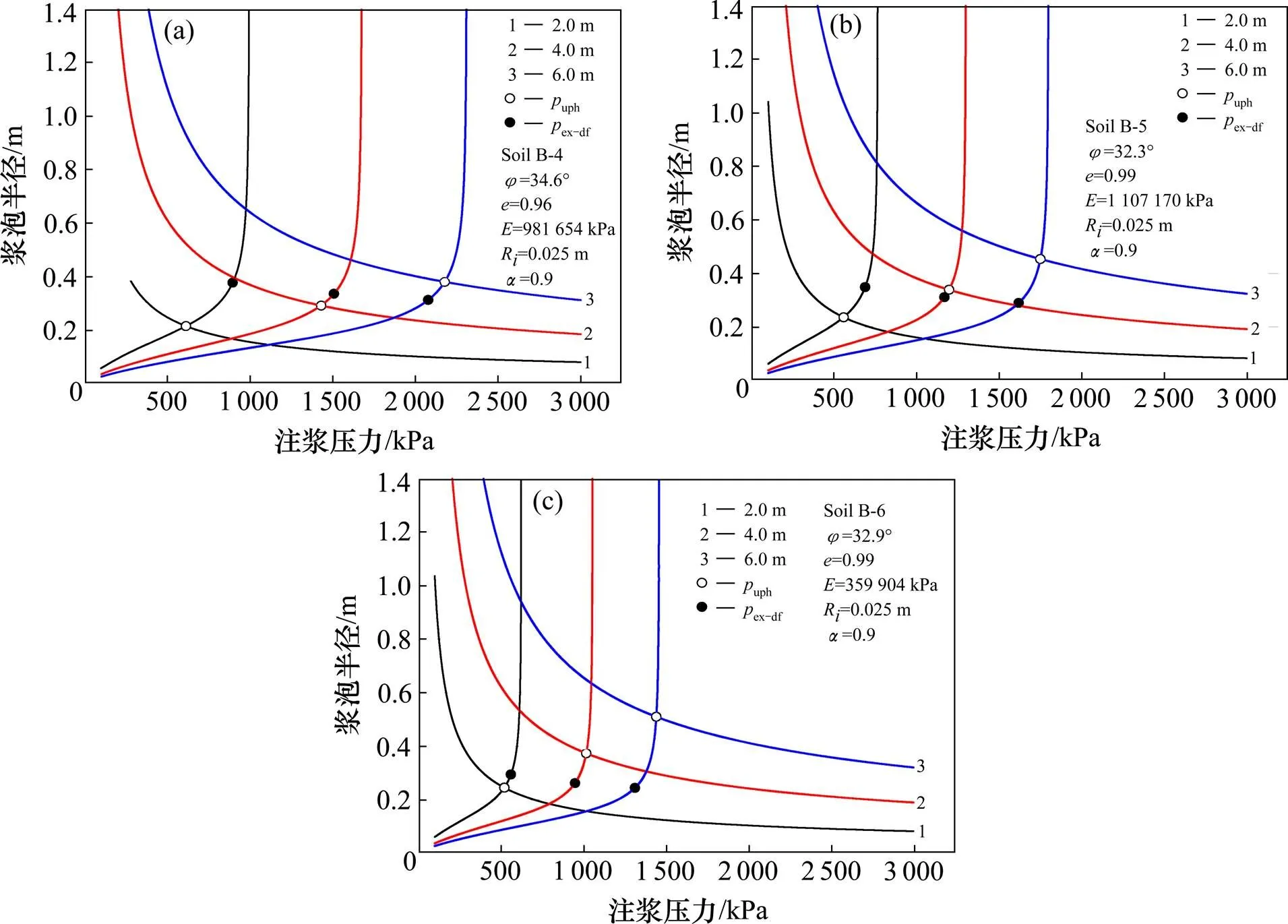
(a) 土体B-4；(b) 土体B-5；(c) 土体B-6

对压密注浆压力的研究中都没有资料给出给定注入深度时压力的特定值，所以选取压密注浆压力的下限和上限分别为350和3 500 kPa，由图5可知，不同土体B-4，B-5和B-6在不同注浆深度2.0，4.0和6.0 m的压密注浆压力预测值均在给出的实际注浆压力范围内。虽然预测的注浆压力均在给出的实际范围内，但值得注意的是，注浆深度为6.0 m时不同土体的预测注浆压力范围为1 400~2 200 kPa，远小于其上限3 500 kPa。由图6也可以看出，注浆压力随注浆深度的增加而增大；此外，注浆深度决定了注浆压力是由上抬力uph控制还是由发生塑性破坏时的压力值ex−df控制。因此可以得出以下的结论：1) 对于给定的土体，都存在一个临界深度，如图6所示。不同深度时的上抬力uph和发生塑性破坏时的压力值ex−df分别对应2条直线，这2条线的交点我们定义为临界深度，可以看出土体B-5的临界深度为3.6 m。这些线性关系可用于优化压密注浆的力学性能，尤其是在阶段性注浆的应用中。2) 对于浅注入(比临界深度浅)，注浆压力由上抬力uph控制。在这种情况下，注浆过程将由地表抬升控制。3) 对于深注入(比临界深度深)，注浆压力由土体发生塑性破坏时的压力值ex−df控制。在这种情况下，周围土体的强度和性能将得到改善，地面不会发生抬升。

图6 临界深度前后注浆压力的变化

4 结论

1) 将压密注浆过程视为理想土体中的球孔扩张问题，基于Mohr-Coulomb破坏准则，通过绕轴旋转将其破坏曲线改进为三维破坏模型，推导出单层土压密注浆压力及上抬力的计算模型，并给出详细求解方法和计算流程图。通过与EI-Kelesh等结果进行对比分析，证明了本文理论方法的正确性。

2) 采用MATLAB进行编程计算，分析了浆泡半径随注浆压力的变化规律，预测了不同土体在不同深度下的注浆压力值，同时还阐述了注浆压力随注浆深度的变化规律。

[1] Graf E D. Compaction grouting technique and observations[J]. Journal of Soil Mechanics and Foundations Division, 1969, 95(9): 1151−1158.

[2] Burland J B, Standing J R, Jardine F M, et al. Building response to tunneling, case studies from construction of the Jubillee line extention[M]. Thomas Telford, 2001.

[3] Bolton M D, Soga K, Jafari M R, et al. Soil consolidation associated with grouting during shield tunnelling in soft clayey ground[J]. Géotechnique, 2001, 51(10): 835−846.

[4] 冯旭海. 压密注浆作用机理与顶升效应关系的研究[D]. 北京: 煤炭科学研究总院, 2003. FENG Xuhai. A research on laws between the lift-effect and the mechanism of compaction grouting[D]. Beijing: China Coal Research Institute, 2003.

[5] Nicholson D P, Gammage C, Chapman T. The use of finite element methods to model compensation grouting [J]. Thomas Telford, 1994, 11: 297−312.

[6] Wisser C, Augarde C E, Burd H J. Numerical modelling of compensation grouting above shallow tunnels[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2005, 29(5): 443−471.

[7] 易小明, 张顶立, 逄铁铮, 等. 房屋注浆抬升实践与监测分析[J]. 岩土力学, 2009, 30(12): 3776−3782. YI Xiaoming, ZHANG Dingli, PANG Tiezheng, et al. Practice and monitoring analysis of building lifting due to grouting[J]. Rock and Soil Mechanics, 2009, 30(12): 3776−3782.

[8] Graf E D. Compaction grouting[J]. Geotechnical Special Publication, 1992, 30(1): 275−287.

[9] ZOU J F, XIA M Y. Uplift capacity of shallow anchors based on the generalized nonlinear failure criterion[J]. Mathematical Problems in Engineering, 2016:1−9.

[10] EI-Kelesh A M, Mossaad M E, Basha I M. Model of compaction grouting[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(11): 955−964.

[11] Vesic A S. Expansion of cavities in infinite soil mass[J]. Primary Care, 1973, 33(1): 75−91.

Study on determination method of pressure and uplifting force of compaction grouting of single-layer soil

CHENG Xuesong1, FAN Honghao1, ZHEN Xingwei1, LIU Lu2

(1. Quzhou Communications Investment Group, Quzhou 324100, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

Considering the three-dimensional conical shear failure of the soil during the grouting process, further study on the method of determining the pressure and lifting force of the single-layer soil compaction grouting has a particularly obvious guiding effect on engineering practice. In this paper, the spherical hole expansion model and the three-dimensional model of conical shear failure were used to study the mechanism of reinforcement of soil compaction grouting. The compaction grouting process was regarded as the problem of expansion of the spherical cavity in the ideal soil. Based on the Mohr-Coulomb failure criterion, the failure curve was developed into a three-dimensional curved surface by rotating around the axis, and the pressure of soil compaction grouting of the single-layer and the calculation model of the uplifting force are proposed. Compared with other people’s calculation results, the effectiveness of the method is verified.

single layer soil; compaction grouting; uplifting force; spherical hole expansion; three-dimensional damage

U45

A

1672 − 7029(2020)05 − 1162 − 09

10.19713/j.cnki.43−1423/u.T20190707

2019−08−07

国家科技重大专项资助项目(2017YFB1201200)

范洪浩(1981−)，男，浙江衢州人，高级工程师，从事港口海岸与近海工程研究；E−mail：2394870321@qq.com

(编辑 涂鹏)