基于Heston模型和遗传算法优化的铁路货运期权定价模型

冯芬玲，石昕

基于Heston模型和遗传算法优化的铁路货运期权定价模型

冯芬玲，石昕

(中南大学 交通运输工程学院，湖南 长沙 410075)

结合经济学理论，将期权理论引入货运定价，针对煤炭和钢铁等大宗型货物，运用Heston模型对铁路货运期权定价，设计改进型遗传算法拟合实际市场期权价格和Heston模型的期权价格的差值，优化模型参数，建立基于Heston模型和遗传算法优化的铁路货运期权定价模型，并运用上证50ETF买入期权数据对模型的参数进行优化，用广州局货运数据对算法进行验证，计算结果证明了算法的合理性，为铁路货运定价提供新思路。

铁路货运；Heston模型；期权定价；遗传算法

目前,货物运输市场竞争十分激烈，其中铁路一直负担着国民经济大动脉的作用，然而在大宗型货物运输市场有明显优势的铁路部门，近些年来的发展规模有逐步缩小的趋势，铁路货物运输竞争力不足。2014年至2016年，我国铁路货运量连续3年下滑，2016年全路货运量33.32亿t，相对于2015年下降0.8%，但在2018年，铁路货运量有了大幅提升达到40.30亿t。为了顺应运输市场需求，促进铁路货运业务积极参与运输市场竞争，自2013年以来，我国铁路货运运价改革逐步推进，如何科学理性地厘定合理的协议价格显得具有广泛的理论和实际意义。在铁路货运定价方法上的研究大致分为以成本为导向的定价方法和以需求为导向的定价方法2种。王哲[1]在对铁路运输企业成本定额指标体系法分类的基础上，为铁路运输企业应用成本定额方面提出了相应的改善建议。Comi等[2]对铁路运输定价的研究表明各运输需求主体的不同运输消费心理对应不同运价，为以需求为导向的差异定价奠定了理论基础。成本定价法考虑的重点是运输耗费的补偿，而需求导向定价更多以客户需求角度考虑市场供需平衡，现有的铁路货运定价方法难以适应当下运输定价要求，因此，结合铁路运力供给市场和契约市场将期权理论引入铁路货运定价，为铁路运输企业提供合理的定价思路。目前关于期权定价方面学者的研究主要包括Black-Scholes期权定价模型、Stackelberg博弈模型、二叉树法和Heston期权定价模型。Black等[3]提出了BS期权定价模型对标期权进行定价；Dempe等[4]提出基于双层数学规划的价格优化模型。二叉树法最早由Cox等[5]提出，它用分叉的树枝来描述股票和期权价格波动只有向上和向下2个方向。Heston模型是由Heston[6]提出的描述标的资产波动率变化的数学模型。Heston模型是一个随机波动模型，这种模型假设资产收益率的波动率跟随一个随机过程来运动。Henderson等[7]利用Girsanov变换将P测度转成Q测度进而分析Heston模型下的欧式期权定价问题。邱虹[8]借助Heston模型，通过矩匹配法和蒙特卡洛仿真法进行期权定价。在对Heston模型中的参数进行估计时，王林等[9]采用模拟退火算法并利用最小残差平方和来估算模型中的待估参数。李斌等[10]利用遗传算法能够进行群体搜索的特点，对参数的估计进行组合优化。张丽娟等[11]采用Heston模型，通过神经网络来拟合实际市场期权价格和Heston模型的期权价格的差值，并运用遗传算法来优化整个神经网络。已有的研究在Heston模型验证中数据大多假设而来，缺乏一定现实性，Heston模型相较于其他期权定价模型优势主要在于其假设波动率服从布朗运动，这更符合市场实际情况，且给出了闭式解。目前我国对铁路货运期权研究与应用较少，且在铁路货运期权定价方面，多采用BS定价模型、二叉树法等，Heston模型相较于其他模型主更具有灵活性，更符合实际情况，且目前货运期权交易大多凭借自身经验，具备货运期权交易的机构较少。本文借鉴金融领域的实物期权定价模式，引用Heston模型，设计改进型遗传算法对模型中的参数进行优化，在实证研究中，结合我国权证市场的真实交易数据和货运数据，对模型进行了验证，为铁路运输企业在货运定价方面提供参考。

1 铁路货运期权理论概述

期权，指一种合约，该合约赋予持有人在某一特定日期或该日之前的任何时间以约定的价格购进或售出一种资产的权利，该日期过后，合约失效。铁路货物运输中运费的波动影响着铁路企业、货主等多方收益，为合理规避双方所承担的风险，根据金融领域中期权的概念，结合铁路货物运输市场特点，可定义铁路货物运输期权如下。

1.1 铁路货运期权的概念

本文提出的铁路货运期权是指以铁路货物运输服务(货物运输运力)为标的资产的期权合约[12]，该合约赋予期权持有人(货主)在约定的到期日以约定的价格购进标的资产的权利。铁路运输企业作为期权的出售方，货主作为期权的买家，也就是合约持有人，享有履行合约的权利但不承担相应的 义务。

1) 标的资产：指选择购买或出售的资产，本文指货主购买的铁路货物运输服务，即货运运力。

2) 期权价格：期权的销售价格。

3) 期权执行价格：在期权合约中约定的、期权持有人据以购进标的资产的固定价格。

4) 到期日：期权合约中双方约定的期权到期日，该日买家可根据现货市场运价和期权执行价格来决定是否行使到期期权。

1.2 铁路货运期权交易流程

本文假设铁路运输企业和期权客户均为理性经济人，两者都希望在运输市场竞争和不确定条件下实现自身利益最大化。根据上述铁路货运期权定义，引入期权理论后，铁路运输企业需根据实际市场情况，制定合理的期权定价方案，而货主作为期权的买家则需根据运输企业公布的期权方案决定自身的购买方案，待期权到期后，根据市场价格，决定是否执行期权并支付执行费用。如图1。

图1 期权交易流程图

2 Heston模型及模型参数的估计优化

期权中资产收益的波动率是一个动态过程，Heston模型假设资产收益率的波动率并不恒定，而是跟随一个随机过程来运动，弥补了BS期权定价模型中假设标的资产的波动率为常数的不足，这样的假设更符合市场实际情况[13]。并且相较于其他随机波动率模型，Heston模型更易处理且为闭式解。

2.1 Heston模型

1993年，Heston根据CIR利率模型，提出资产价格波动遵循如下规律的假设：

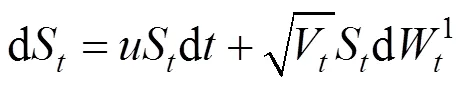
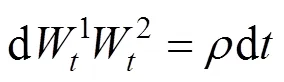
基于以上假设，可以得出＜时欧式看涨期权价格的闭式解：

这里：

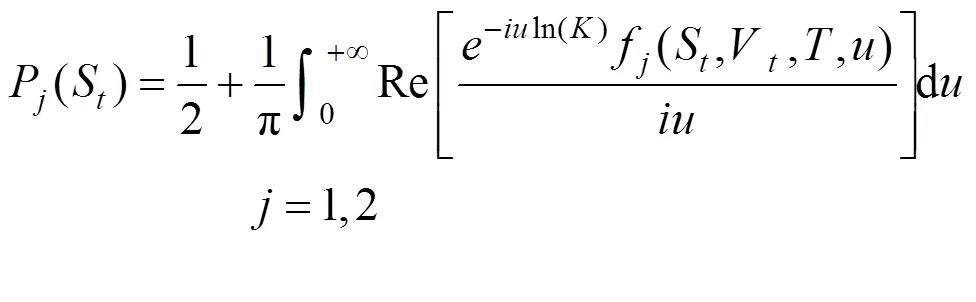
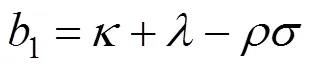
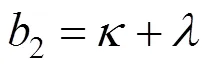
其中：1=0.5，2=−0.5，和表示欧式标准期权的执行价格和到期日；表示年利率；表示波动率风险的市场价格。

2.2 模型参数的估计优化

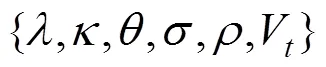
1) 编码及初始种群生成

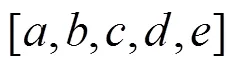
2) 选择

采用随机遍历抽样，依照个体的适应度值计算每个个体在子代中出现的概率，并按照此概率随机选择个体构成子代种群。

3) 交叉与变异

交叉方式采用双亲双子法，产生一个随机位，交换该随机位之后的所有基因，产生2个新的子代。变异方式采用实值种群变异。

4) 参数选择(交叉概率、变异概率、种群规模)交叉率和变异概率的改进[14]：基于Sigmoid函数和高斯分布函数对交叉率和变异率进行改进，设计自适应非线性调整交叉率和变异率的调节公式。

交叉率和变异率调节公式具体如下：

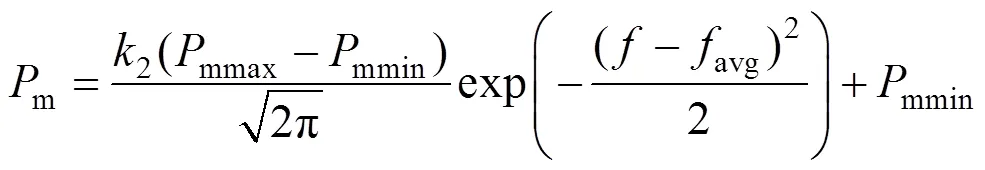
式中：avg表示种群的平均个体适应度；min表示种群中最小的个体适应度；max表示种群中最大的个体适应度；′表示要交叉的2个个体中较大的适应度；1为曲线平滑参数，取0.990；2表示曲线高度参数，取0.3；cmax和cmin表示交叉概率的最大和最小值；mmax和mmin表示变异概率的最大最小值。

2.3 Heston模型期权定价的步骤

将本文所采用的研究方法进行梳理，归纳出通过Heston模型来进行期权定价的步骤如下。

1) Heston模型参数估计数据的选取

本文选取上证50ETF期权数据来对Heston模型参数进行优化，假设上证50ETF期权市场与铁路货运期权市场波动一致。由于目前铁路货运权证市场尚处于理论研究阶段，未有真实期权价格数据，为了模型验证严谨且具有现实意义，选取上证50ETF，其是中国大陆期权交易市场唯一期权产品，交易较为活跃，相较于国外以及香港等交易所数据，大陆期权交易市场的波动更为贴合大陆铁路货运期权市场，使研究更具可靠性。

此外，在期权市场交易中，影响期权价格因素除了行权价格、无风险利率和到期时间外还与波动率紧密相关，这里重点探讨与期权价格波动关联最为密切标的资产的波动率。Heston模型假设标的资产及方差波动率遵循布朗运动，在现代金融数学领域中，普遍假设证券期货价格具有随机性特征。本文所探讨的铁路货运权证市场是证劵期货市场的一种，假设铁路货运期权中标的资产及方差波动率也遵循布朗运动，其变化也是一个随机过程，进而在实证研究中，选取证券交易市场真实期权数据对模型参数进行优化。

2) 货运数据的处理

按照《铁路货物运输品名分类与代码表》对不同货物品类分类，查询相应到发站之间的里程，根据下式对查询到的铁路货运数据进行处理，得到铁路货物运输价格c：

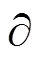
3) 运用本文提出的改进型遗传算法优化Heston模型中的5个参数。

4) 利用已求得的5个参数结合实际铁路货运数据，由式(17)计算得到的铁路货物运输价格c，回代至Heston模型中求出铁路货运期权价格。

3 实证研究

选取上海证券交易所50ETF指数在2019年4月1日的欧式买入期权交易记录为样本，期权到期日分别为4月12日、5月24日和6月23日，在样本的基础上利用Matlab软件编写对应的遗传算法程序，经计算得到Heston模型中的待估参数。

再分别以4月1日长沙北发往娄底东、株洲北和广州东3个货运站，煤球、矿石等大宗型货物运输期权为例，假设期权合约有效期限为1个月，利用相关运输数据和已得到的待估参数，对铁路货运期权进行预测定价。

3.1 样本数据

2019年4月1日上证股指收盘价是2.906，无风险利率选取1年期中债国债收益率是0.026 902[15]。样本数据见表1。

表1 上证50ETF买入期权样本数据

3.2 实证分析

3.2.1 参数估计结果与分析

针对2019年4月1日买入期权的样本，遗传算法上设定进化代数为350初始种群规模为80，得到估计的参数为：[V,,,,]=[0.070 37, 6.479 641, 0.068 934, 0.448 885, 0.393 213]，此时适应度最优值为1.75×10−5。图2为进化过程中种群各代最优适应度值变化趋势。

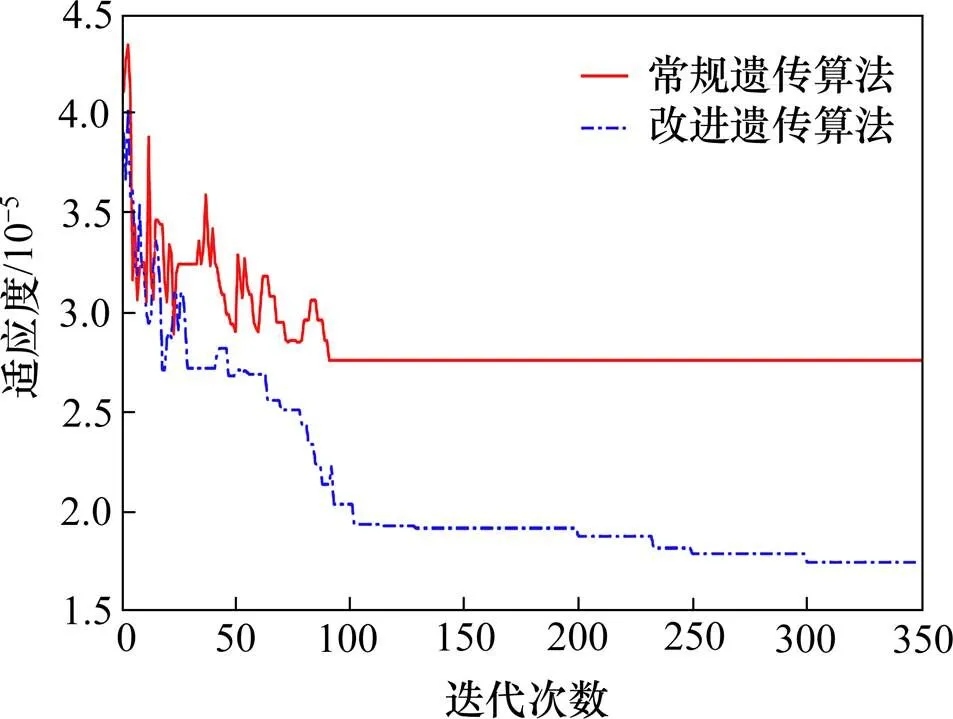
图2 种群最优个体适应度趋势

从图2可以看出，由于本文分别对交叉概率和变异概率按个体适应度以Sigmoid函数曲线和高斯分布曲线形式进行了优化，在进化初期种群最优适应度值震荡较为剧烈，但在50代之后各代最佳个体适应度值呈现严格的递减趋势，避免了迭代过程中算法收敛速度变慢和局部最优的可能。

在遗传算法运算100次之前，最佳个体适应度值收敛得非常快，尤其在运算50次之前，种群最优适应度值的波动剧烈，达到100次左右时，种群最优适应度值的波动愈来愈小，并且呈现递减的趋势，在100~300次运算最佳个体适应度值仍呈现收敛的趋势，最终在350次运算后最佳个体适应度值稳定在1.75×10−5，从种群层面看具有收敛性。从图2可以看到，算法经常跳出局部极小值，这说明本文采用的改进型遗传算法求得的Heston模型中的5个待估参数，随着迭代次数的增加越来越优，体现了本文算法的寻优性。

3.2.2 期权定价结果

把上文采用遗传算法运算所得到的Heston模型参数，结合收集到的铁路货运数据应用于期权定价中。由于货运品类多样化，按照货物品类来设计多种期权不符合实际，在真实权证市场中，也是按照大类划分，因此实例分析中参考真实权证市场将各品类货物按类别划分定价。

表2 大宗型货物运输价格样本数据

表2收集了2019年4月1日，7种类别，3个到站的铁路货运整车价格运输数据，由于广州东和株洲北站为特等站，娄底东为3等站，分别对其赋予权重0.4，0.4和0.2，据式(17)计算出相应类别货物运输价格，假设期权到期时间为1个月，利用Heston模型对期权定价结果如表3。

经模型运算得出对应种类货物期权价格，期权客户通过购买此看涨期权，获取在未来1个月时间内以约定的价格购买一定运力的权限，运输企业必须提供相应运力。同样货主也可根据市场价格情况选择放弃执行期权，但会损失已付出的期权费用，运输企业失去客源但获得了相应的期权购买收入，在一定程度上弥补了损失，且在货主放弃行使期权时，运输企业有足够时间更新销售计划安排剩余运力。

表3 Heston模型期权定价结果

与表2中铁路货物运输价格相较，货主只需付出较少的期权费用即可获得运力保证，铁路运输企业也可获得相应期权收益，这是双方受益的一种定价方式。从模型算法上看，本文采用改进型遗传算法来估计Heston模型参数，解决了Heston模型闭式解形式比较复杂，参变量多的特点，在一定程度上提升了算法的寻优性。从实证结果上看，基于上证期权交易数据，对模型参数进行估计，结合实际货运数据应用到期权定价中去，证明Heston模型对铁路货运定价是有效、可行的。

目前我国铁路运输市场中，铁路运输企业与货主签订提前运输协议来销售一部分运力，此类运输协议的签订对于交易稳定性较差的现货市场在稳定货源及运力方面有一定优势，一方面为运输企业提供稳定大宗货源，另一方面为货主提供稳定运力，也有效避免了由于铁路货运价格市场的波动为双方带来的损失。在运输企业与货主之间，引入期权金融工具，是实现铁路公司与客户实现双赢的方式，我国应制定灵活定价策略，科学管控期权等金融衍生品风险，丰富与完善铁路货运定价体系，提高铁路运输效率，提升铁路竞争力。

4 结论

1) 运用金融工程等学科知识构建基于Heston模型的铁路货运期权定价模型，研究所设计铁路货运期权的最优定价决策。结果表明，Heston模型可用于对铁路货运权证市场进行分析；在优化模型参数上，所设计的改进型遗传算法无论在收敛速度还是稳定性上都有较为明显的提升；用我国权证市场的真实交易数据和铁路货运市场数据对Heston模型的实证，也检验了模型的可行性和有效性。

2) 本文提出的改进型遗传算法有效把握了总体的进化方向，同时按个体适应度使用Sigmoid函数和高斯函数自适应的调整交叉概率和变异概率，实验结果表明改进的遗传算法无论在收敛速度还是稳定性上都有较为明显的提升。

3) 研究成果可对铁路运输企业在铁路货运市场化运营过程中的运价改革提供参考依据，但我国目前在铁路货运期权方面尚处于理论研究阶段，本文研究侧重于期权价格的确定，今后可针对期权执行价格和购买数量等进行更加详细、深入的研究。

[1] 王哲. 铁路运输企业成本定额指标体系应用困境及对策研究[D]. 北京: 北京交通大学, 2014. WANG Zhe. Research on the problem and the countermeasures of railway transport enterprise cost quota index system[D]. Beijing: Beijing Jiaotong University, 2014.

[2] Comi A, Coppola P, Nuzzolo A. Freight transport modeling: Review and future challenges[J]. Rivista Internazionale di Economia dei Transporti/International Journal of Transport Economics, 2013, XL(2):151−181.

[3] Black F, Scholes M. The effects of dividend yield and dividend policy on common stock prices and returns[J]. Journal of Financial Economics, 1974, 1(1): 1−22.

[4] Dempe S, Bard J F. Bundle trust-region algorithm for bilinear bilevel programming[J]. Journal of Optimization Theory & Applications, 2001, 110(2): 265−288.

[5] Cox J, Ross S, Rubinstein M, et al. Option pricing: A simplified approach[J]. Journal of Financial Economics, 1979, 7(3): 229−263.

[6] Heston S L. A closed-form solution for options with stochastic volatility with applications to bond and currency options[J]. Review of Financial Studies, 1993, 6(2): 327−343.

[7] Henderson V, Hobson D, Howison S, et al. A comparison of option prices under different pricing measures in a stochastic volatility model with correlation[J]. Review of Derivatives Research, 2005, 8(1): 5−25.

[8] 邱虹. 基于Heston模型的能源商品定价机制研究[J]. 南华大学学报(社会科学版), 2018, 19(1): 82−87. QIU Hong. Research on energy commodity pricing mechanism based on Heston model[J]. Journal of University of South China (Science and Technology), 2018, 19(1): 82−87.

[9] 王林，张蕾，刘连峰.用模拟退火算法寻找Heston期权定价模型参数[J]. 数量经济技术经济研究, 2011(9): 131−139. WANG Lin, ZHANG Lei, LIU Lianfeng. Calibration of Heston’s option pricing model by using simulated annealing algorithm[J]. The Journal of Quantitative & Technical Economics J Quant Tech Econ, 2011(9): 131− 139.

[10] 李斌, 何万里. 一种寻找Heston期权定价模型参数的新方法[J]. 数量经济技术经济研究, 2015(3): 129−146. LI Bin, HE Wanli. A new method of finding the parameteters of Heston’s option pricing model[J]. The Journal of Quantitative & Technical Economics J Quant Tech Econ, 2015(3): 129−146.

[11] 张丽娟, 张文勇. 基于Heston模型和遗传算法优化的混合神经网络期权定价研究[J]. 管理工程学报, 2018, 32(3): 142−149. ZHANG Lijuan, ZHANG Wenyong. Option pricing model by applying hybrid neural network based on Heston model and genetic algorithm[J]. Journal of Industrial Engineering/Engineering Management, 2018, 32(3): 142−149.

[12] 冯芬玲, 李菲菲. 基于期权理论的铁路货运定价模型[J]. 铁道科学与工程学报, 2012, 9(2): 72−78. FENG Fenling, LI Feifei. Pricing model of railway cargo transport based on option theory[J]. Journal of Railway Science and Engineering, 2012, 9(2): 72−78.

[13] 白薇. 拟蒙特卡洛方法下Heston模型的离散化[D]. 北京: 清华大学, 2015. BAI Wei. Discretizations of Heston model under Quasi- Monte Carlo method[D]. Beijing: Tsinghua University, 2015.

[14] 王嵘冰, 徐红艳, 郭军. 自适应的非支配排序遗传算法[J]. 控制与决策, 2018, 33(12): 82−87. WANG Rongbing, XU Hongyan, GUO Jun. Adaptive non-dominated sorting genetic algorithm[J]. Control and Decision, 2018, 33(12): 82−87.

[15] 陈紫薇. 基于Heston随机波动模型的上证50ETF期权定价与对冲研究[D]. 大连: 大连理工大学, 2016. CHEN Ziwei. Research of pricing and hedging of the SSE 50ETF option based on Heston stochastic volatility model[D]. Dalian: Dalian University of Technology, 2016.

Option pricing model by railway cargo transport based on Heston model and genetic algorithm

FENG Fenling, SHI Xin

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

With the increasingly fierce competition in the railway freight market, it is urgent to construct a freight pricing method that will help improve railway transportation efficiency and market competitiveness. This paper combined economic theory and introduced the concept of option theory into freight pricing. For large-scale cargo such as coal and steel, Heston model was used to price railway freight options, and then used improved genetic algorithm to fit the market option price and the option price of the Heston model. The option pricing model was constructed based on Heston model and genetic algorithm, using the SSE 50ETF buy option and the Guangzhou Railway Group freight data to verify the algorithm. The calculation results prove the rationality of the algorithm, and the algorithm provides a new idea for railway freight pricing.

railway freight transport; Heston model; option pricing; genetic algorithm

U2-9

A

1672 − 7029(2020)05 − 1295 − 07

10.19713/j.cnki.43−1423/u.T20190858

2019−09−25

国家社会科学基金资助项目(18BJY169)

冯芬玲(1973−)，女，河北邯郸人，教授，博士，从事铁路货物运输、运输市场营销研究；E−mail：ffl0731@163.com

(编辑 阳丽霞)