地铁列车运行时引起的隧道内振动荷载研究

黄强，刘干斌，万灵，朱瑶宏，黄宏伟

地铁列车运行时引起的隧道内振动荷载研究

黄强1，刘干斌1，万灵2，朱瑶宏1，黄宏伟3

(1. 宁波大学 岩土工程研究所，浙江 宁波 315211；2. 江西农业大学 工学院，江西 南昌 330045；3. 同济大学 地下建筑与工程系，上海 200092)

地铁环境振动研究首先需要确定隧道内的振动荷载。针对以往采用的解析计算模型确定地铁振动荷载时对列车、轨道、地基各子模型的影响研究不够，基于车辆−轨道−隧道−地基模型对此进行详细分析。研究结果表明：不考虑轨道不平顺时，列车可以直接简化为移动点荷载，考虑轨道不平顺时，不同列车模型确定的地铁振动荷载差别不大，但轮轨力存在一定差异，列车最好采用整车模型。整体式轨道的地铁振动荷载最大，有砟轨道次之，浮置板轨道最小。浮置板可以有效减少地铁振动荷载的幅值和频率，但随着浮置板长度增加振动荷载趋于恒定。地基模型对地铁振动荷载影响很小，地基可直接简化为Winkler模型。对计算模型中不同子模型的影响进行分析，可为地铁振动荷载的确定提供一定的参考。

地铁振动荷载；列车模型；轨道类型；地基模型；轨道不平顺

随着地铁线路增多和地铁线路与周围建筑物的距离不断减小，地铁列车运行引起的环境振动日益受到大家的关注。对于地铁环境振动分析，通常采用“两步走”的策略，首先是采用理论模型确定隧道内的振动荷载，然后建立隧道−地基有限元模型进行动力数值计算。由此可见，地铁振动的首要问题是确定隧道内的地铁振动荷载。地铁振动来自于轮轨的相互作用，地铁振动除了与车辆、轨道结构参数有关外，还与隧道、地层的特性也相关，因而，合理的荷载计算模型应该反映车辆、轨道、隧道、地基各子系统的综合影响。对于地铁振动荷载，不同学者采用的荷载形式有所不同。有的学者直接把轮轨接触力视为地铁振动荷载，不考虑轨道系统对轮轨力的传递作用，将轮轨力直接简化为移动点荷载或移动简谐荷载[1−2]，这种做法通常会夸大列车振动作用，并不十分合理。大多数学者采用不同力学计算模型来确定地铁振动荷载。例如，翟婉明[3]首先提出了车辆−轨道垂向系统统一模型，列车简化为10自由度的整车模型，轨道为三层连续梁−质量模型。XIA等[4]也采用类似的荷载计算模型计算了隧道道床上的振动荷载，以此作为后续地铁振动响应数值计算的荷载输入条件。还有学者进一步考虑了隧道和地基的影响，采用车辆−轨道−隧道−地基模型确定作用在隧道上振动荷载，如XU等[5]利用车辆−轨道−隧道−地基纵向模型计算了整体式轨道和浮置板轨道下隧道结构上的振动荷载时程，并对地铁运行的二维和三维地铁振动响应进行对比。此外，王田友等[6]也利用该计算模型计算了隧道道床上的振动荷载，认为钢轨−隧道−地基纵向模型得到荷载时程适用于三维地铁环境振动分析。事实上，选择哪个层面上振动荷载作为地铁振动荷载取决于所建立模型的精细程度，轨道层数越多，传递到隧道上的振动荷载将变得不同。为减少后续隧道−地基有限元模型动力计算的工作量，采用“两步走”策略时学者们通常把作用在隧道道床上的振动荷载作为地铁振动荷载，本文也采用同样的考虑。如前面所述，车辆−轨道−隧道−地基纵向模型作为地铁振动荷载计算模型被广泛采用。该计算模型可以充分反映列车、轨道、隧道、地基等诸多子模型因素的影响，但是，对于该理论计算模型中各子模型选择差异带来的影响，以往的分析则较少涉及。譬如，列车可以简化为整车模型、1/4列车模型、移动点荷载等多种情况；轨道类型又有整体式轨道、浮置板轨道、有砟轨道等多种类型；地基模型也可分为Winkler地基、Pasternak地基、Kerr地基3种情况。在以往的荷载解析计算模型中，子模型的选择具有一定的主观随意性，各子模型对地铁振动荷载的影响较少进行专门的研究。有鉴于此，本文基于车辆−轨道−隧道−地基纵向模型，首先对各子模型的影响进行单独分析，指出各子模型的差异及相应的适用条件，最后，比较轨道不平顺条件下浮置板轨道和整体式轨道下的地铁振动荷载差异。本文的研究可为地铁振动荷载计算模型的选择提供一定的参考。

1 列车模型影响

单节列车可以简化为3种典型的列车模型：10自由度整车模型[3]、1/4列车模型[7](二系悬挂)、移动点荷载模型[1]。不同列车简化模型下的车辆−轨道−隧道−地基计算模型如图1所示，车辆类型为上海地铁标准A型车，钢轨为60号重轨，DTVI2型扣件，轨道为整体式道床轨道，钢轨、隧道都简化为离散支承的Euler长梁，间距0.60 m，地基简化为离散支承的Winkler地基，弹性模型为50 MPa，为中压缩性地层。通过弹性空间法换算的基床系数为3.33×106N/m3。图1模型的参数如表1所示，地铁隧道抗弯刚度考虑环向接缝的影响，纵向抗弯刚度取隧道衬砌圆环的1/7[8−10]。在分析列车模型的影响时，需考虑钢轨不平顺存在与否2种情况。由于地铁移动速度一般不大(<80 km/h)，可认为轮轨始终处于接触状态。采用振动叠加法和Runger-Kutta法对图1各模型动力方程进行求解。振型叠加法中模型计算长度为420 m，梁的模态数设为400，通过试算可以满足计算要求。

(a) 整车模型；(b) 1/4列车模型；(c) 移动点荷载模型

1.1 不考虑轨道不平顺情况

采用整体式道床轨道时，扣件反力即为隧道上的振动荷载。不考虑轨道不平顺情况时，3种列车模型下的扣件反力如图2所示。可以看出，3种列车模型下的地铁振动时程曲线一致，荷载峰值也十分接近，分别为31.77，32.09和31.50 kN。由此可见，不考虑不平顺时，不同列车模型得到的地铁振动荷载几乎一致，列车完全可以简化为移动点荷载，从而减少计算量。

表1 车辆-轨道-隧道-地基模型参数

图2 不考虑轨道不平顺时扣件反力对比

另外，比较钢轨挠度和隧道挠度，不同列车模型下的计算结果也近乎一致，其原因是钢轨挠度与隧道挠度主要受地基刚度的影响，与列车模型选择关系不大。钢轨挠度在列车经过时出现了快速升起下降现象，呈现明显的峰值，但隧道挠度没有出现这种脉冲的现象，单节列车驶过时只有一个挠峰值度。一个值得注意的地方是，由于考虑了隧道结构存在，且隧道结构刚度要比轨道结构大得多，导致钢轨与隧道的变形范围较大，从图2中可看出，影响范围可超过100 m。

1.2 考虑轨道不平顺情况

单涛涛等[9]对上海地铁1号线的轨道高低不平顺进行研究，认为上海地铁1号线的轨道不平顺谱介于美国5级和6级轨道不平顺谱之间。本文以美国5级轨道不平顺谱为例，分析轨道不平顺对地铁振动荷载的影响，首先得到美国5级轨道不平顺时程曲线如图5所示。

图3 不考虑轨道不平顺钢轨挠度时程对比

图4 不考虑轨道不平顺隧道挠度时程对比

图5 轨道不平顺时程(美国5级轨道谱)

图6 考虑轨道不平顺时轮轨接触力时程对比

首先得到列车移动时的轮轨力，截取稳定阶段的轮轨力变化时程，如图6可以看出，考虑轨道不平顺后整体列车模型和1/4列车模型的轮轨力在列车自重荷载上下波动，1/4列车模型的轮轨力最大，整车模型次之，移动点荷载的轮轨力最小，幅值分别为85.04，82.08和77.25 kN。可见，考虑轨道不平顺时，1/4列车模型会高估轮轨接触力，而移动点荷载模型会低估，列车此时简化为整车模型更为合理。不过，由于地铁列车的运行速度不大(20 m/s左右)，不同列车模型之间的轮轨力差距不大，最大约8 kN左右。再比较隧道上的振动荷载，如图7所示，3种列车模型下的扣件反力分别为33.20，32.09和31.50 kN，仅有轻微的差异。可见，即使考虑了轨道不平顺，传递至隧道上的地铁振动荷载仍然差别不大，说明轨道不平顺对地铁振动荷载的影响实际不大。

图7 考虑轨道不平顺时扣件反力时程

2 轨道模型的影响

地铁轨道结构可分为整体式轨道、浮置板轨道和有砟轨道，整体式轨道模型如图1(c)所示，有砟轨道和浮置板轨道如图8所示。列车视为移动点荷载，浮置板视为短梁，道砟视为质量块。计算长度仍取420 m，轨道离散支承，仍选取轨道中部位置响应进行分析。浮置板基本参数如表2所示，其余参数参考表1。

表2 浮置板轨道计算参数

比较不同轨道模型下的钢轨挠度，如图9所示，不同轨道模型的钢轨挠度时程类似，在列车经过时产生都会产生明显的脉冲现象。然而，有砟轨道和浮置板轨道的钢轨挠度峰值要比整体式轨道大得多，分别为5.37，5.14和1.67 mm。不同浮置板长度下的钢轨挠度如图10所示，有砟轨道的钢轨挠度最大，浮置板次之，整体式轨道的挠度最小。随着浮置板长度的增加浮置板轨道的钢轨挠度逐渐减少，最终趋于稳定，但仍比整体式轨道大得多。可见，当轨道层数增多，轨道结构的整体刚度就越小，钢轨的挠度就越大。不过，3种轨道结构下的隧道挠度近乎一致，表明轨道类型变化对下卧隧道挠度的影响很小，这是因为隧道挠度主要受下卧地基刚度的影响，与轨道类型关系不大。

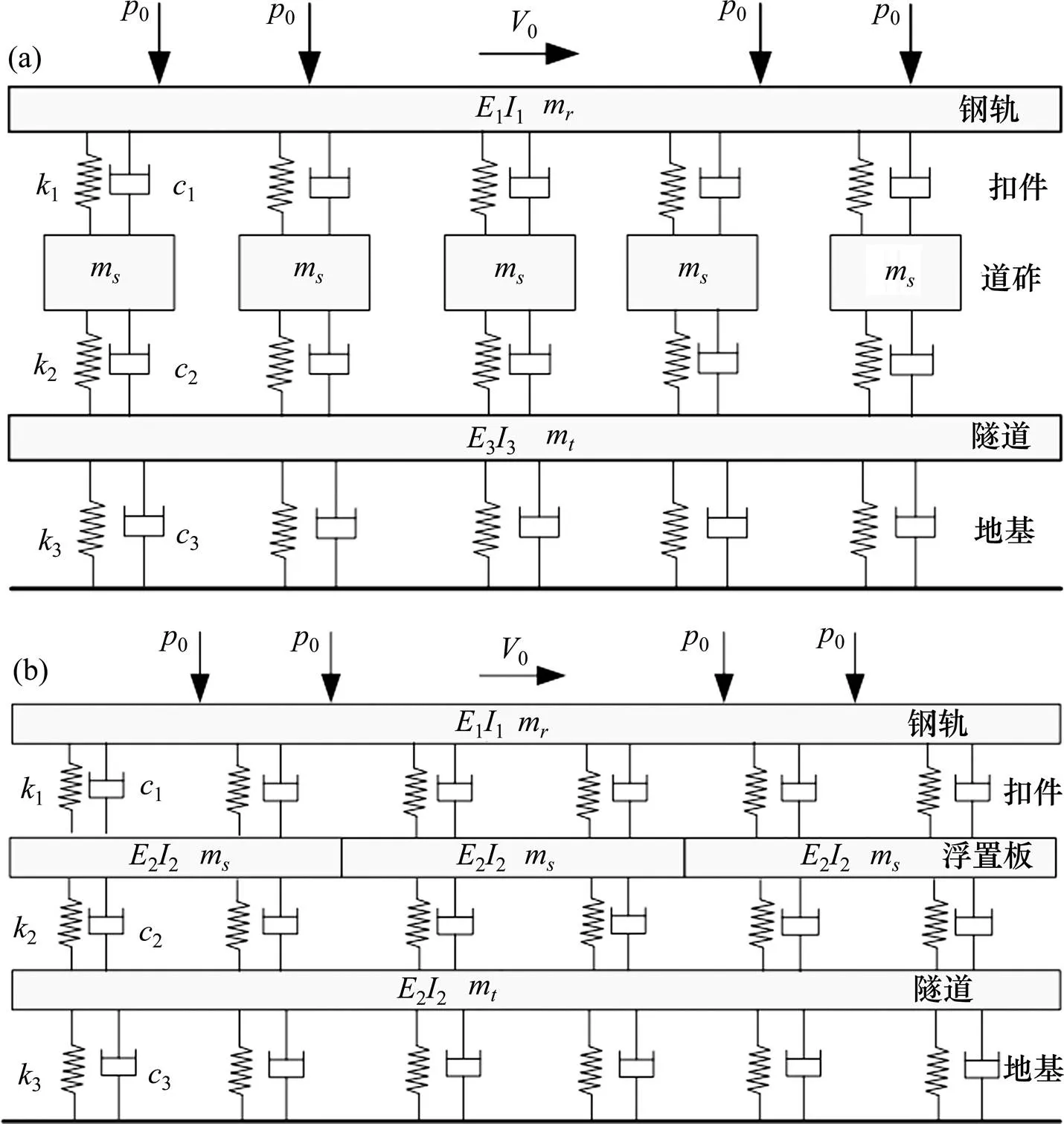
(a) 浮置板轨道模型；(b) 有砟轨道模型

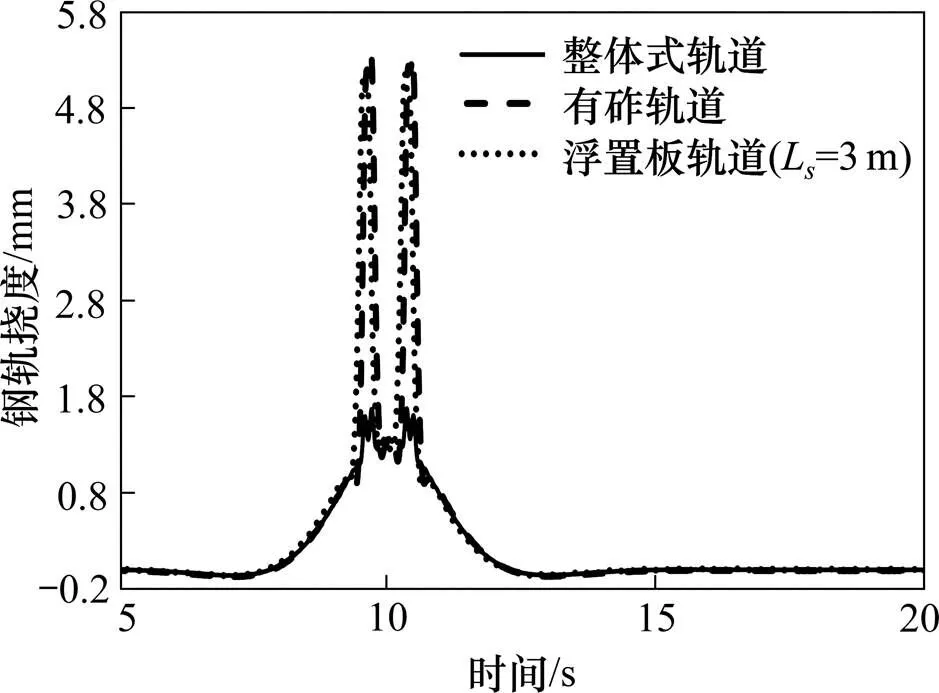
图9 不同轨道结构下钢轨位移对比

图10 不同浮置板长度下钢轨挠度

再比较扣件反力，如图12所示，可知有砟轨道的扣件反力最小，浮置板轨道的扣件反力则随浮置板长度增加先增加，随后随着浮置板长度增加荷载有所波动，但最终与整体式轨道得到的计算结果接近。

图11 不同轨道结构下隧道挠度对比

图12 不同浮置板长度下钢轨扣件反力对比

隧道上的振动荷载才是本文的关注点，如图13所示，不同轨道形式下的隧道荷载时程曲线有所不同，整体式轨道下的地铁振动荷载最大，且时程曲线呈现出明显的脉冲现象，有砟轨道和浮置板轨道的荷载峰值明显减少且只有2个波峰。进一步比较3种轨道模型下的隧道振动荷载差异，从图14中可以看到，采用浮置板轨道下的地铁振动荷载幅值最小，其次是有砟轨道，而整体式轨道的地铁振动荷载最大。随着浮置板浮置板长度增加，隧道上的振动荷载不断减少，当浮置板长度达到一定长度时，隧道振动荷载幅值也趋于稳定。

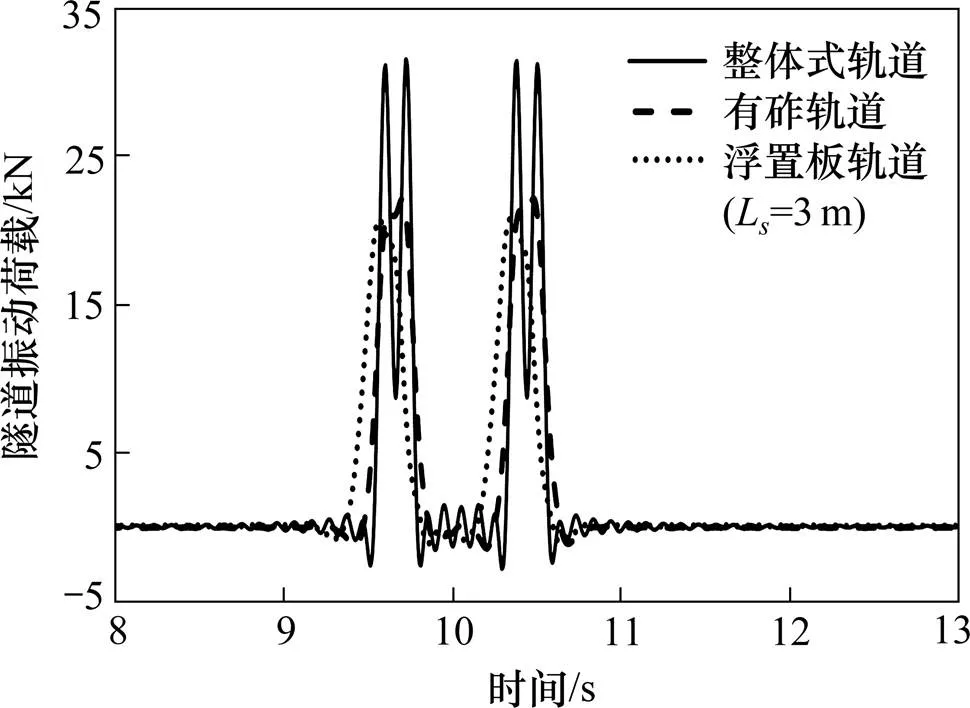
图13 不同轨道模型下隧道上振动荷载时程对比

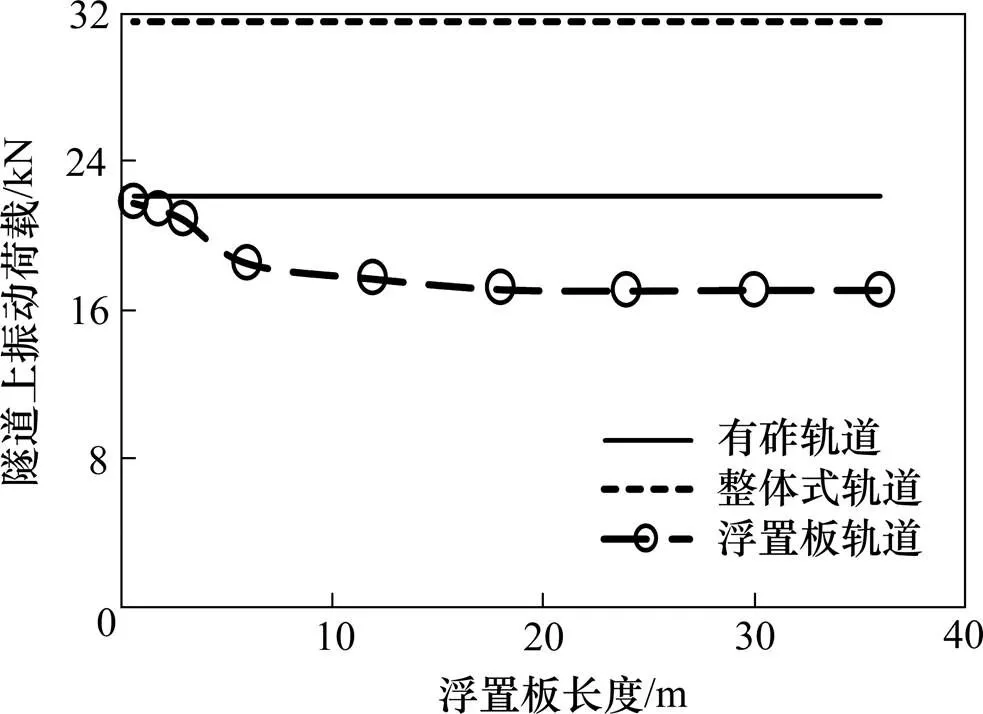
图14 不同浮置板长度下隧道振动荷载

3 地基模型影响

在地铁振动荷载计算模型中，还要考虑下卧地基的影响，常见的地基模型有Winkler地基[12]、Pasternak地基[13]、Kerr地基[14]3种，如图15所示。各地基模型的参数[15]可以通过弹性空间法换算确定，各地基模型的换算公式如下：

假设地基弹性模量为50 MPa，厚度为15 m，求得各地基模型参数如表3所示。为方便地基梁模型求解，弹性支承都考虑为连续支承情况，利用双重傅里叶变换和围道积分解析方法求解地基梁模型。

表3 不同地基模型参数

(a) Winkler地基；(b) Pasternak地基；(c) Kerr地基

图16 不同地基模型下的钢轨挠度对比

图17 不同地基模型下的隧道挠度对比

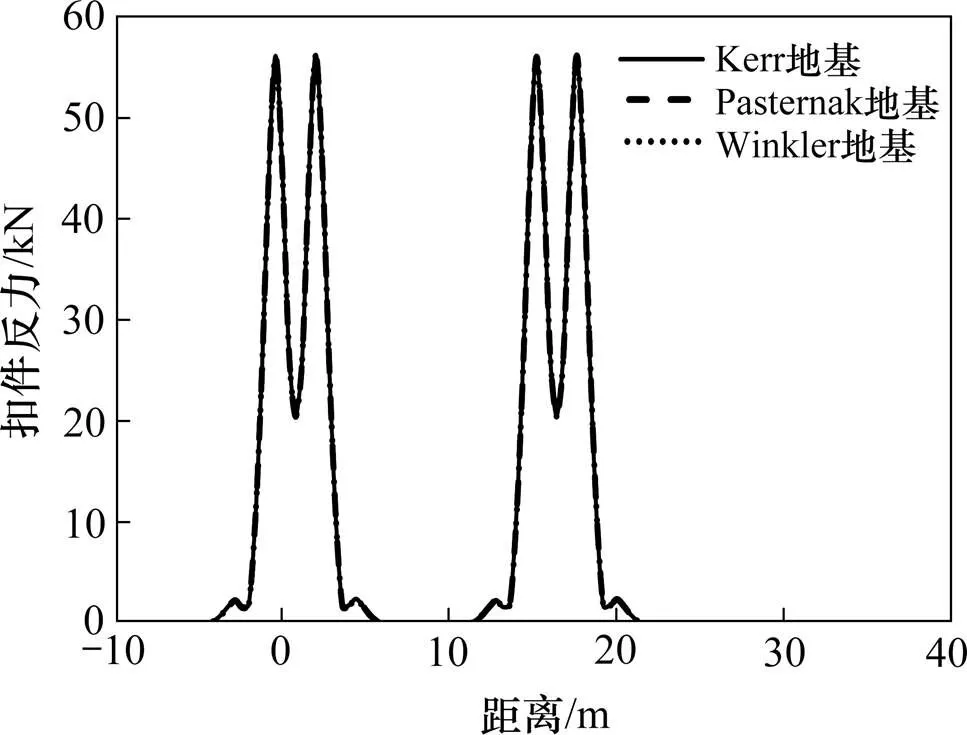
图18 不同地基模型下的扣件反力对比

subgrade models

不同地基梁模型的钢轨挠度、隧道挠度和扣件反力，如图16~18所示。从图16~18可看出，3种地基模型的计算结果基本一致，说明地基模型不同对隧道及轨道结构的挠度及振动荷载影响可忽略不计，采用弹性空间法换算得到各模型地基刚度其实差别不大。这个结论可能与文献[16]中的结论有所不同，两者差异的主要原因是此处考虑了隧道结构的存在，轨道结构不是直接作用在地基上，导致轨道以下的地基−隧道系统刚度较为接近。由于隧道抗弯刚度远大于轨道结构，使得下卧地基模型差异对上部轨道与隧道结构的挠度与内力影响很小。

4 多节编组列车地铁振动荷载计算

通过对车辆−轨道−隧道−地基模型中各子模型的影响分析，本文以上海地铁为例，计算多节编组列车运行时隧道内的振动荷载可作为地铁环境振动数值计算的输入荷载。仍考虑轨道不平顺为美国5级轨道谱的不利情况，轨道形式分别为整体式轨道和浮置板轨道(长度为3 m)。列车采用整车模型，模型参数与前面子模型一致，得到8节编组列车移动时作用在隧道上的振动荷载时程，如图19和图20所示。从计算结果看，2种轨道的地铁振动荷载时程曲线明显不同，整体式轨道下的荷载时程曲线呈现明显的脉冲现象，可以清楚看出车轮的移动过程，而浮置板轨道下的振动荷载幅值小得多，荷载波动也没有那么剧烈。再比较两者的频谱曲线，如图21所示，发现整体式道床轨道下的荷载主频在15 Hz以下，而浮置板道床的振动主频在5 Hz以下，说明浮置板轨道不仅可以有效减少隧道上的振动荷载幅值，也能降低荷载振动频率，从而起到良好的减振效果。

图19 整体式轨道下8节编组列车的地铁振动荷载

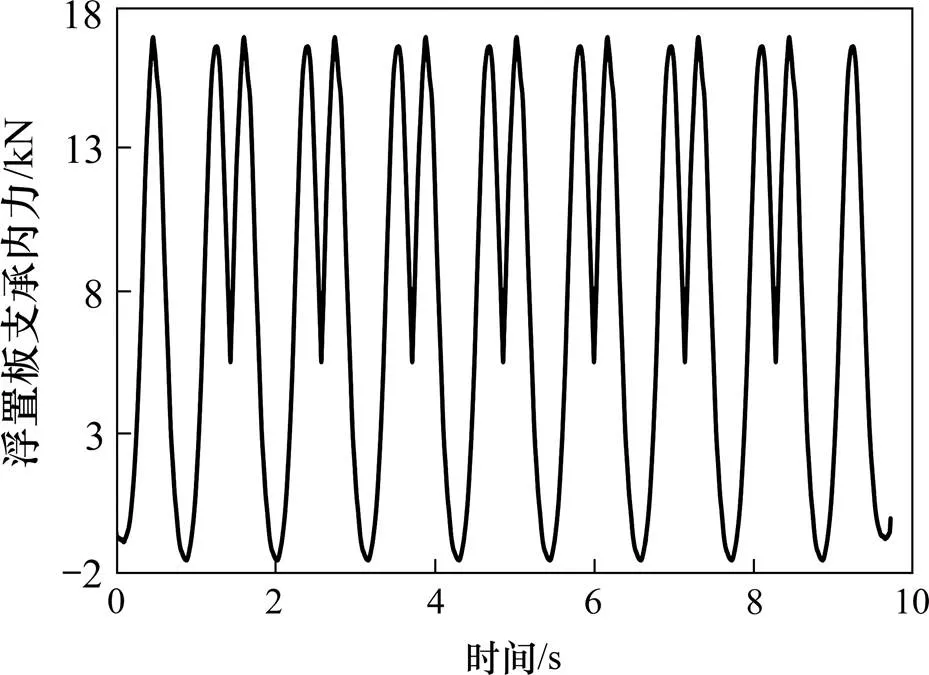
图20 浮置板轨道下8节编组列车的地铁振动荷载

图21 不同轨道形式下的振动荷载频谱对比

5 结论

1) 不考虑轨道不平顺时，不同列车模型得到地铁振动荷载近乎一致，列车可以直接简化为移动点荷载；考虑轨道不平顺时，1/4列车模型的轮轨力偏大，移动点荷载模型偏小，列车应简化为整车模型。不过，由于列车运行速度不大，轨道不平顺引起的轮轨力差异不明显，最终传递到隧道上的地铁振动荷载差别不大。

2) 轨道类型对钢轨挠度、扣件反力和隧道上的振动荷载有重要影响。整体式轨道的地铁振动荷载最大，有砟轨道次之，浮置板轨道最小。浮置板轨道可以有效减少隧道上的荷载幅值及主频，随着浮置板长度的增加，荷载逐渐减少并趋于恒定。

3) 地基模型对上部轨道和隧道变形与受力影响很小，这是因为隧道结构刚度远大于轨道结构，削弱了地基模型的影响，地基可以直接简化为Winkler模型。

[1] LU J F, DING J J, FAN Z, et al. Response of a circular tunnel embedded in saturated soil to a series of equidistant moving loads[J]. Acta Mechanica, 2017(228): 3675−3693.

[2] HE Chao, ZHOU Shunhua, GUO Peijun, et al. Modelling of ground vibration from tunnels in a poroelastic half-space using a 2.5D FE-BE formulation[J]. Tunnelling and Underground Space Technology, 2018(82): 211−221.

[3] 翟婉明. 车辆−轨道垂向系统的统一模型及其耦合动力学原理[J]. 铁道学报, 1992, 14(3): 10−21. ZHAI Wanming. The vehicle model of vehicle-track system and its coupled dynamics[J]. Journal of the China Railway Society, 1992, 14(3): 10−21.

[4] XIA H, Cao Y M, ZHANG N. Numerical analysis of vibration effects of metro trains on surrounding environment[J]. International Journal of Structural Stability and Dynamics, 2007, 7(1): 151−166.

[5] XU Q Y, XIAO Z C, LIU T, et al. Comparison of 2D and 3D prediction models for environmental vibration induced by underground railway with two types of tracks[J]. Computers and Geotechnics, 2015(68): 169− 183.

[6] 王田友, 丁洁民, 楼梦麟. 地铁运行引起场地振动的荷载与分析方法[J]. 工程力学, 2010, 27(1): 195−201. WANG Tianyou, DING Jiemin, LOU Menglin. Load for subway-induced free field vibration and analysis method[J]. Engineering Mechanics, 2010, 27(1): 195− 201.

[7] BIAN X C, JIANG H G, CHANG C, et al. Track and ground vibrations generated by high-speed train running on ballastless railway with excitation of vehicle track irregularity[J]. Soil Dynamics and Earthquake Engineering, 2015(76): 29−43.

[8] 徐凌. 软土盾构隧道的的纵向沉降[D]. 上海: 同济大学, 2006. XU Ling. Longitudinal settlement of shield tunnel in soft deposit[D]. Shanghai: Tongji University, 2006.

[9] 单涛涛, 楼梦麟, 贾宝印. 关于上海地铁一号线轨道高低不平顺问题的探讨[J]. 振动与冲击, 2012, 31(12): 53−58. SHAN Taotao, LOU Menglin, JIA Baoyin. Preliminary exploring a problem of track vertical profile irregularity of Shanghai metro line 1[J]. Journal of Shock and Vibration, 2012, 31(12): 53−58.

[10] 黄强. 地铁振动荷载下饱和软土隧道自由场响应与沉降研究[D]. 上海: 同济大学, 2018. HUANG Qiang. Free-field response and settlement of a metro tunnel in saturated soft ground subjected to train vibration load[J]. Shanghai: Tongji University, 2018.

[11] KUO M C, HUANG C H, CHEN Y Y. Vibration characteristics of floating slab track[J]. Journal of Sound and Vibration, 2008, 317(3−5): 1017−1034.

[12] Winkler E. Die lehre von elastizität und festigkeit (The Theory on elasticity and fixity)[M]. Prague: Dominicus, 1867.

[13] Pasternak P L. Fundamentals of a new method of analyzing structures on an elastic foundation by means of two foundation moduli[M]. Moscow: Gosudarstvennoe Izdatelstro Liberaturi po Stroitelstvui Arkhitekture, 1954.

[14] Kerr A D. Elastic and viscoelastic foundation models[J]. Journal of Applied Mechanics, 1964, 31(3): 491−498.

[15] Horvath J S. New subgrade model applied to mat foundations[J]. Journal of Geotechnical Engineering, 1983, 109(12): 1567−1587.

[16] 黄强, 黄宏伟, 张冬梅, 等. 移动简谐荷载作用下Kerr地基梁的稳态响应研究[J]. 振动与冲击, 2018, 37(1): 14−20. HUANG Qiang, HUANG Hongwei, ZHANG Dongmei, et al. Steady-state response of an infinite Euler-Bernoulli beam on Kerr foundation subjected to a moving oscillating load[J]. Shock and Vibration, 2018, 37(1): 14− 20.

Analysis of metro vibration load excited on the tunnel induced by moving trains

HUANG Qiang1, LIU Ganbin1, WAN Ling2, ZHU Yaohong1, HUANG Hongwei3

(1. Institute of Geotechnical Engineering, Ningbo University, Ningbo 315211, China;2. School of Engineering, Jiangxi Agricultural University, Nanchang 330045, China;3. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China)

Metro vibration load should be determined first before studying train-induced vibration. Previous analytical models rarely consider the effects of submodels of train, track, and subgrade in determining the metro vibration load. In the present study, effects of those submodels were extensively investigated using the train-track-tunnel-subgrade model. It indicates that when track irregularity is not considered, the train can be directly equivalent as point loads. Instead, when the track irregularity is considered, the metro vibration loads from different train models are similar while the wheel-rail force shows discrepancy to some extent. In such case, the metro train should better be simplified as the whole train model. Metro vibration load from fixed-track is maximum, from the ballast-track is second, and from the floating slab track is minimum. The floating slab track can effectively reduce the amplitude and frequency of metro vibration load, but as the slab length increases, the metro vibration load finally becomes constant. The subgrade models play little effect on the metro vibration load

metro vibration load; train model; track pattern; subgrade model; track irregularity

U211.4

A

1672 − 7029(2020)05 − 1209 − 10

10.19713/j.cnki.43−1423/u.T20190689

and can be simplified as Winkler model directly. By analyzing the effects of submodels in the analytical model, it may provide some guidance on the determination of the metro vibration load.

2019−08−01

国家自然科学基金重点资助项目(51538009)；宁波市自然科学基金资助项目(2019A610399)

刘干斌(1976−)，男，江西吉安人，教授，博士，从事土动力学与地下工程方向教学科研工作；E−mail：liuganbin@nbu.edu.cn

(编辑 蒋学东)