图的主独立数
章芳芳,叶淼林
(安庆师范大学数理学院,安徽安庆246133)
设图G= (V,E),|V|=n,定义在V上的一个双值函数f:V→{ - 1,1 },如果满足条件:V中至少一半的顶点v使得
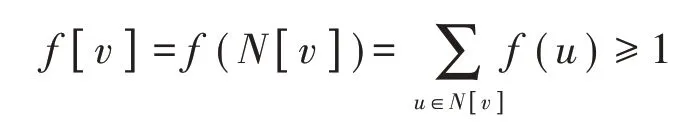
成立,这里N[v]=N(v)⋃{v},则称f为图G的一个主控制函数[1-2]。图G的主控制数[1-2]定义为

文献[3-7]给出了图的主控制数的一些结果,本文提出图的主独立数的概念:
设G=(V,E)为一个图,一个双值函数f:V→{ - 1,1 },如果满足条件V中至少一半的顶点v使得f[v]≤1 成 立 ,则 称f为 图G的 一 个 主 独 立 函 数 。 图G的 主 独 立 数 定 义 为αmaj(G)=为图G的一个主独立函数且f(V)=下面讨论主独立数的性质和下界。
定理1对于任意的n阶连通图G,均有
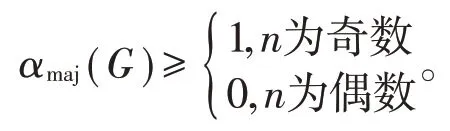
证明(1)当n=2l+1 为奇数时,将V划分成两个部分:V(G)=V1⋃V2,且V1⋂V2=φ, |V1|=l, |V2|=l+1且使 |E(V1,V2) |尽可能大(这里E(V1,V2)表示一端点在V1中,另一端点在V2中的所有边构成的集合)。定义图G的一个主独立函数f
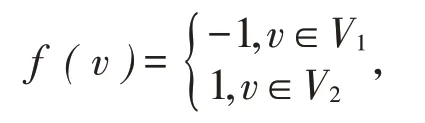
当u∈V2时,有否则将此点u移至V1中,使得新的更大,这与拆分要求中的 |E(V1,V2) |尽可能大相矛盾,故有f[u]≤1,所以f为图G的一个主独立函数,而

故αmaj(G)≥f(V)=1。
(2)当n=2l+2为偶数时,取u∈V(G)使得2l+1阶图G-u为连通图。
由(1)知,存在一个主独立函数f1,使得f1(V(G-u))=1。扩充f1到f定义f(u)=-1,则f为图G的一个主独立函数,且f(V)=f1(V(G-u))+f(u)=1+(-1)=0。故αmaj(G)≥f(V)=0,综上所述,定理1成立。
推论1若n≥2为整数时,有

证明由主独立数的定义和任意完全图各点地位相同即知。
推论2当n≥2为整数时,有αmaj(K1,n)=n-1。
证明由图K1,n的特征,分拆V(G)=V1⋃V2,其中 |V1|=1, |V2|=n。定义K1,n的主独立函数f:当v∈V1时,f(v)=-1;当v∈V2时,f(v)=1。故f为K1,n的一个主独立函数,且此时f(V)的值是最大的,故

推论3当n≥m≥ 2均为整数时,有

证明令G=(V,E)且G≅Km,n,其中n≥m≥ 2 为整数,且U和W为G的二部划分顶点集,且 |U|=m,|W|=n。令f为G上的最大主独立函数,且在f下给W中尽可能多的顶点标号为+1。令U+和U-为U的顶点集,他们的顶点在f下的标号分别为+1和 -1。W+和W-也类似定义,则
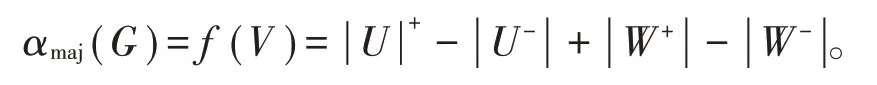
当m=n时,W中至少有一个顶点w使得f(N[w])≤ 1 成立,如果需要,可重新定义U和W;当m<n时,因为V中的顶点在f下至少一半的闭包和小于等于1,知道W中至少一个顶点w有f(N[w])≤ 1 成立。对这样一个顶点w,有f(w)+f(U)=f(N[w])≤ 1,故f(U)≤1-f(w)≤2。
现证明W=W+,即证W中每个顶点在f下均被标号为+1。假设有W-≠∅,若U=U-,则令g:V→{ - 1,1 }为一个双值函数,定义
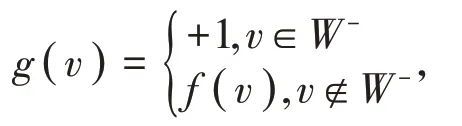
则g(N[w])=g(U)+g(w)=1-m≤ 1 对每个w∈W成立。因为n≥m,即 |W|≥ |U|,可得g是值大于f的一个主独立函数,这与f的定义矛盾,故至少存在一个顶点u在U+中。现令h是V→ { - 1.1 }的一个双值函数,定义因f(U)≤2,故h(U)=f(U)-2 ≤ 0,所以h(N[w])=h(U)+h(w)≤0+1≤1。因为n≥m,即|W|≥ |U|,可得,h是G上的一个主独立函数,h下W中标号为+1的顶点数比f在W中标号+1的顶点数多,这与f的定义矛盾,所以W=W+。现令f(N[w])≤ 1,其中w∈W,则f(U)+f(w)=f(N[w])≤1。即f(U)≤1-f(w),故|U+|-|U-|=f(U)≤1-f(w)=0,所以|U+|≤|U-|。又m=|U+|+|U-|,可得所以。进一步,对V中的个顶点在f下的标号均为-1,剩下的个顶点在f下的标号均为+1,于是可得到G上一个值为的一个主独立函数。因此有

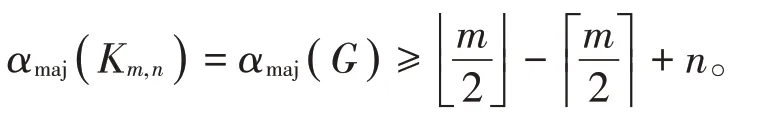
推论4对任一正整数k,则存在一个完全二部图G使得αmaj(G)≥k。
推论5对任意n阶r正则图且G(r≥ 2),均有。
证明令G是一个n个顶点的r正则图且G=(V,E),假设f是V上的一个主独立函数,且

令V-记为V中的满足f(N[v])≤ 1的顶点集,则因此有

又因为当v∈V-时,f(N[v])≤ 1;当v∈V+时,f(N[v])≤r+1,故


定理2当m≥0为整数时,令P(m,αmaj)表示主独立数为m的连通图的最小阶数,则有

证明令G=(V,E)是一连通图,且αmaj=m。现在考虑G上的一个最大的主独立函数f,又令P和M是G的顶点集,即G=P⋃M,且有
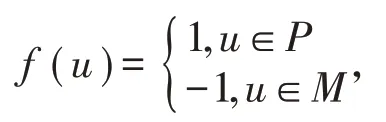
则m=f(V)= |P|-|M|。故 |M|= |P|-m,且 |P|=|M|+m,则有 |M|≥ 1,否则对G上的每个顶点v有f[N(v) ]≥2,这与f是G上的一个主独立函数矛盾,因此有 |V|= |P|+|M|=|M|+m+|M|=2 |M|+m≥m+2,并且这个下界是可以取到的,如K2,m,它是阶为m+2的连通图,且主独立数为m,综上所述有P (m,αmaj)=m+2。
定理3令为n阶图且。
证明由推论3可知下面证明。
设f是图G的一个主独立函数,且使得αmaj(G)=f(V),由主独立函数的定义知,V中至少有一个顶点v,使得注意到从而V中至少有个顶点在f下的标号为-1,即V中至多有个顶点在f下的标号为+1,故有
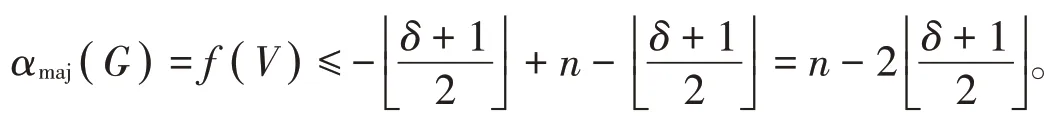
图的主独立数是图的一个新的分支,本文主要给出了图的主独立数的概念和一些相关的性质特征,但是还有新的问题需要去研究,这里就不一一阐述了。

