带小参数的半线性椭圆方程Dirichlet边值问题的可解性

石 曼，钟金标

（安庆师范大学数理学院，安徽安庆246133）

文献[1]利用上下解等方法，研究了问题

正解的存在性和唯一性，并证明了当参数充分大时，其正解不存在，这里区域Ω是洞型区域，Γ1、Γ2分别是Ω的内外边界，参数λ1＞ 0,λ2＞ 0。

文献[2]研究了问题

正解的存在性与不存在性，其中参数λ＞0，Ω是Rn中的有界光滑域，非线性函数f是次线性的。

文献[3]讨论了问题

正解的存在性。

受文献[1-3]的启发，本文利用不动点定理在实体区域上研究半线性椭圆方程边界值问题

的可解性，并且在一定条件下研究了解的唯一性与不存在性。这里Ω是ℝn中有界光滑域，参数λ＞0，非线性项f(x,u)满足的条件比文献[1-3]中的非线性项更为一般。现假设问题(1)中的函数满足或部分满足下列条件：(H1)f(x,u)＞ 0,x∈Ω且f(x,u)连续为递减的。

引理1若条件(H1)成立，则问题(1)的解为正解。

证明由(H1)知-Δu＞0,x∈Ω，又由上调和函数极值原理及知u≥ 0。

引理2当参数λ充分小时，问题

仅存在平凡解u≡0。

证明在（3）式两边乘以u，并在Ω上积分，同时利用Green第一恒等式及Poincare不等式得：

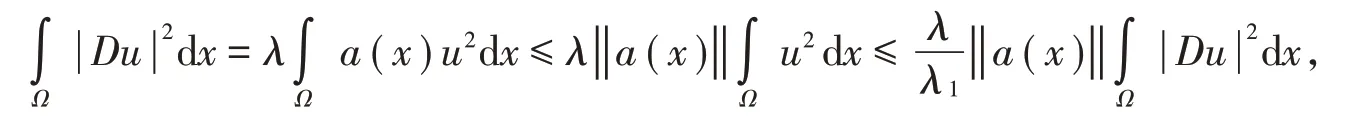
引理3（不动点定理）[4]设X是一个Banach空间，B是X的一个闭凸子集。若T是B到B的一个紧映射，R为一个正常数。使对满足的任意u∈B有u≠tT(u)，0 ≤t≤ 1，则T有一个不动点u∈B且。

下面讨论问题（1）解的存在性。

定理1设条件(H1)(H2)成立，且λ充分小时，则问题（2）也就是问题（1）至少存在一个有界正解。

证明记则K为X的一个闭凸子集。定义算子

T:K→K为由F(x,u)非负连续，L-1是紧正算子[5]，T:K→K可以断定存在一个常数R＞ 0，使对满足‖u‖=R的∀u∈K和有u≠tT(u)。

若不然，则在( 0,1 ]中存在序列tn和K中满足‖un‖→+∞(n→ +∞)的序列，有

即这个不动点为问题（1）的解。下面讨论（1）式的唯一性与不存在性。

定理2若条件（H2）成立，则问题（1）最多只有一个解。

证明设u1,u2为问题（1）的两个解，则

可得：

结合条件(H2)知u1=u2。

定理3若条件(H2)成立且当参数λ充分大时，问题（1）无有界正解。

证明记为-Δ算子在区域Ω中0-Dirichlet 边值问题的第一特征值，φ为相应的特征函数，记在方程-Δu=λf(x,u)两边乘以φ，同时在Ω上积分，并利用Green第二恒等式及条件(H2)得从而所以于是当λ充分大时，问题（1）无有界正解。

下面给出实例说明所得结果的有效性。

例考察问题的可解性，其中Ω为不包含原点的有界光滑域，这时从而满足条件(H1)；又关于s∈(0,+∞)为递减的，从而满足条件(H2)。由定理1知，当参数λ充分小时，问题至少存在一个有界正解。又由定理2知，解唯一。当参数λ充分大时，由定理3知无有界正解。

综上所述，本文利用不动点定理、算子理论、调和函数极限原理、Green第一恒等式等相关理论讨论了一类带小参数的半线性椭圆方程Dirichlet边值问题正解的存在性、唯一性以及不存在性，并给出了实例证明了相关定理的有效性。