有序Hadamard型分数阶积分微分方程解的存在性
李耀红,张海燕,2
(1.宿州学院数学与统计学院,安徽宿州234000;2.安徽大学数学学院,安徽合肥230601)
近年来,分数微分方程模型在理论和应用上广受关注,它是处理力学、控制理论、信号和图像处理等领域中数学问题精确描述的一个重要工具,相关研究有许多优秀成果[1-5]。需要指出的是,目前大多数已有研究结果都是就Riemann-Liouville或Caputo分数阶定义的微分方程,而基于Hadamard分数阶定义的微分方程问题研究相对较少。Hadamard 分数阶定义中包含以对数函数为底的幂指函数,计算复杂,但其在解决某些涉及对数运算的分数阶方程模型时十分有效[6-7]。最近,文献[8]研究了一类有序Caputo分数阶微分方程组解的存在性,文献[9]讨论了几类有序Hadamard分数阶微分方程初值问题,并利用变参数技巧获得相应问题解的存在性。
受上述文献结果的启发,本文考虑如下有序Hadamard分数阶微分方程:

这里D(⋅)和I(⋅)分别定义为 Hadamard 分数阶导数和积分是一个连续函数。和文献[8-10]相比,本文非线性项中含有Hadamard分数阶积分和导数,这和已有研究问题显著不同,而且研究结果在应用上更为方便,同时边值条件为Hadamard分数阶积分形式,其涵盖多点边值条件,适用范围更广。特别地,通过引入一些记号,简化了解存在性的研究过程。
1 预备知识
定义1[1]函数g:[1,+∞)→ℝ的α阶Hadamard分数阶积分定义为
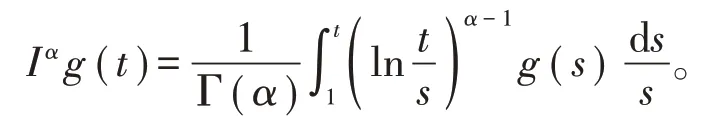
定义2[1]函数g:[1,+∞)→ℝ的α阶Hadamard分数阶导数定义为

其中n-1<α<n,n=[α]+1。
引理1[1]若α> 0,u∈C[1,e]⋂L[1,e],则IαIβu(t)=Iα+βu(t),Dα(Iαu(t))=u(t),

其中ci∈ℝ(i=1,2,…,n),n如定义2所述。
引理2若y(t)∈C([1,e],ℝ)且1<α≤2,则有序分数阶微分方程

在边值条件(2)下有唯一解
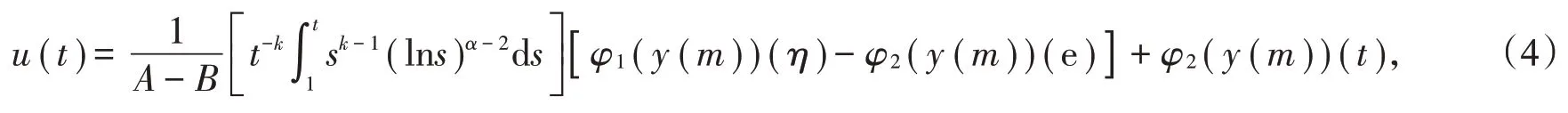
其中A≠B,且,
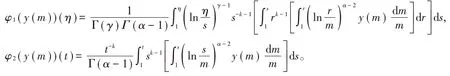
证明对(3)式两边利用积分算子Iα积分,从引理1可知方程(2)的通解为
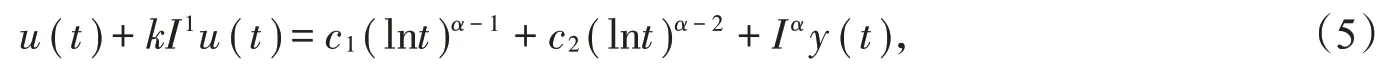
由边值条件u(1)=0,可知c2=0。接着对(5)式求导,则
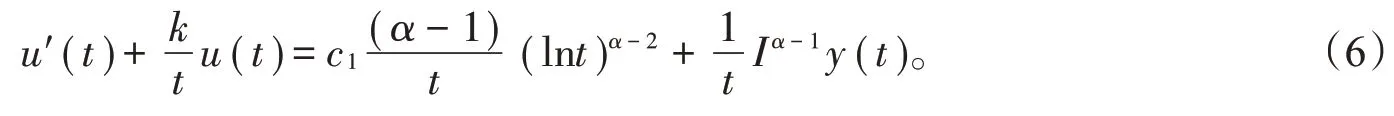
在(6)式两边乘积分因子tk,化简得

对(7)式两边同时积分知

又由边值条件u(e)=Iγu(η)知
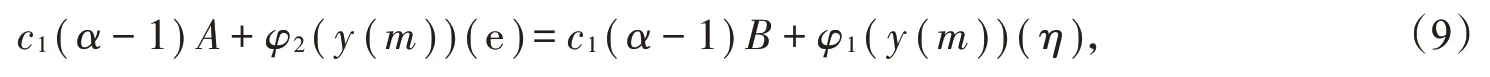
故

将c1代入(8)式即得(4)式,引理得证。
引理3(Banach压缩不动点定理)[11]设D是Banach空间X的闭子集,T:D→D是一个严格的压缩映射,即∀x,y∈D,|Tx-Ty|≤k|x-y|成立,其中0 <k< 1,则F在E中有唯一不动点。
引 理 4(Leray-Schauder 抉 择 原 理 )[11]设T:D→D是 一 个 全 连 续 算 子 ,令M={x∈D:x=λT(x),0 <λ<1 },则要么M是E中无界集,要么T在D中至少有一个不动点。
2 主要结果
记X={u|u∈ C([1,e],ℝ )且Dβu∈C([1,e],ℝ )},显然X在范数
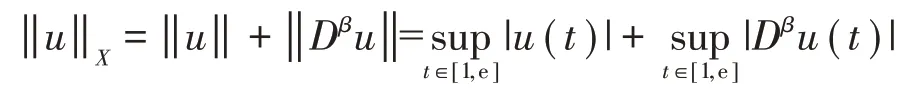
下是一Banach空间。依据引理2,定义算子T:X→X如下:
则有序Hadamard分数阶微分方程(1)和(2)有解等价于算子Tu(t)=u(t)在X中有不动点。为方便计算和表示,记:
引理5若任意y∈C[0,1],则有
证明(i)由于则
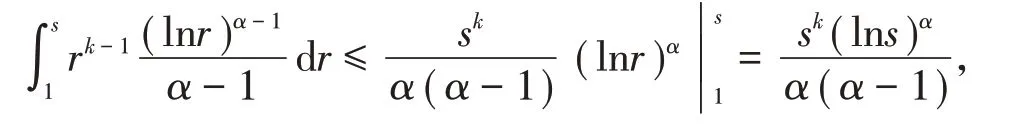
从而(i)式得证。类似计算易证(ii)和(iii)结论成立。
定理1假若g:[1,+∞)→ℝ是一个连续函数且对任意xi,yi,zi∈ℝ(i=1,2)满足下面
Lipschitz条件:
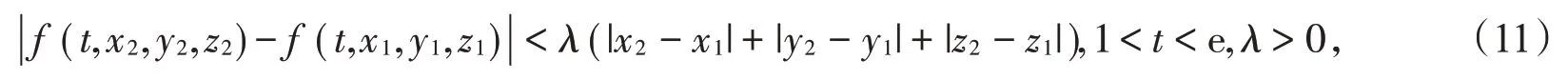
且λHF<1,则有序分数阶微分方程(1)和(2)在X中存在唯一解。
证明令定义

则TMr⊂Mr。事实上,对任意u∈Mr,根据(11)式可知
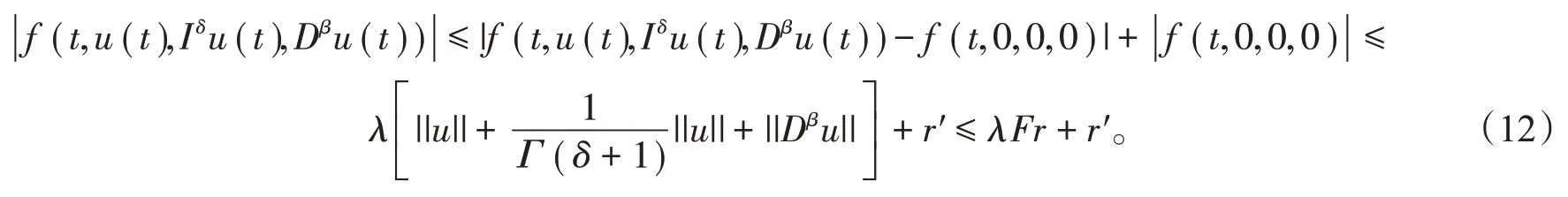
于是由引理5知|Tu(t)|≤G(λFr+r′)。
又注意到
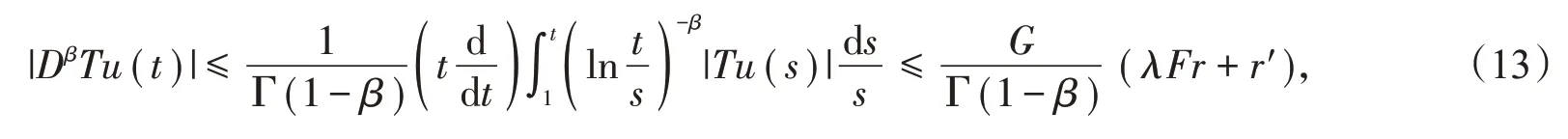

类似于(13)式有

结合(14)和(15)式有

注意到λHF<1,故T是压缩算子。从而由引理3知算子T在Mr中有唯一不动点,即有序Hadamard分数阶微分方程(1)和(2)在X中存在唯一解。
定理2假若g:[1,+∞)→ℝ是一个连续函数且存在实数μi>0(i=0,1,2,3),使得

成立且HL<1,则有序分数阶微分方程边值问题(1)和(2)在X中至少有一个解,这里
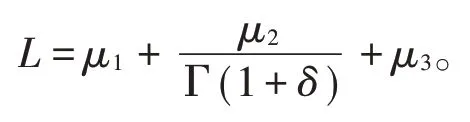
证明首先分3个步骤证明算子T在X中是全连续的。首先,根据函数f的连续性易知算子T也是连续的;接着,任取有界集其中l>Hμ0(1-HL)-1,则对∀u∈Ml,依据(16)式知


同时,当t2→t1时,有
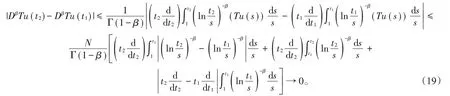
因此当t2→t1时,由(18)和(19)式有
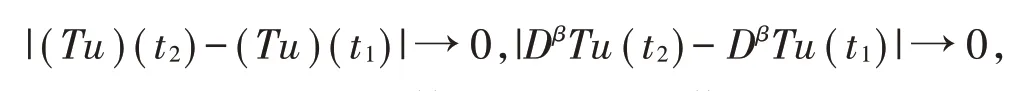
即||(Tu)(t2)-(Tu)(t1)||X→0,则T在Ml上是等度连续的。依据以上3步结果,由Arzela-Ascoi′s 定理可知算子T在Ml上是全连续的。
下面再证明算子T在X中具有不动点。记M={u(t)|u∈X,u=θ(Tu),θ∈(0,1)},故M是有界的。这是因为,对∀t∈[1,t],u∈M,由(16)式有

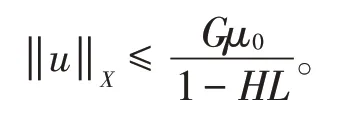
又因为HL<1,故M是有界集,于是由引理4知算子T在X中至少有一个不动点,即有序分数阶微分方程(1)和(2)在X中至少存在一个解。
例考虑如下有序Hadamard分数阶微分方程积分

这里
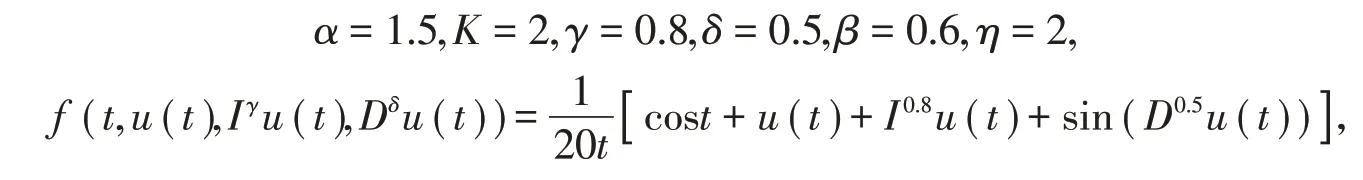
则
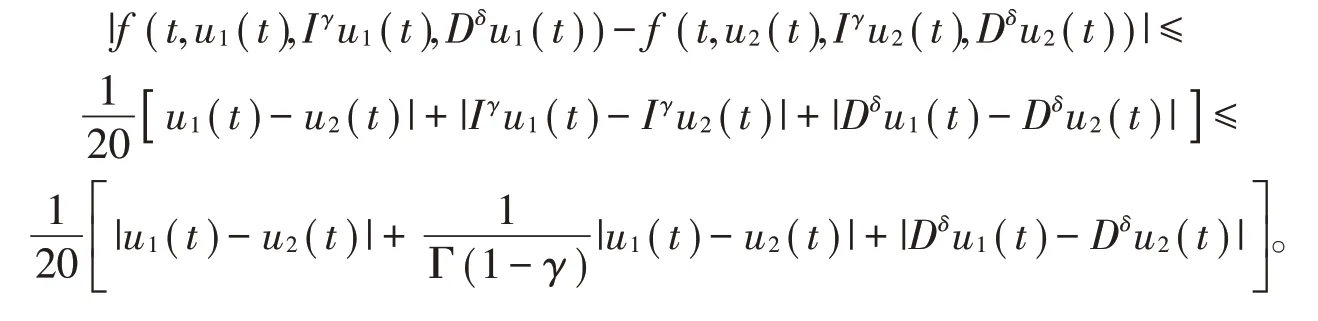
3 总 结
本文利用Banach压缩不动点定理和Leray-Schauder抉择原理,结合一些新引入的函数简记符号,研究了一类具有Hadamard积分边值条件的有序Hadamard分数阶积分微分方程边值问题,获得了该问题解存在唯一性的充分条件,并通过例子说明结果的应用。特别地,当(2)式中η=1 时,则u(1)=0,u(e)=0,问题(1)(2)为典型的分数阶微分方程两点边值问题,因此本文研究问题是两点边值问题的推广,具有更广泛的应用价值。

