数字半群的商的Frobenius数和亏格
石雅言,孙广人
(安庆师范大学数理学院,安徽安庆246133)
令ℕ 表示所有非负整数构成的集合,若ℕ 的子集S满足加法封闭,0 ∈S,且S关于ℕ 的补集为有限集,则称S是一个数字半群。设A是ℕ的一个非空子集,用A表示由A生成的( ℕ ,+ )的幺子半群,即

设n是数字半群S的一个非零元,则数字半群S关于n的Apéry 集表示为Ap(S,n)=对于任意一个数字半群,只要确定了数字半群S中任一非零元n的 Apéry 集,则S的Frobenius数和亏格即可确定。数字半群的Frobenius问题是数字半群领域中的经典问题[2-4],对于嵌入维数为2的数字半群的Frobenius数和亏格的相关问题已经得到解决。目前,对于嵌入维数大于2的数字半群的Frobenius数和亏格还没有一般的计算公式。
设S是数字半群,p为正整数,则数字半群S的商表示为数字半群的商的Frobenius 问题是由线性Diophantine Frobenius 问题变形得来,假设n1,n2,…,np,d都是正整数,且,线性Diophantine Frobenius问题是找到最大的不属于且整除d的数的计算公式,即数字半群的Frobenius 数。文献[5]中已经得出了形如的数字半群的Frobenius数和亏格的计算公式,本文研究的是形如的数字半群,通过d模3余数的不同,分成3种情况,通过确定该类数字半群的极小生成元系,进而得到Apéry集,最后得出3种情况下数字半群的商的Frobenius数和亏格的计算公式,并给出证明。
1 相关引理
引理1[1]设S是数字半群,p为正整数,则是数字半群当且仅当p∈S。
引理2[1]设a和b都是正整数,且gcd(a,b)=1,则
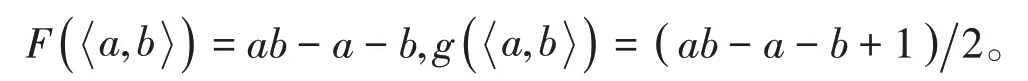
引理3[1]设S是数字半群,n是S中非零元,则Ap(S,n)={ 0 =w( 0 ),w( 1 ),…,w(n-1 )},其中w(i)是S中与i模n同余的最小的数,其中i∈{ 0 ,1,…,n-1 }。
引理4[1]设S是数字半群,n是S中非零元,则
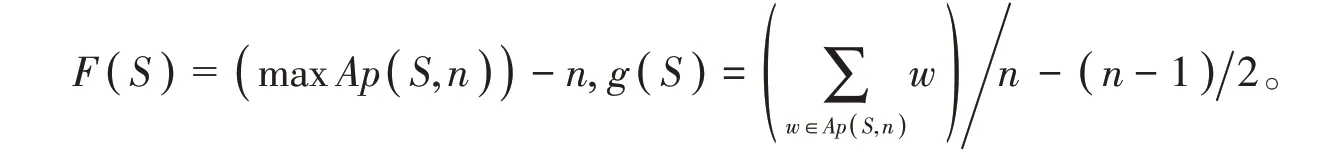
2 主要结论
对于数字半群a,a+k,a+3k d,根据d模3 余数为0、1、2 得到3 种情况,下面给出3 种情况下数字半群a,a+k,a+3k d的Frobenius数和亏格的计算公式并证明。
定理1设数字半群S=a,a+k,a+3k,其中a,k为正整数,gcd(a,k)=1,a=sd,且d=3t,t为正整数,则F(S d)=s2t+ (k-t-1)s-k,g(S d)=[s2t+ (k-t-1)s-k+1 ]2。
证明由引理1 知是数字半群。由gcd(a,k)=1,知gcd(d,k)=1,任何属于S的元素都可表示成ax+ (a+k)y+ (a+3k)z的形式,其中x,y,z为非负整数。要使属于S的元素能被d整除,即d|ax+ (a+k)y+ (a+3k)z,所有形如[(a+k)y+ (a+3k)z]d的整数都满足d|y+3z,其中y,z∈{ 0 ,1,…,d-1 }。 数 对 (y,z)满 足d|y+3z,其 中y,z∈{ 0 ,1,…,d-1 }的 所 有 数 对 为(d-3,1 ),(d-6,2 ),…,( 0,t),…,(3 ,3t-1 ),[(a+k)y+ (a+3k)z]d的对应值为3st+k-2s,3st+k-4s,…,st+k,…,3st+3k+2s,显然s∈S d,st+k∈S d,可得数字半群S d中每一个元素都可由集合{s,3st+k-2s,3st+k-4s,…,st+k,…,3st+3k+2s}线性组合生成,而{s,3st+k-2s,3st+k-4s,…,st+k,…,3st+3k+2s}中每一个元素都可由集合{s,st+k}线性表示,故因此S d=由gcd(s,k)=1知gcd(s,st+k)=1,再由引理2可得:

定理2设数字半群S=a,a+k,a+3k,其中a,k为正整数,gcd(a,k)=1,a=sd,且d=3t+1,t为正整数,则,
当s-1=3p时;
当s-1=3p+1时;
当s-1=3p+2时。
证明由引理1 知是数字半群。由gcd(a,k)=1,知gcd(d,k)=1,任何属于S的元素都可表示成ax+ (a+k)y+ (a+3k)z的形式,其中x,y,z为非负整数。要使属于S的元素能被d整除,即d|ax+ (a+k)y+ (a+3k)z,所有形如[(a+k)y+ (a+3k)z]d的整数都满足d|y+3z,其中y,z∈{ 0 ,1,…,d-1 }。数对(y,z)满足d|y+3z,其中y,z∈ { 0 ,1,…,d-1 }的所有数对为
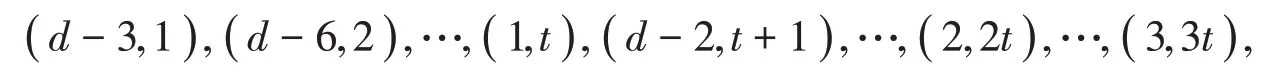
[(a+k)y+ (a+3k)z]d的对应值为
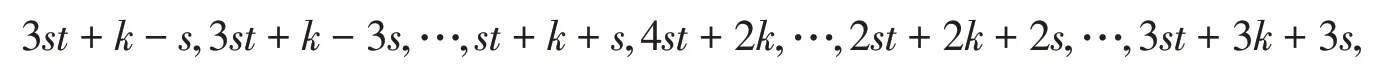
显然s∈S d,st+k+s∈S d,a+3k=3st+3k+s∈S d,可得数字半群S d中每个元素都由集合{ }s,3st+k-s,3st+k-3s,…,st+k+s,4st+2k,…,2st+2k+2s,…,3st+3k+3s线性组合生成。而集合{ }s,3st+k-s,3st+k-3s,…,st+k+s,4st+2k,…,2st+2k+2s,…,3st+3k+3s中每一个元素都可由集合{ }s,st+k+s,3st+3k+s线性表示,故因此S d=故由引理3知,

当s-1=3p时 ,,
当s-1=3p+1 时 ,,
当s-1=3p+2 时。
定理3设数字半群其中a,k为正整数,gcd( )a,k=1,a=sd,且d=3t+2,t为正整数,则,
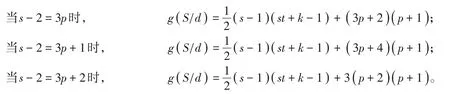
证明由引理1 知是数字半群。由gcd(a,k)=1,知gcd(d,k)=1,任何属于S的元素都可表示成ax+ (a+k)y+ (a+3k)z的形式,其中x,y,z为非负整数。要使属于S的元素能被d整除,即d|ax+ (a+k)y+ (a+3k)z,所有形如[(a+k)y+ (a+3k)z]d的整数都满足d|y+3z,其中y,z∈{ 0 ,1,…,d-1 }。数对(y,z)满足d|y+3z,其中y,z∈ { 0 ,1,…,d-1 }的所有数对为[(a+k)y+ (a+3k)z]d的对应值为
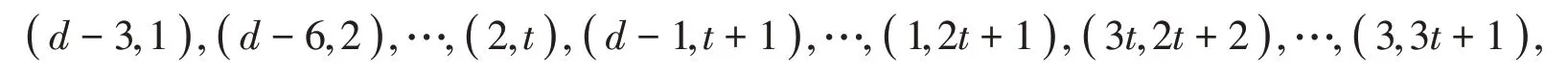
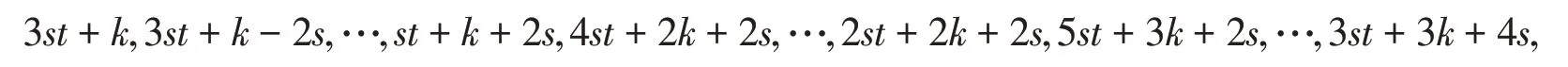
显 然s∈S d,st+2s+k∈S d,2st+2s+2k∈S d,a+3k=3st+2s+3k∈S d,可 得数字半群S d中每一个元素都可由集合
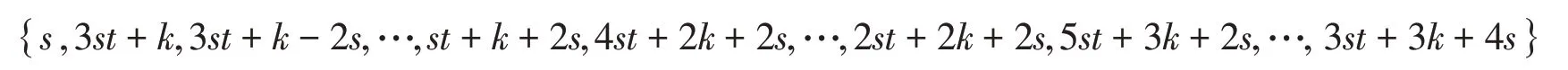
线 性 组 合 生 成 。 而 集 合 {s,3st+k,3st+k-2s,…,st+k+2s,4st+2k+2s,…,2st+2k+2s,5st+3k+2s,…, 3st+3k+4s}中每一个元素都可由集合{s,st+2s+k,2st+2s+2k,3st+2s+3k}线性表示,故因此故由引理3知,

则由引理4可得,
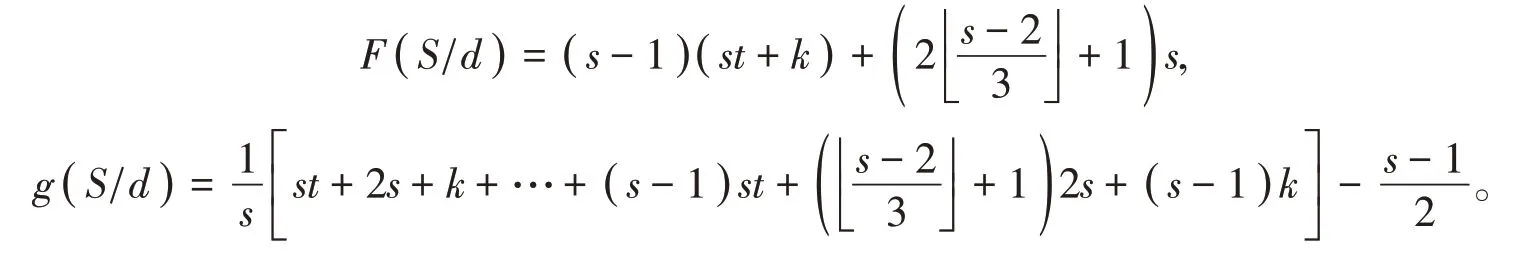
当s-2=3p时,
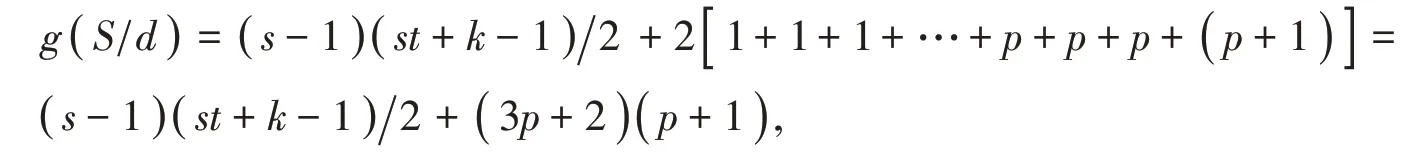
当s-2=3p+1时,

当s-2=3p+2时,

