基于规划航迹的“三自”光纤惯导系统航向耦合效应抑制技术
唐江河,詹双豪,尉 超,何长久,曲雪云,简凯宁
(1.北京自动化控制设备研究所,北京 100074;2.火箭军装备部驻北京地区第六军事代表室)
0 引言
“三自”光学惯导系统具有高精度及便于维护的特性,近年来在国内发展迅速。由于激光陀螺自身特性的优势,“三自”激光惯导系统的旋转调制技术在国内外已发展较为成熟[1-3]。而光纤陀螺具有可靠性高、无机抖装置(利于旋转机构控制)、随机游走误差相对较小等优势[4-6],利于“三自”光纤惯导系统实现快速高精度启动,可以满足武器系统快速反应能力的要求[7]。这一优势在弹用领域已得到发挥,而在长航时导航方面,“三自”光纤惯导系统仍是国内研究的重要方向。
相对于激光陀螺,光纤陀螺安装误差、安装不正交度以及标度因数等参数稳定性限制了“三自”光纤惯导系统长航时导航精度的提升。其主要原因是载体运动航向的不确定性导致系统外环翻转时由陀螺标度因数和安装误差等诱发的水平失调角不断累积,产生航向耦合效应,严重影响了参数自补偿效果。针对单轴旋转惯导系统,文献[8-10]中指出可通过航向隔离解决航向耦合效应问题,然而针对“三自”光纤惯导系统仍没有文献进行相关技术的研究。本文将从双轴旋转惯导系统的旋转方案入手,在分析航向耦合效应机理的基础上,证明“三自”光纤惯导系统航向耦合效应的不可解耦性;并针对无人飞行器、无人潜艇以及导弹等要求规划航迹的载体,提出了一种基于规划航迹的旋转方案自适应调整技术,以有效抑制航向耦合效应,提升系统长航时导航精度。
1 双轴旋转方案介绍
光学陀螺具有对g不敏感、无运动部件、动态范围宽以及标度因数线性度好的特点,使旋转调制技术在捷联惯导领域得到极大发展。而旋转方案设计是旋转调制实现的基础,一直是国内外学者的重要研究方向,尤其双轴旋转方案的研究更是其研究重点[11]。
MK49系统采用3个Honeywell公司生产的GG-1342型单轴机械抖动激光陀螺,基于双轴转动方案,定期使惯性敏感装置绕方位轴和横摇轴旋转,用来消除陀螺漂移和其他误差源。系统自主导航精度可达0.39n mile/30h,但具体的旋转方案未在任何文献上有所提及。MK49型双轴旋转式激光陀螺惯导系统已经被选为北约组织船用惯性导航的标准系统,大量装备于很多国家的水面舰体和潜艇。
图1所示为经典的双轴八位置旋转方案,该方案很好地调制了安装误差和标度因数误差,但对陀螺标度因数不对称性没有补偿效果。为此,文献[12]改进了该旋转方案,得到如图2所示十六位置旋转方案。该旋转方案在失调角层面不仅调制了陀螺和加速度计的零偏、标度因数以及安装误差,同时对陀螺标度因数不对称性也具有很好的调制效果。同时,文中进一步提出了在十六位置方案的每一步旋转的中点(即90°或270°)增加1个位置,实现三十二位置旋转方案。该三十二位置旋转方案和十六位置旋转方案的调制效果是一样的,只是它能更好地压制旋转惯导系统的锯齿波幅值。
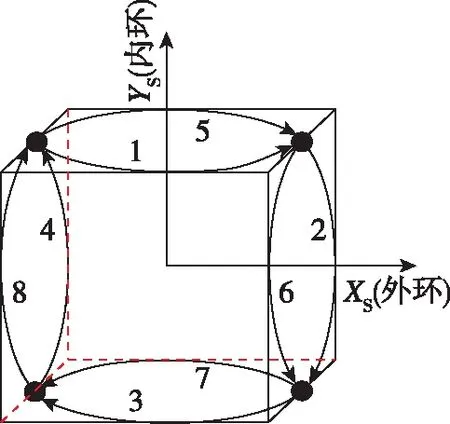
图1 八位置双轴旋转方案示意图Fig.1 Eight-sequence dual-axis rotary schematic diagram

图2 十六位置双轴旋转方案示意图Fig.2 Sixteen-sequence dual-axis rotary schematic diagram
这两种旋转方案虽然在系统失调角层面具有很好的调制效果,但在速度层面的调制效果有限,尤其是陀螺安装误差会引起系统速度误差的增长。为此,文献[1]对十六位置旋转方案进行了改进,有效地提高了系统速度层面的调制效果,其旋转方案示意图如图3所示。

图3 改进十六位置双轴旋转方案示意图Fig.3 Improved sixteen-sequence dual-axis rotary schematic diagram
国内外对载体机动与旋转调制的交联耦合作用也进行了分析。文献[8-10,13]针对单轴旋转调制惯导系统开展了航向耦合效应分析,并提出了通过载体航向机动隔离,即系统旋转机构在执行预先设计的旋转方案的同时反向叠加载体的航向机动,可以有效地抑制载体航向机动对旋转调制的影响。文献[14]针对双轴旋转方案进行了航向耦合效应分析,但只是针对某一特定的旋转方案进行了机动条件下的误差分析,并没有从理论机理上开展研究。
本文将从理论分析入手开展航向耦合效应机理研究,并以改进十六位置旋转方案为例,针对要求规划航迹的载体提出了一种航向耦合效应的有效抑制方法。不同于现阶段弹上“三自”惯导机械锁定导航方式,文中提出的方法要求“三自”惯导系统工作于旋转导航方式。为了保证飞控系统或其他设备满足惯导系统姿态输出精度要求,不仅要求“三自”惯导系统利用旋转框架角度进行姿态解调,而且还要精确标定补偿旋转轴系安装误差。
2 坐标系定义
涉及的坐标系定义如下:
惯性坐标系(i):原点与地球质心重合,Xi轴沿地球转轴指向地球北极,Yi轴和Zi轴在赤道平面内,不随地球旋转,且Zi轴和初始时刻当地东向重合。
地理坐标系(g):定义为北天东坐标系。
台体坐标系(p):利用3个加速度计的敏感轴方向OXa、OYa、OZa进行定义,X加速度计的敏感轴方向OXa即为Xp、Yp在OXaYa所在平面内,且与OXa垂直;Zp与Xp、Yp满足右手定律。
惯导坐标系(b):当惯导的2个环架都锁定为0时,台体坐标系即为惯导坐标系,为便于分析,文中定义的初始惯导坐标系与地理坐标系一致。
3 航向耦合效应机理分析
3.1 “三自”光纤惯导系统导航误差模型
为便于分析,选用惯性导航坐标系,利用形式相对简单的Ψ方程进行分析。
(1)
式中

其中:ε0为陀螺漂移误差;δkg为陀螺标度因数误差;mg为陀螺安装误差;ng为陀螺安装的不正交度。
那么经简化后系统的姿态和速度误差的解为

(2)
有

式中:L为当地纬度;ωie为地速数值;γ、ρ和φ分别为基座坐标系相对于地理坐标系的滚动、俯仰和航向;α和β分别为旋转机构外环和内环的旋转角度;ω1和ω2分别为外环和内环的旋转角速率。
(3)

(4)

(5)

3.2 航向耦合效应对导航误差影响分析
双轴旋转方案中内环旋转子流程只需利用内环轴进行载体航向机动隔离即可解耦航向耦合效应;但对于外环翻转子流程,“三自”光纤惯导系统没有天向旋转自由度进行航向机动的隔离,航向耦合效应的解耦将非常复杂,而其中陀螺标度因数误差、陀螺安装误差及安装不正交度与系统航向之间的解耦是航向耦合效应分析的关键。为便于分析,只考虑载体航向机动,且外环翻转过程中航向保持不变。以下将针对双轴旋转方案中外环翻转子流程,分别证明三类误差源航向耦合效应是否具有可解耦性。
证明3个误差参数航向耦合效应是否具有可解耦性,即是要证明是否存在一种外环翻转方式,使相邻2次外环翻转(不妨设2次翻转外环为0°→180°→0°)诱发的姿态失调角与航向的变化无关。不妨设第1次翻转时系统航向角为φ1,第2次航向角为φ2。结合航向姿态隔离的要求[15],第1次t0~t1时刻翻转内外环角度由(0°,φ1)变化为(180°,-φ1),第2次t3~t4时刻由(180°,-φ2)变化为(0°,φ2)。
3.2.1 陀螺安装误差可解耦性分析
2次翻转由陀螺安装误差诱发的失调角为
上式表明,只要满足航向隔离规则,不管外环翻转流程怎么设计,陀螺安装误差的航向耦合效应都具有可解耦性。
3.2.2 陀螺安装不正交度误差可解耦性分析
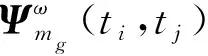
2次翻转由陀螺安装不正交度误差诱发的失调角为
构造首次外环翻转(外环0°→180°→0°)子流程:
1)用时T1旋转内环,内外环(ψ1,0°)→(0°,0°);
2)用时T2内外协调旋转,(0°,0°)→(0°,180°);
3)用时T1同向旋转内环,(0°,180°)→(-ψ1,180°)。
假定Ti时间后,相邻的第2次外环翻转子流程:
4)用时T1旋转内环,(-ψ2,180°)→(0,180°);
5)用时T2内外环协调旋转,(0°,180°)→(0°,0°);
6)用时T1同向旋转内环,(0°,0°)→(ψ2,0°)。
可以证明步骤1)、3)以及4)、6)诱发的失调角和都为0,关键需要进行步骤2)、4)的流程设计。可以证明当满足以下条件时,步骤2)、4)产生的失调角相互抵消:
(1)步骤2)或步骤4)内外环角度各自应满足:
• 内外环交错旋转,外环旋转速率恒定;
•α(t)+α(Ts+T2-t)=180,t∈(Ts,Ts+T2);
•β(t)=β(Ts+T2-t),t∈(Ts,Ts+T2);

其中,Ts为步骤2)或步骤4)的开始时刻。
(2)步骤2)和步骤4)内外环角度之间应满足
β(t)=-β(Ts2+T2-t),t∈(Ts1,Ts1+T2)
其中,Ts1和Ts2分别为步骤2)和步骤4)的开始时刻。
3.2.3 陀螺标度因数误差可解耦性分析
2次翻转由陀螺标度因数误差诱发的失调角为
若要求陀螺标度因数具有可解耦性,则有
那么
=0
必然要求:φ1=±φ2或φ1±φ2=π。
这与航向机动的任意性矛盾,因此陀螺标度因数误差具有不可解耦性。
4 基于规划航迹的旋转方案自适应调整
由3.2节的分析可知,将外环翻转子流程调整为3.2.2节所描述的流程后,通过相邻2次翻转可以实现:
1)陀螺安装误差和不正交度诱发失调角为0;
2)产生的失调角来自于标度因数误差,可证明

(6)
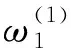
4.1 常规导航旋转方案的限制
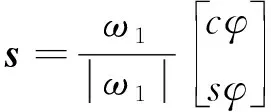


图4 外环旋转矢量合成示意图Fig.4 Schematic diagram of outer gimbal rotation vector synthesis
4.2 基于规划航迹的旋转方案自适应调整方法
当具备规划航迹的前瞻载体航向信息时,有以下定理。外环翻转合矢量将被压制在一个有界区间内,导航误差得到有效抑制。

l1=s′2i-1+s′2i,l2=s′2i-1-s′2i,l3=-l1,l4=-l2

该定理即是要证明可以从4个矢量中选择1个矢量,假定为l,满足
(7)


图5 定理证明示意图Fig.5 Schematic diagram of theorem proving
1)当30°≤θ≤90°时,取l=-l2,可满足式(7)。

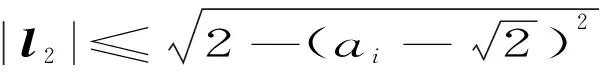
由此可以递推得到序列{ai},且有
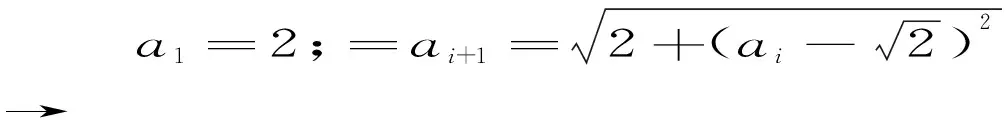

由递推的思想,该定理得证。
根据该定理,可以设计调整方案:每2次外环旋转进行1次调整,由以往外环旋转矢量在水平面上投影的矢量和调整相邻2次外环旋转方向,使得以往的矢量和与该次旋转矢量以及下一次旋转矢量的矢量和的模达到最小。
4.3 仿真验证


图6 旋转方案自适应调整后水平失调角曲线Fig.6 Horizontal misalignment angle curve after adaptive adjustment of rotation scheme
5 试验验证
为了进一步验证旋转方案自适应调整策略的有效性,利用一套“三自”光纤惯导系统进行了转台验证试验。试验主要对比了旋转方案一(按照图3所示的改进十六位置旋转方案)和旋转方案二(4.3节介绍的旋转方案)的导航精度。
试验时,“三自”光纤惯导系统水平固定于转台上,准备时间和准备流程都一致,时间为10min,完成了初始对准以及一些主要误差参数的标定。为了能有效激励航向耦合效应,同时能准确获得下一次外环旋转时的航向角度,惯导系统完成对准后,转台以恒定的0.5(°)/s绕天向轴匀速旋转(下一次外环旋转时的航向角度由恒定旋转速率计算获得),导航时间为8h。为充分验证,方案一和方案二分别进行了2次试验。4次试验的导航径向误差曲线如图7所示,虚线所示为方案一的2次试验位置误差曲线,实线所示为方案二的2次试验位置误差曲线。图7中显示,方案二最大位置误差不超过800m,而方案一最大位置误差都超过了6200m。表1对4次试验位置误差的TRMS值进行了处理。表1中,试验1和试验2为方案一对应的2次验证试验,试验3和试验4为方案二对应的2次验证试验。由表1可知,方案二的TRMS均值为0.34nmil,而方案一的TRMS均值为2.02nmil,精度提升了83.2%。

图7 位置误差对比曲线Fig.7 Comparison curve of position error
表1 位置误差的TRMS值
Tab.1 TRMS value of position error

试验TRMS/nmileTRMS均值/nmile精度提升/%12.2121.8330.3240.362.020.3483.2
6 结论
本文从理论上证明了“三自”惯导系统航向耦合效应的不可解耦性,但针对通过规划航迹能获知前瞻航向信息的特殊应用场合,提出了一种旋转方案自适应调整策略:首先采用分段构造外环旋转策略解耦陀螺安装误差和安装不正交度与航向的耦合关系,将航向耦合效应的误差源都归结到陀螺标度因数误差;然后基于外环旋转矢量和最小原则进行外环旋转方向的自适应调整,达到抑制陀螺标度因数误差的目的,文中还对该自适应调整策略的抑制效果给出了严格证明。
文中提出的旋转方案自适应调整策略取得了良好效果。试验证明,10min准备时间,导航8h,位置精度(时间真均方根误差(Time Real Root Mean Square Error,TRMS))达到0.34nmile,相对改进十六位置旋转方案提升了80%以上。

