新型磁悬浮振动陀螺的设计与分析研究

曾 凯，吴宇列，肖定邦

(国防科技大学智能科学学院，长沙 410073)

0 引言

振动陀螺是一种利用哥氏效应对角运动进行测量的传感器，它没有传统陀螺的机械转子摩擦问题，相比光学陀螺体积更小。随着微机电系统(Micro-Electro-Mechanical System，MEMS)制造技术的发展，振动陀螺以其体积小、成本低、可靠性高等优点，在精确制导弹药、汽车和消费电子领域得到广泛应用[1-2]。目前，较典型的振动陀螺包括半球谐振陀螺(Hemispherical Resonator Gyro，HRG)、四质量块式速率积分陀螺(Quadruple Mass Gyro, QMG)、盘形陀螺(Disc Resonator Gyro，DRG)等[3-5]。然而，这些振动陀螺的性能均受到很多因素的影响。振动陀螺实现高精度的基础必须有一个高稳定的主振动，目前影响振动稳定性最主要的因素是谐振子的结构误差和结构阻尼，使得驱动振动方向与实际振动方向不一致，引起检测模态的漂移，进而降低陀螺的灵敏度和零偏稳定性[6]。所以,振动陀螺性能的提升仍是该领域内的热点研究方向之一。

目前所有报道的振动陀螺中，其谐振子都是通过支撑锚点与基座连接在一起的。而锚点的实际制造工艺很难保证其结构和材料的均匀性，所以常常会影响谐振子的结构精度和阻尼均匀性[7]。在机械转子陀螺领域，转子轴承的磨损是限制陀螺性能提升的重要影响因素。为解决该问题，利用气浮、液浮、磁浮、静电悬浮等方式将转子悬浮起来，从而极大地减小了摩擦以达到提高转子陀螺精度和寿命的目的[8-9]。其中,通过电磁悬浮方法来减少摩擦的研究比较集中，主要包括电磁悬浮陀螺、静电悬浮陀螺、反磁悬浮陀螺和超导磁悬浮陀螺四大类[10]。

这些悬浮式的转子陀螺之所以能够实现较高的精度，是因为采用悬浮技术将转子悬浮起来，其悬浮系统是关键。将敏感元件悬浮起来，避免了其与基座的直接接触而减少摩擦，且便于实现多自由度运动驱动，扩大了应用范围[11-12]。在电磁悬浮结构设计中，主要包括上拉吸引式和下推排斥式两种结构。吸引式磁悬浮结构的悬浮体位于电磁线圈的下部，利用电磁感应产生的磁吸力与悬浮体的重力平衡，达到悬浮的效果[13]。这种悬浮方式的系统参数方便调节，但是只有竖直方向的力，抗冲击能力差；当水平方向出现扰动时，只能依靠很弱的边缘效应进行控制，难以实现平衡。排斥式磁悬浮结构的电磁线圈和永磁体位于悬浮物的下部，在电磁线圈和永磁体的共同作用下给悬浮物提供排斥力与其重力平衡实现悬浮[14]。排斥式磁悬浮结构的斥力主要由永磁体提供，可以降低装置的功耗及发热。另外，由于它同时受到电磁线圈和周围永磁体的力，所以具有较强的抗干扰能力。

根据振动陀螺的原理，结合排斥式悬浮结构的特点，本文提出了一种全新结构的磁悬浮振动陀螺。该陀螺利用磁悬浮技术将谐振子悬浮起来实现角速度测试，降低了对谐振子和锚点的制造精度要求，在陀螺性能的提升方面具有很大的潜力。文章的第一部分介绍了振动陀螺的基本工作原理，并推导了驱动模态和检测模态固有频率差值对陀螺性能的影响规律；第二部分详细介绍了所提出的新型磁悬浮振动陀螺的结构及其振动模态，并利用仿真软件对其磁场分布进行了研究以说明其均匀性；在第三部分进行了实验测试，陀螺样机的测试结果验证了该新型陀螺测量角速度的能力；最后,对本文进行了总结及展望。

1 磁悬浮振动陀螺理论分析

图1 磁悬浮振动陀螺的示意图Fig.1 Sketch map of the electromagnetic suspended vibratory gyroscope

磁悬浮振动陀螺的示意图如图1所示，它的谐振子是图中的悬浮质量块。首先通过控制磁场分布使得质量块稳定悬浮，即谐振子的重力G与磁力Fz相等；然后改变磁场分布，在谐振子的横向添加一个激励磁力fx，使得谐振子在x方向振动。定义质量块在x方向的振动模态为驱动模态(Drive mode)，而在y方向的振动模态为检测模态(Sense mode)。当系统有角速度Ω输入时，谐振子一方面相对系统有x方向的平动，另一方面随着系统相对惯性坐标转动,所以它会在y方向产生哥氏加速度，等效为激励出y方向振动即检测模态的哥氏力。由于哥氏力与输入的角速度是成比例的，所以通过检测y方向的振动信号即可解算出输入的角速度Ω。

该磁悬浮振动陀螺中，由于采用磁悬浮技术将谐振子悬浮后再实现振动激振，谐振子无锚点的限制将会降低陀螺的频率误差和机械结构阻尼，大大提升陀螺的性能。另外，由于振动元件独立于陀螺结构，可近似成集中质量块，其谐振频率只取决于可测量和控制的悬浮力与电阻尼，而与其结构精度无关，从而降低了谐振子制造误差带来的影响。此外，可以通过闭环控制悬浮谐振子的振动运动轨迹，保证驱动方向与实际振动方向一致，从而保持了振动的稳定性，减小检测模态的零偏漂移。

图2 磁悬浮振动陀螺的动力学模型Fig.2 Kinetic model of the electromagnetic suspended vibratory gyroscope

基于上述动力学模型，可以得到质量块在x和y方向的运动方程为

(1)

可知y方向的稳态解为

y=y0sin(ωt+φy)

(2)

y0为y方向振动的幅值，表示为

(3)

其中，x方向的振动幅值x0为

(4)

ωx和ωy分别是x和y方向的固有频率，Qx和Qy则分别是2个方向上的品质因数。在实验中为了获得最大的响应幅值以方便检测，激励力fx的频率被设置为与驱动模态(x方向)的固有频率相等，即ω=ωx。

假设y方向的品质因数为10，检测模态的响应幅值随着ωx/ωy的变化规律如图3所示。可以发现，当2个模态固有频率的比值为1时(即频率裂解值为0)，振动的响应幅值达到最大，对应的灵敏度最高。磁悬浮振动陀螺由于磁场均匀性比较好，并且谐振子可视为集中质量块，所以2个模态的振动频率基本一致，频率裂解值比较小。另外，由于磁悬浮谐振子控制的复杂性，其振动频率通常较低，为实现高灵敏度，应尽可能提高振动频率，使其接近和或达到谐振频率。

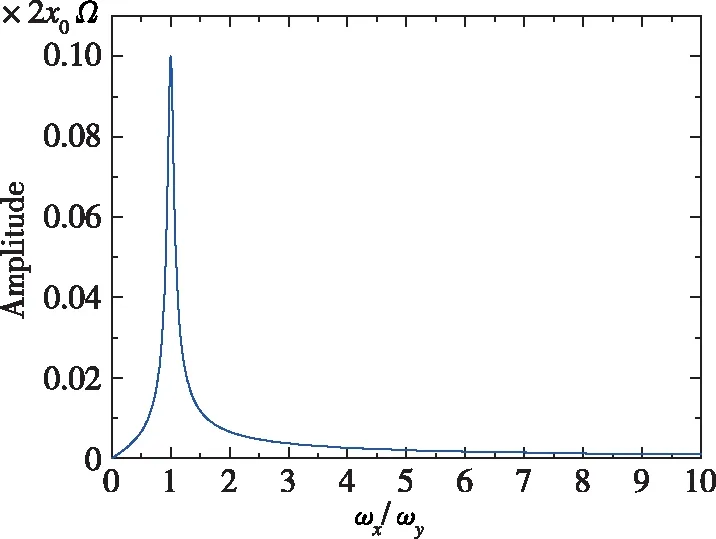
图3 检测模态的响应曲线Fig.3 Response curve of sense mode

2 磁悬浮振动陀螺结构设计及其磁场分布

2.1 结构设计

图4所示为所设计的新型磁悬浮振动陀螺的结构示意图及其实物图，它主要由上部分的悬浮质量块(Suspended mass)和提供磁悬浮力的下部磁悬浮平台组成。上部分的质量块是一个由多片磁性材料组成的圆柱体，通过改变磁性材料的数量及尺寸可以改变振动质量，它被悬浮在平台的正上方。下部分的磁悬浮平台主要由外围的永磁体(Perma-nent magnet)、中间的绕组线圈(Winding coil)和内部的霍尔元件(Hall sensors)组成。磁性悬浮质量块正是受到永磁体和绕组线圈共同产生的磁力而实现稳定悬浮和振动的，其中外围的8个永磁体对质量块产生均匀的吸引力，而中间的4个绕组线圈则为悬浮质量块提供浮力，浮力的大小可以通过改变输入线圈的电流来实现调节。内部的3个霍尔元件用来检测悬浮质量块在x、y和z方向上的位置，进而为绕组线圈提供反馈信号来实现质量块的稳定悬浮。通过上述方式，实现了悬浮质量的悬浮，消除了支撑锚点会带来的缺陷，从而提高了质量块在各个方向上参数的均匀性。

(a)原理图

(b)实物图图4 新型磁悬浮振动陀螺结构Fig.4 The novel electromagnetic suspended gyroscope structure

2.2 模态分析

由于该悬浮质量块在此结构中可看作刚体，即视为集中质量点，所以主要考虑它的平动。如图5所示，该结构的振动模态主要为质量块在水平方向(x、y)和竖直方向(z)的运动[15]。该结构的振动质量即为悬浮质量块的质量(样机的悬浮质量为500g)，而刚度及阻尼主要取决于电磁场的分布。

(a)水平方向

(b)竖直方向图5 模态分析Fig.5 Mode analysis

依据陀螺的工作原理可知，谐振子的振动方向应与角速度的输入方向垂直才能产生明显的哥氏效应。因此，为测量该结构的轴线方向角速度输入，应采用谐振子在水平方向的振动模态，对该方向的振动进行激励及检测。

当质量块稳定悬浮于平台上时，在绕组线圈中加入相应的激励电压，使得质量块在驱动模态(x方向)稳定振动。当平台绕其中心对称轴转动时，由于哥氏效应会在检测模态(y方向)上激励出振动。此时平台内部的霍尔元件将会检测出悬浮质量块的振动信号，将检测模态方向的振动信号提取出来即实现了其信号检测。由于检测模态的振动信号与输入角速度是成比例的，所以通过解调检测模态的振动信号，即可得到输入角速度的大小。

2.3 磁场分布

在上述陀螺中，当质量块振动时主要受到磁场力的影响，进而影响陀螺的性能。为了研究质量块振动时其附近的磁场变化，利用有限元软件ANSYS对其进行了仿真研究。因为该陀螺是对称结构，所以将其结构简化为如图6所示的二维模型。模型的上部是一个悬浮质量块，两侧是提供吸引力的永磁体。由于悬浮质量块也是由磁性材料组成的，所以它和永磁体的N极在图6中都是朝上的，且两者磁性材料的矫顽力均为182975A/m(2300Gs)。在模型的中间有2个绕组线圈，线圈的中心为铁芯，两侧为线圈截面。绕组线圈的匝数为650，输入的电流约为1A。因为绕组线圈给质量块提供排斥力，而质量块的N极朝上，所以通入的电流应使线圈的N极朝下。模型中除了绕组线圈铁芯的相对导磁率为1000外，其余材料的相对导磁率都为1。利用上述参数对磁悬浮振动陀螺的磁场进行计算，得到如图6所示的磁场分布及磁感线。可以发现，磁感应强度最大的位置在绕组线圈铁芯的顶部，这是因为绕组线圈、永磁体和质量块产生的磁场都汇集于此。

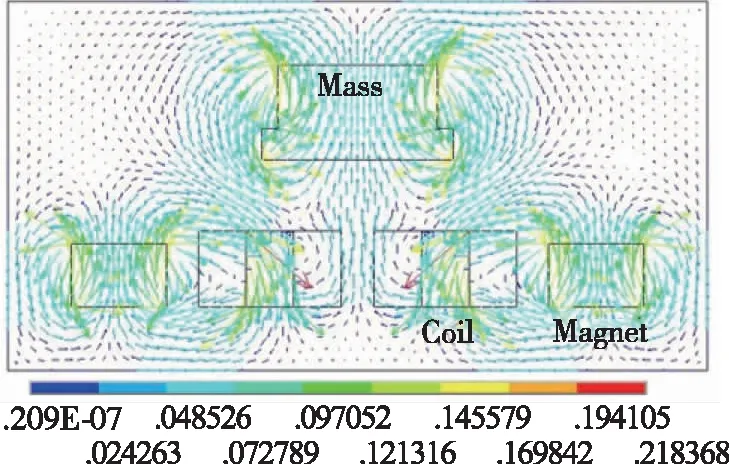
图6 磁场分布图Fig.6 Distribution of magnetic field

在悬浮质量块的实际振动中，它的振动幅值约为0.5mm。为了研究其振动过程中的磁场变化，分别计算了悬浮质量块在振动时的极限位置和初始位置处的磁感应强度。图7所示为当质量块位于初始位置和极限位置时的磁感应强度云图，从图7中可以看出悬浮平台中每个位置区域的磁感应强度大小。通过比较悬浮质量块位于不同振动位置处的磁感应强度云图可以发现，磁场分布基本是一致的，最大磁感应强度的变化也很小。磁感应强度的最大值从0.2184T增加到0.2218T，变化量为3.4mT，只改变了1.6%。此外，由于所设计的磁悬浮陀螺是对称的，所以在不同方向的磁感应强度云图都一样。对于悬浮质量块而言，它在空中主要受到电磁力的影响，所以磁感应强度的均匀性是其刚度和阻尼均匀性的首要前提。

(a)初始位置

(b)极限位置图7 磁感应强度云图Fig.7 Cloud chart of magnetic flux density

3 陀螺样机测试

为了进一步确认其测试角速度的能力，对陀螺样机进行了实验测试。图8所示为实验测试装置，将磁悬浮振动陀螺安装于转台(Turntable)上且随着转台转动，其驱动和检测模态的振动信号由悬浮平台中的霍尔元件进行测试，并将测试信号连接至示波器(Oscilloscope)便于观测和保存。当悬浮质量块稳定地在驱动模态振动时转动转台，哥氏力在检测模态激励出的振动信号将会由该方向的霍尔元件进行输出。

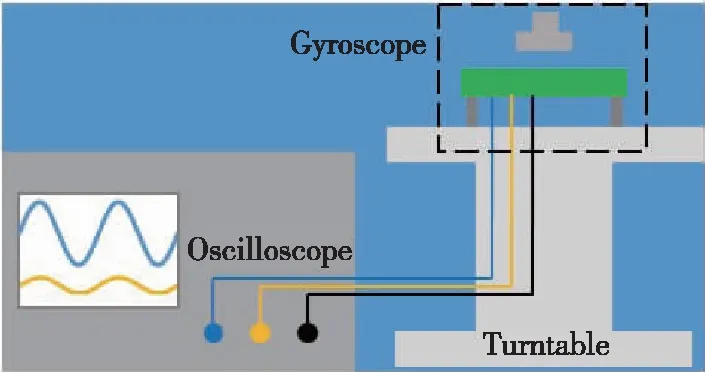
(a)原理图

(b)实物图图8 测试装置Fig.8 Testing device

利用x和y方向的霍尔元件将悬浮质量驱动模态和检测模态的位移信号实时输出，并对其信号做傅里叶变换得到的频谱图如图9所示。图9(a)是驱动模态的测试信号，可以发现它的振动信号表现出较好的周期变化规律。由于该陀螺样机的固有频率为20Hz，所以激励信号的变化频率设置为与此相等，因此在频谱图中可以在20Hz处发现一个明显的峰值。当转台转动时，由于哥氏效应检测模态也会输出振动信号，其测试信号和频谱图如图9(b)所示。不难看出，检测模态的实时信号也呈现出明显的周期变化规律，且频谱图中最大的峰值亦出现在20Hz处。这说明哥氏力能够在检测模态方向上激励出同频的振动信号，检测模态振动的幅值约为驱动模态的10%左右。通过测试陀螺的标度因子，即可由检测模态的振动幅值得到输入的角速度。

(a)驱动模态

(b)检测模态图9 振动信号及傅里叶变换频谱图Fig.9 Vibration signals and spectrum

为了获得该陀螺样机的标度因子以进一步说明检测模态对角速度的响应，测试了陀螺在转台不同角速度输入下检测模态的输出。通过改变转动平台的转动速度，分别记录了检测模态在0(°)/s,1(°)/s,5(°)/s,10(°)/s, 15(°)/s,20(°)/s下的实时振动信号，并对其做了傅里叶变换。图10所示为测试结果，纵坐标为每种角速度下测试信号傅里叶变换的峰值。总体来看，随着输入角速度的增加，检测模态输出的信号也逐渐增强。经过线性拟合得到测试陀螺的标度因子为1.6mV/ [(°)/s]，其线性拟合的相关系数R2=0.81。在该磁悬浮振动陀螺中，影响其标度因子稳定性的因素主要是磁悬浮电路的稳定性。

图10 检测模态在不同角速度下的输出信号Fig.10 Output signal of sense mode at different angular speeds

4 结论

本文针对一般振动陀螺中普遍存在的结构误差和结构阻尼的问题，提出了一种新型的磁悬浮振动陀螺，以减小陀螺的漂移，提升陀螺性能。相关分析及实验结果表明：

1)所提出的磁悬浮振动陀螺谐振子无支撑锚点，消除了现有振动陀螺中因锚点带来的阻尼和结构误差的影响，为振动陀螺性能的提升提供了新思路。

2)磁悬浮振动陀螺的灵敏度与振动频率有关，应尽可能提高振动频率，使其接近谐振频率。

3)所设计的陀螺样机实现了角速度的测量，具有明显的陀螺效应。目前，陀螺的噪声和稳定性还有待进一步提高。由于影响噪声和稳定性的主要因素一个是悬浮电路板，另一个是谐振子的谐振频率相对较低，接近外界环境干扰频率。下一步应该优化悬浮电路，并提高谐振频率达到千赫兹，以减小外界干扰的影响，提升陀螺性能。