基于二分法的EKF-SLAM算法

闫旭亮，杨功流，王 璐

(北京航空航天大学仪器科学与光电工程学院，北京 100083)

0 引言

随着机器人技术的不断发展和相关技术的突破，机器人逐渐被应用在军事侦察、海底探索、核污染测定、扫雷排险等环境恶劣且极其危险的情况下[1-2]。机器人技术被认为是21世纪的核心武器，将成为新的工业技术革新的核心，由于机器人技术的前景充满了无数种未知的可能性，世界各国对它的研究越来越重视[3]。

在众多考量机器人的指标中，机器人的移动能力是决定其任务成败的关键，机器人自由移动的能力是建立在其对周围环境特征的了解层次基础上的[4-5]。只有当移动载体机器人深入了解周围的环境特征时，才可以更快更准确地完成任务，因此迫切需要一种能够精确定位并且创建环境地图的方法，同步定位与地图创建(Simultaneous Localiza-tion and Mapping，SLAM)技术应运而生[6-7]。SLAM，是指机器人移动平台在行进时创建环境地图，同时根据创建的地图进行定位，利用2个信息的相互关系不断地修正来改善推算得到的数据结果。同鸡和蛋的问题类似，定位和地图创建之间相互联系，精度互为相关。

在SLAM中，常用的表示地图的典型方法有三种，分别是特征地图、栅格地图和拓扑地图。其中，特征地图不需要对地图的全局进行描述，而是只需要对有环境特征存在的地方进行描述即可，这样做可大大减少地图的计算量，提高定位的精度[8-9]。对于占用空间较小的物体可以通过计算物理中心，用点的坐标进行表述；对于由线段或由线段组合组成的特征，可以利用每个线段的描述来对特征进行表述[10-13]。本文从线特征的角度出发，提出了一种基于二分法的线特征模拟观测器，并通过MATLAB软件对其正确性和在扩展卡尔曼滤波(Extended Kalman Filter，EKF) SLAM中的适用性进行了仿真验证。

1 基于EKF的SLAM算法

SLAM的同时定位和构建地图的过程可以用估计—观测—更新的简化模型来描述。SLAM的实现流程图如图1所示，机器人移动平台从某一位置出发，按照一定的路径在未知环境中行进。每一时刻，机器人移动平台利用分析传感器采集到的信息得到的结果，同步计算出机器人移动平台的位置和周围环境地图的特征信息，完成定位和对地图更新的任务。理论上，SLAM的状态信息误差和初始误差及观测误差相关。图1中，xk为机器人移动平台在k时刻的状态，Zk为k时刻机器人移动平台的观测值，mj为环境地图中的特征信息，uk为机器人移动平台在k时刻的控制输入信号。

图1 SLAM实现流程图Fig.1 Flow chart of SLAM implementation

基于EKF的SLAM算法状态矩阵包含机器人移动平台的位姿以及环境中的路标特征

(1)

其中，机器人移动平台的位姿为

(2)

环境路标特征为

(3)

若为点特征，则用其在世界坐标系的坐标表示；若为线特征，则用机器人到线段的直线距离以及观测线段的起始角和终止角来表示。本文在讨论时着重于线特征的描述。

基于EKF的SLAM算法框架如图2所示。

图2 SLAM算法框架图Fig.2 SLAM algorithm framework diagram

状态协方差矩阵表述了状态信息矩阵中各个变量之间的联系[14]。在协方差矩阵中，主对角元素描述了对应状态的协方差，体现了对状态变量估计结果可能的变化动态范围；其余元素描述了不同状态变量之间的协方差，体现了两者之间的联系。正是由于各个变量之间存在的这种联系，才可以通过对重复信息的不断观测对之前得到的结果进行修正，减小误差。

1.1 机器人运动模型

在SLAM问题中，机器人载体的运动模型被认为是一个递归的过程，下一时刻的状态信息可以由上一时刻的状态信息来预测[15]。机器人的运动模型描述的是机器人的状态信息的动态变化规律，是指存在干扰噪声w和控制信号uk的情况下随时间的变化规律。常用离散化后的模型为

xk=f(xk-1,uk)+w

(4)

其中，函数f(·)为系统的状态转移函数，大部分情况下是线性的；xk表示的是k时刻系统的状态信息；uk表示的是控制信号输入；w是干扰噪声，包括轮子打滑和参数漂移等。

对机器人移动平台进行建模，简化后的模型只考虑横轴、纵轴坐标以及机器人移动平台的航向角这3个状态量，同时将各个通道的噪声假设为高斯白噪声。机器人移动平台简化后的运动模型为

(5)

其中，Vk是机器人移动平台的行进速度；ak是机器人移动平台的前轮转角；T是机器人移动平台传感器的采样处理周期；L是机器人移动平台的2个轮轴之间的距离；vx、vy、vΦ是各个通道的噪声,用于描述环境噪声等对模型精确度的影响。

其中，状态转移函数对状态信息矩阵和控制信号的雅可比矩阵为

(6)

(7)

1.2 观测模型

利用航位推算的机器人定位算法往往会随着时间的变化而不断积累单调上升，利用传感器对周围环境进行感知来对估计算法进行校正可提高定位的精度[16]。由于激光传感器探测精度高、抗干扰能力强以及测量范围广泛，本文采用激光传感器作为观测手段。

激光传感器的输出值是障碍物和激光仪之间的距离以及和激光仪始发处的角度，即极径和极角。

Z=[rθ]T

(8)

其中，Z是观测器的输出信号。

观测器的量测模型表述了机器人位姿和环境中障碍物两者之间的相对关系。量测方程如下

Zk=h(Xk)+wk

(9)

其中，Zk是k时刻激光仪的输出信号；h(·)是量测函数；wk是量测噪声，表述环境噪声和模型的精确度的影响。

在本文的SLAM问题中，量测模型可写为

(10)

其中，(xi,yi)描述的是在探测到的特征中的第i个特征在世界坐标系中的位置。

量测模型相对于状态矩阵的雅可比矩阵为

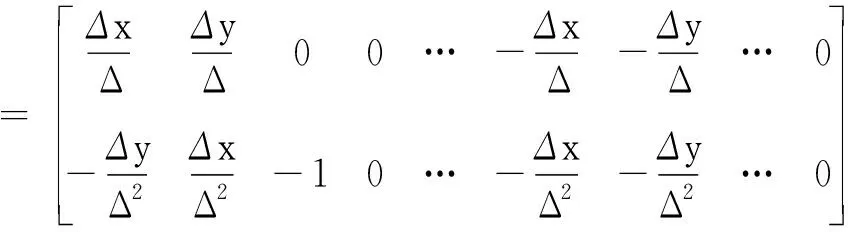
(11)

其中

(12)

1.3 数据关联

路标在世界地图中的位置可用坐标原点在直线上的投影点的坐标来表示，称为路标特征点。在k时刻，机器人观测到路标时首先需要判断观测到的路标是否已经记录在状态矩阵中。常用的判断方法是计算观测路标的特征点和状态矩阵中的特征点之间的欧氏距离，当小于设定的阈值时，认为两者是同一路标，否则是新的路标。

但是，欧氏距离在数据分析中有2个缺陷。第一，当两点固定时，欧式距离并不是固定不变的，当选用不同量纲时得到的结果也会不同；第二，当2个变量之间存在某种联系时，欧氏距离并不能体现出这种联系。因此，本文引入数据之间的协方差阵进行计算，公式如下

D2(x,y)=(x-y)TV-1(x-y)

(13)

其中，x和y表示状态矩阵中的特征点坐标和观测路标的特征点坐标，V表示观测引起的方差。

当计算距离大于阈值时，判断为新的路标，将观测路标的特征点加入状态矩阵中扩充状态矩阵；当距离小于阈值时，判断为已经存在的路标。此时，观测到的路标特征点为观测信息，因为路标为静态，所以特征点保持不变，即转移矩阵为单位阵，利用EKF方程进行状态矩阵更新。

2 线特征模拟观测器构建

在基于点特征的SLAM仿真时，可以通过判断点到机器人的距离和夹角是否满足设定的要求来判断点特征是否被观测到，然后通过人为地加上随机噪声来模拟实际的观测过程。在线段特征的模拟观测时，可以把线段特征拆分为点特征，按照点特征模拟观测的方法进行模拟观测。但是，线段特征是由无数个点的特征组合到一起的。若把一个线段拆分为几十甚至上百个点，那么一条线段特征的计算量将变的很大，更不用说几个、十几个线段特征组成的模拟环境。

二分法是一种通过不断利用排除法，将不可能的解集排除在外，通过不断排除减小函数的解区间来得到满足误差条件的解的近似值的算法，而对于线段特征的模拟观测过程可以理解为函数求零点的过程。设路标上的点到机器人的直线距离为d，观测器的模拟观测最大距离为Dmax，假设存在以下函数F=d-Dmax。那么，函数的零点的含义是模拟观测器可观测点所到的范围的临界值，当d继续增加时，路标上的点到机器人位置之间的距离将大于模拟观测器的最大观测距离，线段特征上的点将不会再被观测到。因此，对于满足函数条件F<0的线段特征上的点将被观测到。SLAM中判断线段特征能被观测到的范围的问题，转化为了求解函数F>0的解集的问题。线特征模拟观测器构建过程可根据垂足的位置分别进行构建。其中，G表示载体机器人，AB表示线特征，O表示垂足。

如图3所示，垂足在线段以外。AB上的点到G点的距离从点A到点B单调递增。若点A到G点的距离大于Dmax，那么线段将不能被观测到；若点A到G点的距离小于Dmax，且点B到G点的距离也小于Dmax，则线段特征将能被全部观测到；若点A到G点的距离小于Dmax，点B到G点的距离大于Dmax，那么将会满足二分法中对函数f(a)·f(b)<0的要求，可以应用二分法求解临界点，点A到临界点的线段特征将能被观测到。此处以垂足在左侧为例，垂足在右侧同理。

图3 模拟观测器(一)Fig.3 Analog observer (I)

如图4所示，垂足在线段以内。此时，OB段长于OA段，则只需判断OB段即可。若OG距离大于Dmax，那么该线段特征将不能被观测到；若OG距离小于Dmax，且BG距离也小于Dmax，那么线段特征将能被全部观测到；若OG距离小于Dmax，BG距离大于Dmax，那么可以利用二分法得到OB段上的临界点，并求得关于O点的对称点，若对称点在A点左侧，则A点到临界点的线段特征能被观测到，否则对称点到临界点的线段特征能被观测到。此处以垂足在左侧为例，垂足在右侧同理。

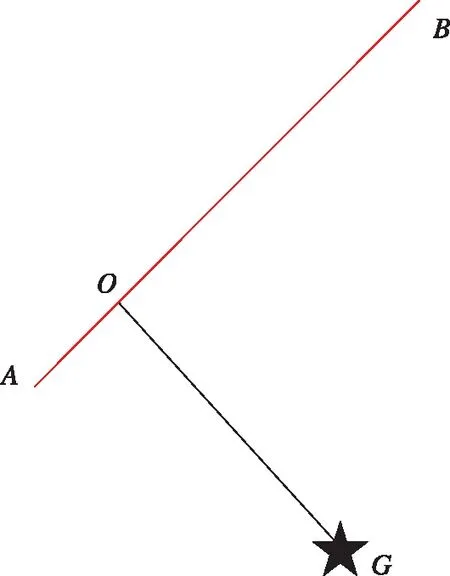
图4 模拟观测器(二)Fig.4 Analog observer (II)

在SLAM仿真时，机器人运动过程中传感器采集到的速度信息通过机器人的运动模型和设置好的运动轨迹加上白噪声进行模拟。进行地图构建时，每一时刻利用模拟采集到的速度信息和机器人运动模型由上一时刻信息推测出机器人当前时刻的位置，利用本文构建的模拟观测器可以得到观测信息，通过数据关联过程完成地图的更新和扩充，最后达到地图构建的目的。

3 仿真验证

仿真算法流程如图5所示。基于二分法的仿真实验需要设置的内容包括机器人参数、路标参数和轨迹设定参数。机器人参数设置为，速度V=3m/s，速度误差0.3m/s，车轮最大转速(π/9)rad/s,最大转向角30°，转向角误差3°，采样周期0.025s，激光雷达探测半径30m，探测距离误差0.1m，角度误差1°。路标参数设置分别为线段的左端横坐标、右端横坐标、斜率和截距。图6中的红色线段为路标，编号为1～4。参数为1(-30，0，2/3，30)，2(0,20，-1，20)，3(0,60，7/9，-35)，4(-60,0，-0.7，-35)。机器人的轨迹设定为起点(0,35)，然后分别向(25,0)、(0，-20)、(-35，0)、(-35,10)和(0,35)5个点运动，转向参数见机器人参数设置。仿真后的结果如图6所示，中间构成回路的红色线段为机器人真实轨迹，蓝色线段表示SLAM算法得到的轨迹和线特征。图7所示为轨迹估计的误差图。

图5 仿真算法流程图Fig.5 Flow chart of simulation algorithm

图6 模拟观测器仿真结果(一)Fig.6 Simulation results of analog observer (I)

图7 模拟观测器仿真误差(一)Fig.7 Simulation error of analog observer (I)

当线特征与机器人之间的距离大于雷达探测范围时被称为超限。加大3号线特征的长度，使线段左右侧端点的横坐标由45增加到60，如图8中红色虚线圈所示。超限仿真结果如图8所示，图9所示为超限仿真的误差分析图。

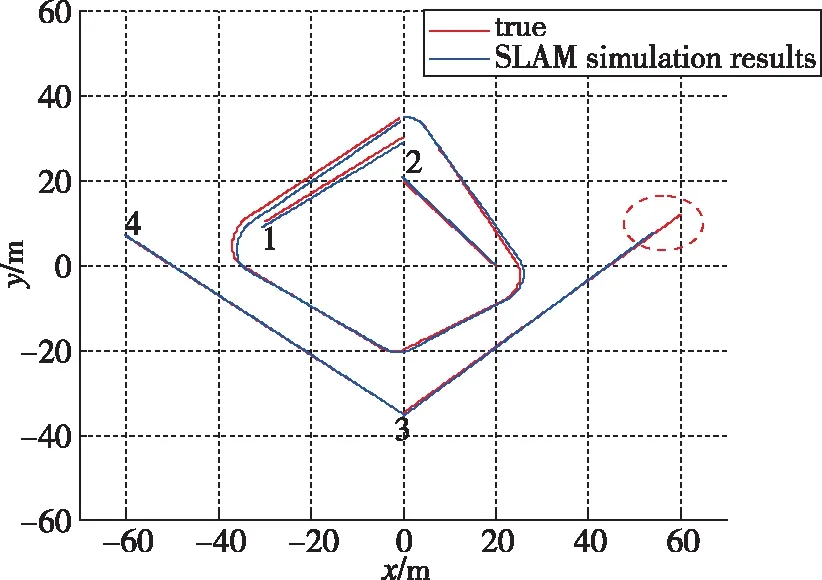
图8 模拟观测器仿真结果(二)Fig.8 Simulation results of analog observer (II)

图9 模拟观测器仿真误差(二)Fig.9 Simulation error of analog observer (II)

未出现超限时，如图6所示，模拟观测器可以观测出整条线段完成SLAM仿真；出现超限时，由仿真结果图8可以看出，观测器观测结果(蓝线)较图6的结果最右侧坐标延长至54.4412，但并未达到60，即未完全观测到延长后的线段。由于图6对应的线段较短，线段整体都在观测器可观测范围内，所以在图8中当线段延长后，观测器观测到的线段右端点横坐标延长至54.4412；但是由于线段较长，存在不可被观测到的范围，所以观测器观测到的线段右端点横坐标未达到60，这符合预期的实验结果。

上述两种情况下的仿真结果表明，基于线特征模拟观测器的SLAM仿真实验，即使出现超限情况，仍然可以得到较为准确的结果，除去未在观测范围内的部分线特征外，其余环境路标特征估计和机器人定位仍然可行。实验结果验证了基于二分法构建的线特征模拟观测器的正确性。

基于二分法和逐点法的仿真运行时间如表1所示，前三行是超限时的运行时间统计，后三行是正常时的运行时间统计。从表1中可以看出，基于二分法的仿真算法缩短了计算时间，提高了运行速度。

表1 算法运行时间对比

4 结论

本文针对线特征模拟观测时数据量过大的问题，提出了一种模拟观测器的构建方法。算法分析和仿真实验结果表明：

1)将观测器对路标的观测问题转换为函数零点求解问题。本文提出的线特征观测器利用二分法近似求解得到线特征的被观测范围，为SLAM问题中对观测问题的研究提供了新的思路。

2)相比于点特征观测器的判断过程，基于二分法的线特征模拟观测器可大量减小运算量。在满足误差条件的前提下，具有较好的实时性。

3)本文提出的线特征模拟观测器的运算量随着误差的减小而逐渐增加，在高精度的场合会影响算法的实时性，因此需要进一步改进。针对高精度的要求，需要其他方法的辅助来进一步降低运算复杂度以达到实时性的目的。