干涉型光纤传感器相位解调技术研究

李 鹏，柏 楠，陆 星

(北京自动化控制设备研究所, 北京 100074)

0 引言

光纤传感器具有灵敏度高、抗电磁干扰、耐腐蚀和体积小等优点[1]，随着光学技术及光纤器件的发展和成熟，光纤传感器在工程上逐渐得到了广泛应用。干涉型光纤传感器因其高灵敏度的显著优势，被自然灾害预测、能源勘探、水声探测等多个领域高度关注[2]。相位生成载波(Phase Generated Ca-rrier，PGC)调制解调技术作为干涉型光纤传感器信号解调的一项重要技术[3-4]，通过对光信号进行调制，使低频待测信息加载到高频调制的光信号上，然后通过解调模块，恢复出待测信息，具有灵敏度高、低频噪声较低等优点，能够很好地解决随机相位衰落等问题。PGC解调算法主要分为微分交叉相乘(Differential-and-Cross-Multiplying，DCM)算法和反正切(Arctangent, ATAN)算法。ATAN算法涉及相对复杂的反正切非线性运算，且需考虑解相位缠绕的问题；而DCM算法则采用相对简捷的微分运算，且无相位缠绕的问题，具有较高的解调效率，但是在工程应用中，存在易受光强波动和伴生调幅影响等问题。中国科学院、哈尔滨工程大学和吉林大学等科研机构针对此类问题开展了相关研究[5-8]，主要采用优化测量方案和改进解调算法等方式来提高解调性能，但在一定程度上增加了测量和算法的复杂程度[9-11]。

为消除光强波动对解调结果的影响，提高算法的解调性能，本文在传统DCM算法的基础上，提出了一种新型的改进型DCM算法，并开展了仿真和实验研究。

1 PGC解调原理

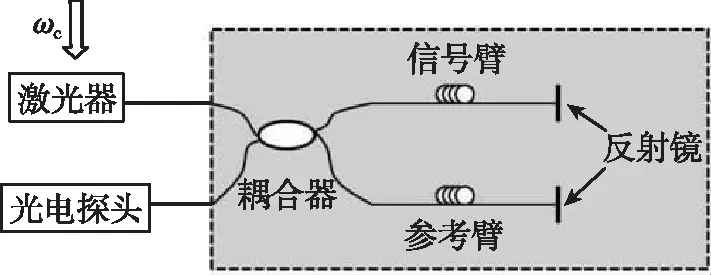
相位生成载波调制技术分为内调制和外调制两种，内调制是通过周期电信号调制激光器的光频,如图1(a)所示；外调制是通过外加周期信号改变相位差，一般将光纤缠绕在压电陶瓷(Piezoelec-tric，PZT)上，通过压电陶瓷的压电效应拉伸光纤，从而产生载波相位,如图1(b)所示。

(a)内调制

(b)外调制图1 PGC调制技术原理图 Fig.1 PGC modulation technology

外调制技术需要在光路中引入额外的调制器件如PZT，增加了系统的复杂性；内调制技术利用电信号直接对激光器进行调制，有利于实现系统的全光化。因此，以下的研究都是基于内调制技术进行的。

1.1 PGC解调的数学模型

光源输出经过内调制的激光，激光在干涉型光纤传感器中的信号臂接受外界信号的调制后，与参考臂中的激光信号发生干涉，由光电探测器将光信号转化为电信号进行采集处理。

干涉型光纤传感器输出干涉信号的光强表达式为

I=A+Bcosφ=A+Bcos(Ccosωct+θ)

=A+B[cos(Ccosωct)·cosθ-

sin(Ccosωct)·sinθ]

(1)

式中：A、B为与光强有关的物理量；Ccosωct为载波生成项，其中，ωc为载波频率，C为相位调制深度；θ=φs+φa+φ0，其中，φs为待测信号项，φs=Dcosωst，φa为其他因素引起的低频噪声项，φ0为干涉仪的初相差项。

将式(1)利用贝塞尔公式展开可得

cos(2n+1)ωct]sinθ}

(2)

将干涉信号与一倍载波信号Gcosωct混频后，通过低通滤波器滤除含有一倍载波及以上的高频部分，可以得到

I1LP=-BGJ1(C)sinθ

(3)

将干涉信号与二倍载波信号Hcos2ωct混频后，通过低通滤波器滤除含有二倍载波及以上的高频部分，可以得到

I2LP=-BHJ2(C)cosθ

(4)

1.2 DCM算法

微分交叉相乘算法流程图如图2所示。将低通滤波处理后的信号进行微分、交叉相乘、差分、积分和高通滤波等环节的处理，可以解调出所需的待测信号，具体原理如下。

图2 DCM算法流程图Fig.2 DCM algorithm process

将式(3)和式(4)进行微分运算，可得

(5)

(6)

将式(3)和式(6)、式(4)和式(5)进行相乘运算，可得

(7)

(8)

式(8)减式(7)可得

(9)

将式(9)进行积分运算，可得

I=B2GHJ1(C)J2(C)θ

(10)

将式(10)进行高通滤波，可得

φs=B2GHJ1(C)J2(C)Dcosωst

(11)

为选取合适的调制深度C值，当J1(C)J2(C)的值达到最大时，解调结果的输出信号幅度达到最大。由图3可以看出，选取J1(C)J2(C)的第1个极值点，J1(C)J2(C)的值最大，此时C值取为2.37。

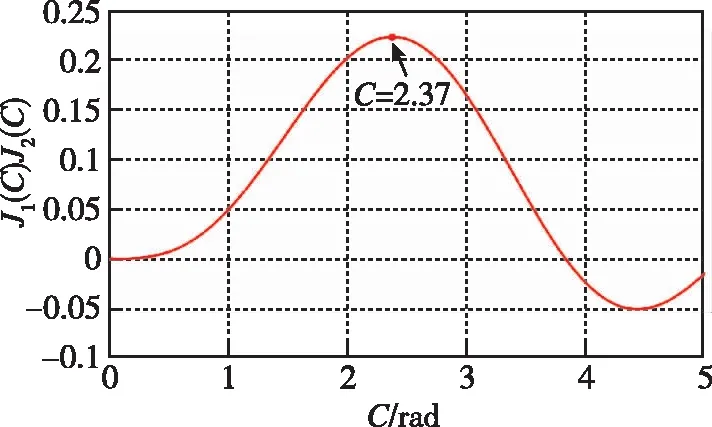
图3 J1(C)J2(C)图像Fig.3 Graph of J1(C)J2(C)

2 改进型DCM算法

传统的DCM算法的解调结果(式(11))中，含有与光强有关的B项。光强受到干扰时，直接对解调结果产生影响。改进型DCM算法将低通滤波处理后的信号进行平方相加运算，再与相减后的结果做除法运算，可以将解调结果中的B项抵消，从理论上消除光强对解调结果的影响。具体流程如图4所示。

图4 改进的DCM算法流程图Fig.4 Improved DCM algorithm process

将式(3)和式(4)进行平方运算，可得

I1LP2=B2G2J12(C)sin2θ

(12)

I2LP2=B2H2J22(C)cos2θ

(13)

式(12)和式(13)相加可得

I2LP2+I1LP2=B2(H2J22(C)cos2θ+

G2J12(C)sin2θ)

(14)

式(9)除以式(14)，可得

(15)

式(15)中，令G=H，J1(C)=J2(C)，此时，C值取为2.63，可得

(16)

将式(16)进行积分运算和高通滤波处理，可得

φs=Dcosωst

(17)

对比传统DCM算法的解调结果(式(11))可以看出，改进型DCM算法的解调结果中不含有与光强有关的B项，说明改进型的DCM算法理论上可以消除光强变化对解调结果的影响。

3 仿真研究

在MATLAB中进行仿真，研究光强波动的情况下解调算法的性能。设采样频率为500kHz，采样点数为50k；载波信号频率为50kHz，待测信号(如图5所示)的频率为200Hz，幅度为1rad。根据迈克尔逊干涉仪的特性，式(1)中，A=B，并在其中分别引入低频干扰信号(如图6所示)和随机干扰信号(如图7所示)研究光强波动对解调结果的影响。

图5 待测信号Fig.5 Target signal

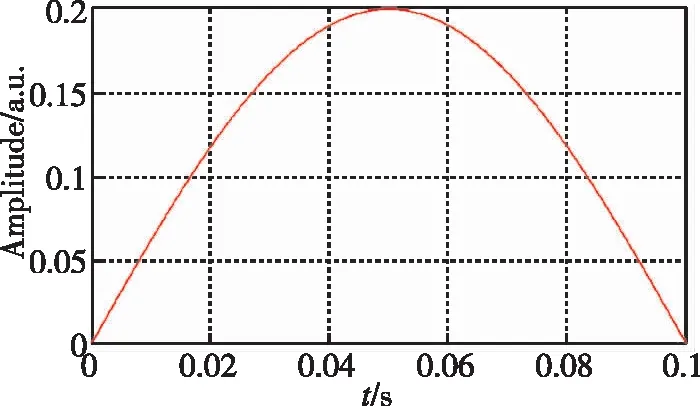
图6 低频干扰信号Fig.6 Low-frequency interference signal

图7 随机噪声干扰信号Fig.7 Random interference signal

图8和图9所示分别为光强在低频干扰信号和随机干扰信号的波动下，传统DCM算法和改进型DCM算法解调结果的对比图。对比图8和图9所示的仿真结果可以看出，光源强度在低频干扰信号和随机干扰信号的波动下，传统DCM算法的解调曲线已经明显失真；而改进型DCM算法的解调曲线基本无失真，较好地实现了对待测信号的复现和还原。

(a)传统DCM算法解调结果

(b)改进DCM算法解调结果图8 低频干扰解调结果对比Fig.8 Demodulation result contrast of low-frequency interference

(a)传统DCM算法解调结果

(b)改进DCM算法解调结果图9 随机干扰解调结果对比Fig.9 Demodulation result contrast of random interference

4 实验验证

按照图10所示的示意图搭建实验系统，激光器选用可调谐半导体激光器，中心波长1550nm。信号发生器分别输出载波调制信号和待测信号。载波调制信号频率为10kHz，待测信号是频率为500Hz的正弦波。2×2耦合器及其尾端的反射镜构成迈克尔逊干涉仪，干涉仪两臂臂长差为3m。光电探测器输出的电信号经过数据采集及处理，最终解调出待测信号。

图10 实验系统示意图Fig.10 Schematic of experiment system

实验中，在光路中引入光强干扰噪声。将采集到的数据分别按照传统DCM算法和改进型DCM算法进行解调，解调结果如图11所示。通过解调结果的对比可以看出，在光源强度受到噪声干扰时，采用传统DCM算法解调的结果已经严重失真，而改进型DCM算法的解调结果能够对待测信号实现更好地解调和复现。实验结果表明，改进型DCM算法能够有效消除光源强度波动的影响，解调性能得到明显提升。

(a)传统DCM算法解调结果

(b)改进DCM算法解调结果图11 解调结果对比Fig.11 Demodulation result contrast

5 结论

本文对干涉型光纤传感器PGC解调技术的DCM算法进行了推导分析，提出了一种抗光强波动的改进型DCM算法。通过仿真和实验结果表明，该改进型DCM解调算法较传统算法可显著提升解调信号的抗光强波动能力，能够有效提高干涉型光纤传感器的工程适应性，对于光纤传感技术的工程应用具有重要意义。