初中数学概括思想的应用分析
山东省汶上县刘楼镇中学 李莹莹
由认识到一些事物的某种属性,特别是本质的属性,推广到认识同类事物的共同属性,这种形成概念的一种思维过程和方法叫作概括。
从以上叙述中,我们发现概括与归纳有某些相同之处,都是从特殊认识一般的思想方法,但不完全如此,二者有本质的区别。
首先,概括是对事物本质属性的认识,数学概念都是在抽象的基础上进行概括而获得的。比如把两条直线相交所成的一类角进行抽象,揭示其本质:两个角的边互为反向延长线,叫作这两个角互为对顶角,并且得出对顶角相等的性质。数学概念都源于概括,如整式与分式、方程、函数、全等三角形等。上课时教师请大家说说“多项式中怎样的项叫同类项?”不是在卖关子,而是教我们学习概括。善于概括方能深刻理解所学的概念,经过自己概括学到的概念,印象特别深刻,不容易遗忘。
其次,概括的对象包括我们进行数学活动的经验,是经验的升华。善于概括方能掌握解决一类问题的基本思路、一般方法。例如经过角平分线上一点,画角平分线的垂线,会产生一个等腰三角形,经历几次后,有的同学就学会了构造这样的等腰三角形辅助解题,这是通过概括才能获得的。具有反思习惯的同学,这样的经验便会越来越多,运用得心应手。
最后,概括是对所学数学知识和方法的提炼。有的同学学了某一章,就能清晰地阐述这一章的主要概念、基本方法、思考策略,这也是概括。华罗庚教授形象地把学习过程比喻成“先把书读厚,再把书读薄”的过程,我的体会是,在消化知识阶段积累越来越多,这就把书读厚了;在理解的基础上能概括出所学知识的精髓,这就把书读薄了。有的教材每一章结束时都选编了若干填空,让同学们回顾知识和方法,这是很有必要的,但还只停留在回顾的水平上。概括的要求更高,还得在此基础上进一步提炼。如果能把各章所学的一系列知识进行概括,对知识的理解将达到更高的水平。
例如把角平分线和线段中垂线的特征,等腰三角形、等腰梯形的判定和性质,圆的垂径定理、切线长定理等,都概括为轴对称图形的性质在不同图形上的体现,就抓住了这些图形的本质,更容易理解这些知识和方法,自觉应用。北师大的曹才翰教授甚至呼吁数学教师,与其说要为迁移而教,不如说要为概括而教,认为概括能力是数学能力的核心。
概括有两种形式:感性概括和理性概括。无论是感性概括还是理性概括,揭示的都是事物的本质属性,所获得的命题都是真命题,而归纳得到的结论就未必是真命题,这也是概括和归纳的重大区别之一。
例1:过点P 画两条直线,与⊙O分别相交于点A、B 和C、D,讨论了∠APC 的度数与它们在⊙O 上截得的两弧AC 和BD 度数的关系。除了点P在圆上,我们把∠APC 叫作圆周角外,另两类角分别称为圆内角和圆外角。请概括:什么样的角叫作圆内角?什么样的角叫作圆外角?它们的度数与所夹弧的度数各有什么关系?
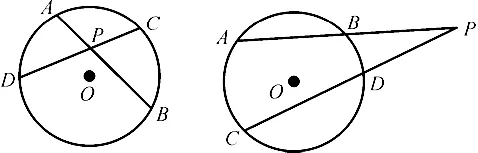
图1
思考:观察图1,圆内角的顶点在圆内,是这个圆的两条弦的交角。因此圆内角的定义是:圆的两条弦相交于圆内一点,这两条弦所夹的角叫作圆内角。(注意:圆的两条弦相交于圆上一点的情况被排除)
类似地,经过圆外一点画圆的两条割线,这两条割线的夹角叫作圆外角。
再把我们计算圆内角、圆外角度数的结论概括如下:
圆内角的度数,等于它与它的对顶角所对的两条弧的度数之和的一半;
圆外角的度数,等于它所夹的两弧度数之差的一半。
请同学们自己证明。
做这道题,要善于反思:联系过去做过的题以及本题的分析,哪些策略具有一般性呢?这就是概括,它能指导我们解决类似的问题。
(1)遇到线段倍、半关系的证明,一般要把较短线段延长1 倍,或构造较长线段的一半,转化为证明两条线段相等;(2)证明两条线段相等,如果它们不在同一个三角形内,常要判定含被证线段的两个三角形全等;(3)观察对称图形是发现等线段、等角的方便途径;(4)证明两个角相等,常常通过它们与第三角的关系来实现。我们许多同学常常感叹上课听得懂,独立解题却束手无策,就是因为我们缺少解题之后的反思,即对解题思路缺少必要的概括,最终不能形成能力。积累经验就是“把书读厚”,概括就是“把书读薄”。

