深度学习视角下的数学课堂教学策略探究
——“平行四边形的面积”的研讨启示
福建省龙岩市松涛小学分校 陈晓招
一、关注已有学情,构建生长的课堂
美国心理学家奥苏泊尔说过:“影响学生学习唯一最重要的因素是学习者已经知道了什么。教学时,要探明这一点,并据此进行教学。”本课学生已经有了用数方格的方法推导面积的经验,因此,课中要把握这一认知起点,唤醒学生的已有经验。与长方形比较,学生眼中的平行四边形属于“不规则图形”。根据前测发现,部分学生会根据已有的学习经验想到通过“移一移”将它转化为长方形来解决,但是对于转化好的长方形与原来平行四边形之间内在的联系则处于模糊状态。也有部分学生根据长方形面积计算方法类比推理出平行四边形面积的计算方法是“底×邻边”。
其实,通过教材分析,我们发现,数方格的作用有二:一是让学生体会面积的本质是面积单位的累加;二是在数方格的过程中蕴含转化思想,为后续的剪拼法搭好架子。有了这个认识,在教学设计时才会重视方格纸的使用,并发挥其作用,让学生从数方格的方法成功过渡到剪拼法,构建生长的课堂。
二、把握知识本质,构建深度关联的课堂
深度学习就意味着对知识本质的理解,意味着对知识内在联系与建构的把握,意味着迁移与应用。几何的学习不等于计算,学生在周长和面积的应用时往往对公式脱口而出,但是对于“公式”为什么是这样的知之甚少。本课应着力于让学生明白公式的来龙去脉。我尝试将小学阶段6 种平面图形的面积用一个公式串联,让学生的探究有深度、有力度,这个公式就是“每行面积单位个数×行数”。本课从回顾长方形面积的计算方法入手,唤醒学生数方格算面积的学习经验,学生在迁移类比中发现,平行四边形转化为长方形的本质就是为了方便计算“每行面积单位个数×行数”。
【片段1】
师:方格纸已经为大家准备好,独立思考,通过数一数、移一移的方法,得出平行四边形的面积。
生1:
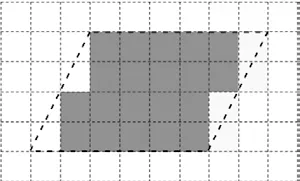
生2:

师:你们为什么要这样移动呢?
生:好算。
生:移完之后,就都是满格的,每行有6 格,正好有4 行。
师:回顾刚才的几种做法,他们都是把不完整的格子数转化为完整的格子数,与长方形面积一样,用每行格子数乘行数。
【片段2】
课末:
师:同学们,你们还想研究哪些图形的面积呢?
生:三角形、梯形、四边形、圆形……
师:那么你觉得用今天的学习经验可以解决这些问题吗?
生:可不可以用数方格的方法?

借助微课,从两方面对本节课的要点进行梳理:一是知识本质层面。用“每行面积单位个数× 行数”一个式子将小学阶段所有平面图形面积的探究进行串联,让知识由“厚”变“薄”。二是思想方法层面。引导学生将“转化”这一思想应用在后续平面图形面积的探究中,两个层面的梳理实现了知识结构化、方法结构化。
三、渗透数学思想,构建有经验的课堂
史宁中教授说:“数学思想是学过数学的人特有的思维能力。”数学课堂教学除了知识技能的掌握,更重要的是使学生习得学法,提高思维能力。教师要把握好知识技能这一“明线”,更要重视思想方法这一“暗线”,构建有思想的课堂、有方法的课堂、有经验的课堂。
本课中,如何引导学生有效体悟“转化”这一思想方法呢?本课可以设计两次操作:第一次,在方格纸中,将不完整的格子变成完整的格子;第二次,学生将心目中的不规则图形——平行四边形变成规则的长方形。教师要巧妙地将学生两次的体会沟通联系,使学生对“转化”这一数学思想方法有更深刻的体悟。这一体悟对后续的学习具有重要作用。因为学生在学习三角形、梯形的面积时,往往受平行四边形面积学习经验的影响,很难主动想到要用两个完全一样的三角形来推导,只会想到在单个图形中剪拼。本课中学生对于“转化”思想的深刻体会,有利于学生思考:怎样才能将三角形转化成学过的平行四边形或长方形呢?使得“需要两个完全一样的三角形”成为学生自然的想法。由“割补”到“拼摆”,这是学生应用“转化”思想方法解决问题的一个突破。
四、关注过程体验,构建探究式的课堂
每个学生的数学知识基础不同、思维方式不同,学生面对问题所使用的思考策略必然呈现群体上的多样化。课堂教学应尊重学生的体验,尊重学生的个性化学习。鼓励学生猜想、操作、思考,学生在“数一数、移一移、剪一剪、拼一拼、议一议、说一说”等活动过程中充分展示个性想法。教师提供展示的平台,启迪学生深思,引发思维碰撞,实现有效的探究学习。
【片段】
首次验证:
师:平行四边形的面积怎样计算?
生1:用这两条边乘在一起。(手指邻边)
师:这两条边是邻边,你的意思是邻边相乘。(板书)
生2:我觉得是底乘高。
师板书。
师:现在全班同学有了两种猜想,到底哪种对呢?怎么办?
生:验证一下。
师:你想怎么做?
生:刚才长方形的面积是数方格的,看看平行四边形的面积能不能也数出来。
师:有想法。动手试试吧!
生反馈(略)
……
再次验证:
师:通过数方格,同学们验证了这个平行四边形的面积是底乘高。还有什么疑问吗?
生:除了数方格,还有更简单的方法吗?
生:底乘邻边为什么不可以呢?
生:是不是所有的平行四边形面积都等于底乘高呢?
师:太棒了,提出了这么多有研究价值的问题。你们想怎么做?
生:要各种各样的平行四边形。
生:刚才在数方格的时候我发现平行四边形都可以把这一小块剪下来,拼成长方形,所以我觉得平行四边形的面积是长乘宽。
师:大家拿出学具袋动手试试吧,把你的发现与同桌说一说。
给学生不同形状的平行四边形,目的是让学生经历从特殊到一般的归纳过程。在动手操作的基础上引导学生深度说理,配上课件的直观演示,公式的推导水到渠成。学生在“变”与“不变”中发现两个图形的内在联系,亲历了知识形成的过程,既培养了学生的学习能力,又让他们体验到成功的喜悦。
五、结语
总之,深度学习的课堂应该让学生体会到知识的系统化与条理化,从系统梳理到整体结构化地把握知识,引导学生寻找知识间的差异到沟通知识间的内在联系,从个性化整理到创造性呈现,学生对整个过程的经历与体验有深度、有广度,这样的课堂有利于学生形成综合学习能力,加大学习的深度与广度,发展数学核心素养。

