单轴应力下的孔洞–裂隙扩展规律数值模拟

郭修成

单轴应力下的孔洞–裂隙扩展规律数值模拟

郭修成

(长城钻探工程有限公司工程技术研究院，辽宁 盘锦 124010)

为研究不同孔洞–裂隙(简称“孔–隙”)赋存条件下的裂纹扩展规律，利用RFPA软件，对不同裂纹倾角及不同非均质系数下的岩体破坏进行数值模拟分析，获得其裂纹扩展过程、声发射规律、应力–应变曲线，同时与原试验结果进行对比验证。结果表明：完整试样裂纹沿着剪切方向产生，含孔–隙试样裂纹沿裂隙尖端及孔口侧边产生；翼裂纹贯穿试件的同时，在预制裂纹尖端或孔口侧边产生水平方向的次生裂纹，并产生分叉，非均质系数影响次生裂纹走向；压载前期试样以拉破坏为主，压载后期以拉–剪组合破坏为主，次生裂纹的产生与剪切破坏有关；声发射累计能量与声发射累计数前期缓慢增大，后期迅速增大，预制裂纹倾角越小，非均质系数越大，声发射累计能量越大；不同裂纹倾角及不同非均质系数试件的应力–应变曲线均经历3个阶段：弹性变形阶段、非线性变形阶段及残余变形阶段，孔–隙的存在降低了试样的峰值强度，影响试件的脆性度。研究结果为进一步认识孔–隙相互作用规律提供了参考。

单轴应力；孔–隙作用；声发射；裂纹扩展；应力–应变曲线；数值模拟

孔洞、裂隙广泛存在于岩体内部[1-3]，如深埋隧洞在孔洞周围存在大量的裂隙，在复杂应力下裂隙与裂隙、裂隙与孔洞及孔洞与孔洞之间会扩展贯通[4-6]，当达到极限状态时，岩体结构将发生灾变，因此，对岩体缺陷的力学规律研究将有益于认识及防治岩体灾变。

国内外对含缺陷(包括裂隙及孔洞)岩体的力学规律研究较多，陈雪峰等[6]开展了不同厚度节理爆破模型试验，得到节理模型的裂纹扩展规律；王飞等[7]对平行节理相互作用下岩体的力学性能进行了室内实验；岳中文等[8]对含切槽炮孔的脆性岩体在爆破作用下的动态裂纹扩展进行了研究；李竟艳等[9]基于Abaqus软件对动态拉伸载荷下岩石材料泛形裂纹扩展进行了数值模拟研究；李宏等[10]基于离散元颗粒流程序PFC对含非贯通型表面裂隙组的试件进行了分析，得到含多组裂隙相互贯通扩展的规律；周喻等[11]对含不同方位角的双圆孔类岩石试件进行了单轴压缩试验，得到双孔的相互作用规律。以往研究均仅针对裂隙与裂隙之间或孔与孔之间的裂纹扩展规律，对裂隙与孔之间裂纹的扩展规律研究较少。

本文利用RFPA软件，采用数值模拟方法，对不同非均质系数、不同方位角下的裂纹扩展过程、应力–应变曲线及声发射规律进行分析，将模拟结果与原试验结果进行对比，验证数值模拟结果的合理性，研究成果为认识孔–隙相互作用规律提供参考。

1 数值模拟计算理论

1.1 单轴压缩下脆性材料的破坏准则

裂隙在受到双轴应力作用下，Griffith理论强度[12-18](裂隙发展理论)可以写成：

式中：1、3分别为最大、最小主应力，MPa；t为抗拉强度，MPa。

若岩体受到单向压缩，则3=0，1=c，c表示单轴抗压强度，MPa，可得：

将Griffith理论写成Moh-Coulomb形式，可以将式(2)用正应力和剪应力表示，即：

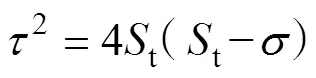
式中：、分别为裂纹上的正应力与切应力，RFPA软件正是根据这一理论进行模拟计算。

1.2 岩石介质非均匀性的统计理论

非均质系数可描述岩体材料的不均匀程度。对于同一种岩石材料来说，矿物晶体、胶结物晶体及各种微缺陷等具有各自的排列方式，相互之间结合强度有差异，导致其物理性质不能用同一特征值描述。1939年，Weibull率先提出用统计数学描述材料非均匀性的方法，Weibull统计分布函数表达式[11]可表示成：

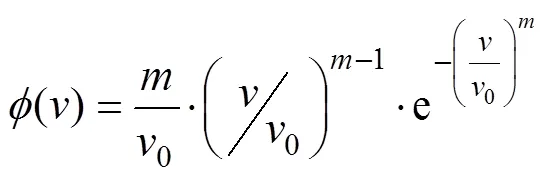
式中：为岩石介质的基元体力学性质参数(强度、弹性模量等)；0为基元体力学性质的平均值；为分布函数的非均质系数，反映岩石介质的均质性；()为岩石基元体力学性质的统计分布密度。

本文对于岩石不均匀程度的描述采用本节非均质系数定义。

1.3 RFPA系统的基元状态定义及计算流程

1.3.1 RFPA基元状态定义

RFPA中的基元系统指在模型中当前功能的实体介质，它的本构关系由应力应变关系及破坏准则式(3)所描述。脆性介质最大特点之一是介质的变形达到某个阈值时，介质的力学性质将发生突变，即介质由于损伤而导致其承载力急剧下降，甚至完全丧失承载力，基元将发生相变。

RFPA中将压、剪破坏引起的基元破坏称为Ⅰ类相变，将拉应力引起的基元破坏称为Ⅱ类相变。当基元介质发生相变后，RFPA引入空气单元的概念，由于空气单元的基元弹性模量极低，可近似认为实体介质的力学行为已不再存在，这样，在不改变模型数学结构的前提下，使模型在总体特性上可以反映因基元破裂而引起的物理特性改变。值得注意的是，对于已形成的裂纹面(即空气单元)，当裂隙两面的介质在压应力作用下出现压密或压实的现象时，将空气单元改为接触单元，使其刚度增大，起到传递应力的作用，这就是所谓的接触单元特性。

1.3.2 RFPA计算流程

a. 建模及网格 可以根据用户需要选择基元(分为实体、支护、孔洞)，网格采用自动剖分技术。

b. 应力应变计算 根据输入的边界条件，进行有限元计算，输出应力、应变及位移信息。

c. 相变分析 根据式(1)—式(3)判断单元是否发生相变，进行基元的转化处理。

2 裂纹扩展数值计算模型

2.1 模型及参数

为研究不同裂纹方位角及不同非均质系数下含孔洞裂隙试件在单轴压力下的裂纹扩展规律，根据文献[19]的试验结果进行有限元建模计算。数值模拟采用二维试样模型，宽60 mm，长120 mm，采用平面应力模型，圆孔布置于试件中心，圆孔半径为5 mm，孔洞侧边裂隙长度为12 mm，裂隙倾角定义为裂隙方向与水平方向的夹角，计算模型如图1a所示；不同材料非均质系数=1.1、3、5、10、50的弹性模量分布如图1b—图1f所示。试样采用单轴压缩应力加载，加载速率设置为0.004 mm/步；材料的基础参数见表1。

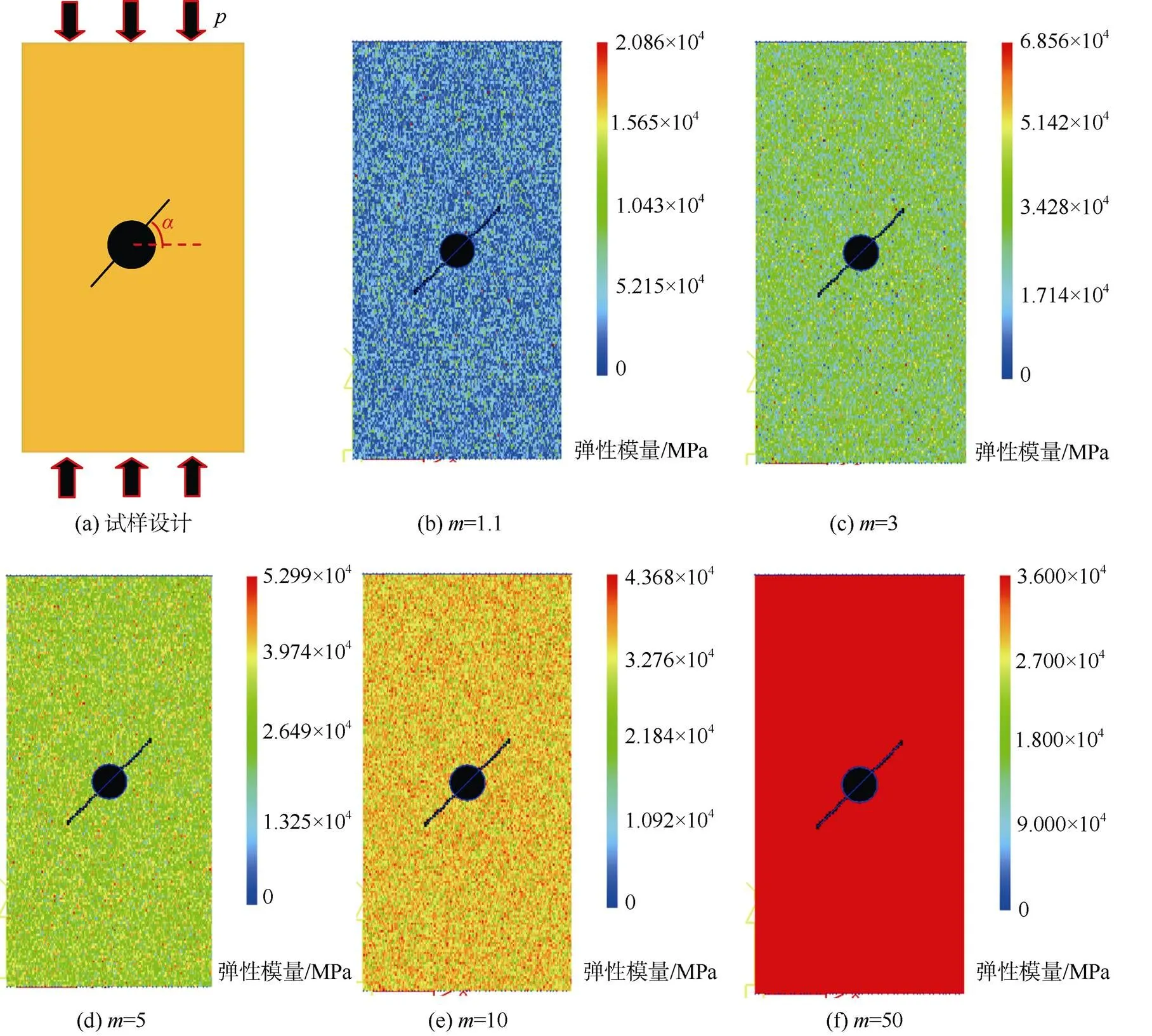
图1 试样设计及不同非均值系数下的弹性模量分布

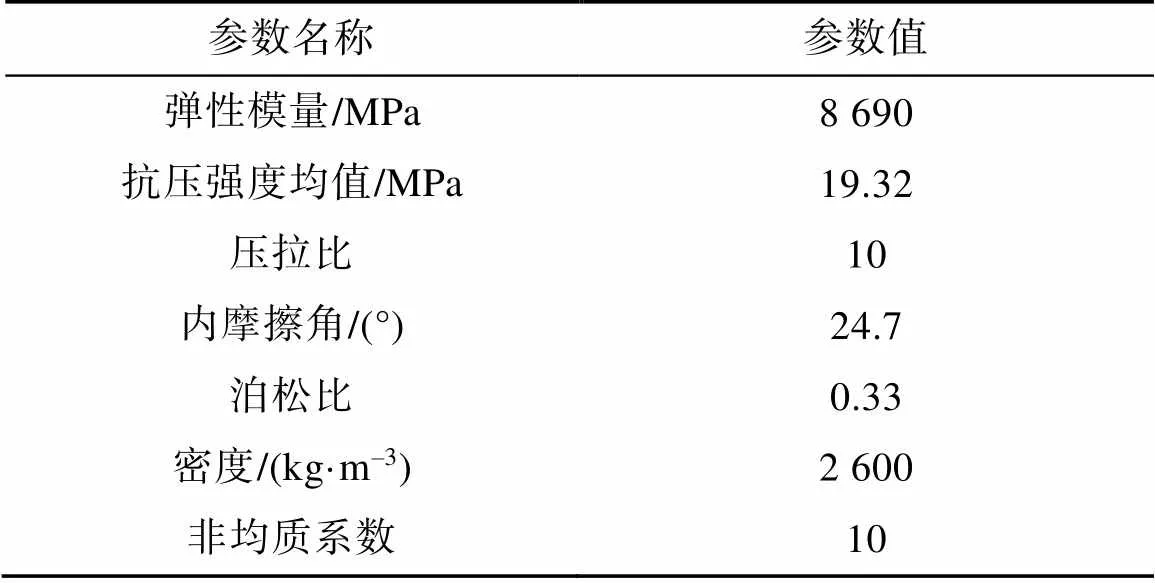
表1 材料基础参数

2.2 模拟计算工况

为研究不同裂隙倾角及不同非均质系数下的孔–隙相互作用规律及对材料物理力学性质的影响，设置5个计算工况：①工况1，完整对比组，目的是与含孔洞及裂隙试件的对比研究；②工况2，不同裂隙倾角组，目的是对比不同裂隙倾角下试件物理力学特性差异；③工况3，不同非均质系数组，目的是对比不同非均质系数对试件物理力学特性的影响；④工况4，含单孔试样组，目的是与多孔试样进行对比分析；⑤工况5，含单裂隙试样组，目的是与含孔–隙试样进行对比分析，具体计算工况详见表2。

3 模拟计算结果分析

3.1 裂纹扩展过程

3.1.1 工况1、工况2及工况4

完整试样的裂纹扩展计算过程与含孔洞及裂隙试样的裂纹扩展过程如图2所示。由图2可知，孔–隙的存在及裂纹倾角对试件破坏形态有较大影响，主要规律体现如下。

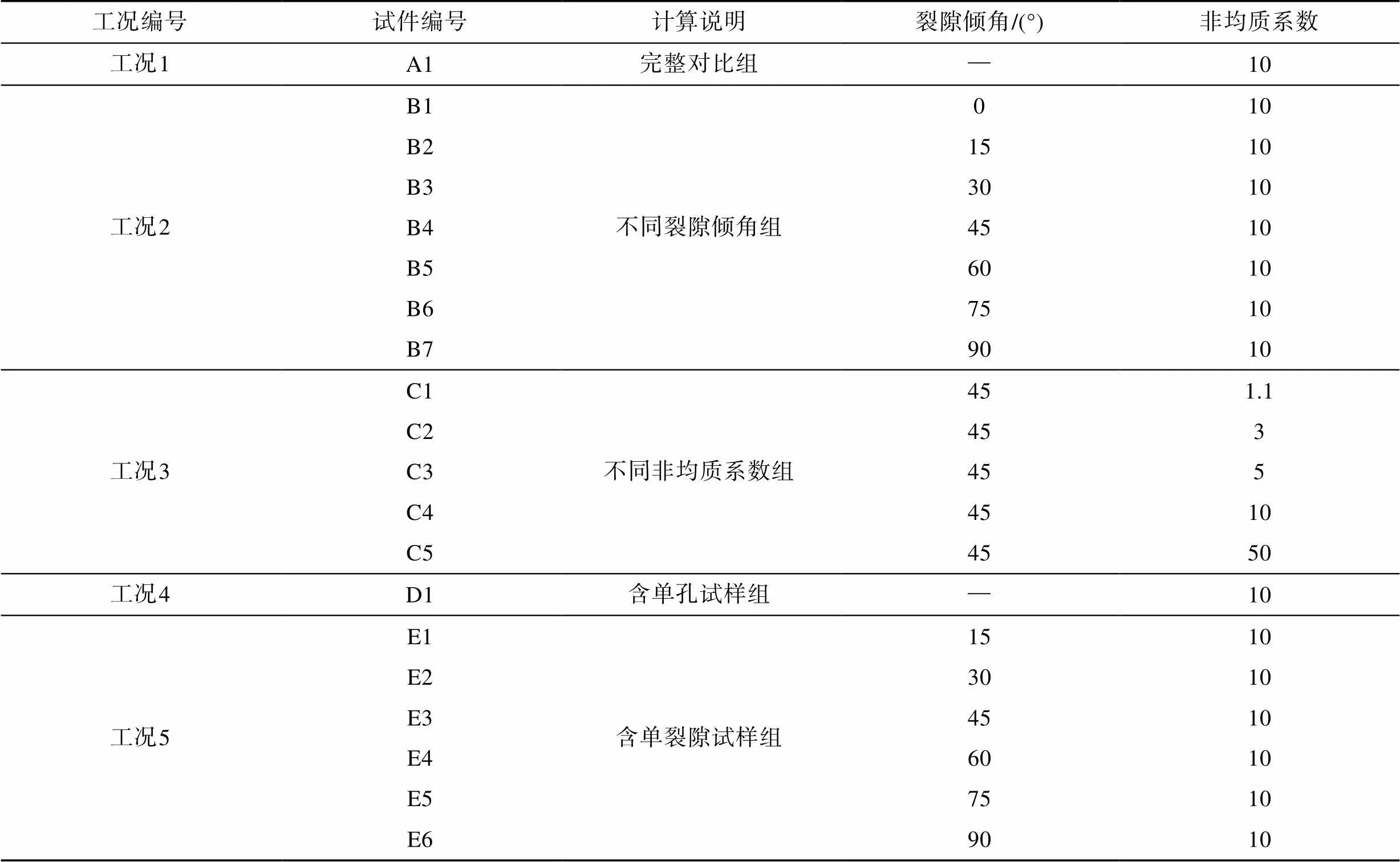
表2 不同裂隙倾角及非均质系数的计算工况

对于完整试样来说，试件呈现典型的剪切破坏模式，即剪切破坏面沿试件约60°方向产生(图2a)。对单含孔洞试样而言，裂纹首先在孔洞上下出现，随后出现剪切裂纹，使试样呈现典型的剪切破坏模式(图2b)。预制裂纹倾角较小时(=0°,15°,30°)，裂纹首先沿着孔口上下端产生，并持续扩展；当裂隙倾角为30°时，在预制裂纹下端产生翼裂纹，最终裂纹沿着最大主应力方向发展并贯穿试件(图2c—图2e)；值得注意的是，裂纹扩展过程中产生一定的分叉，同时，在裂纹扩展后期预制裂纹尖端产生次生裂纹，次生裂纹沿水平方向发展，并产生更大的裂纹分叉。当预制裂纹倾角较大时(=45°,60°)，翼裂纹首先沿预制裂纹尖端产生，并沿最大主应力发展，未在孔口上下顶端产生；最终翼裂纹贯穿试件的同时在预制裂纹尖端产生水平方向的次生裂纹，并产生更大的分叉(图2f,图2g)。当预制裂纹倾角很大时(=75°,90°)，翼裂纹产生于预制裂纹尖端，但次生裂纹产生于孔口左右侧顶端(图2h—图2i)。

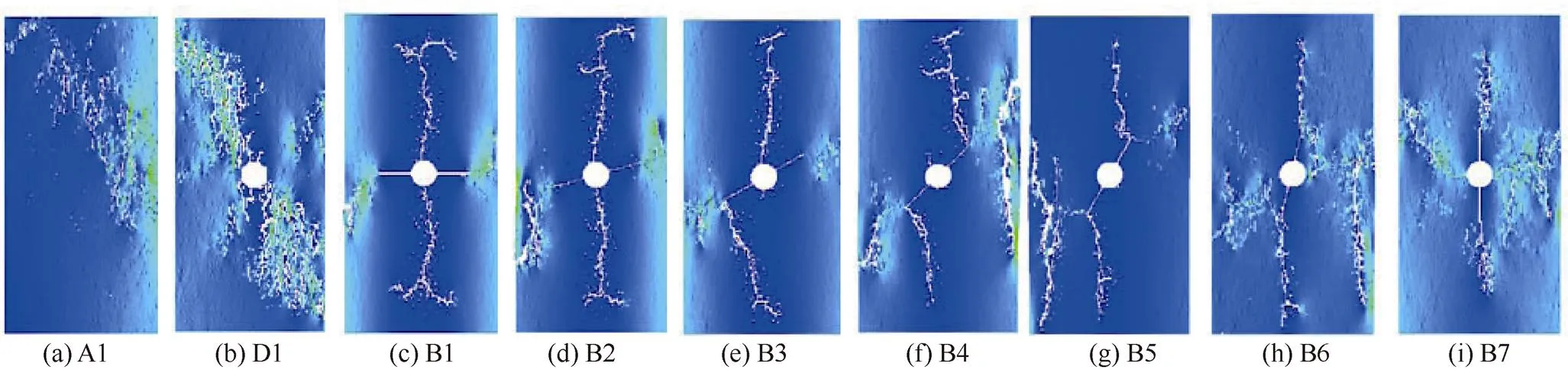
图2 工况1、工况2与工况4裂纹扩展过程

3.1.2 工况3

不同非均质系数下的试件裂纹扩展过程如图3所示。由图3可知，不同非均质系数下的孔–隙裂纹扩展规律也有一定差异。

不同非均质系数下，翼裂纹首先在预制裂纹尖端处产生，并逐渐沿着最大主应力方向发展，非均质系数越大，裂纹分叉程度就越弱。不同非均质系数下的次生裂纹形态也有不同，当非均质系数较小时(=1.1)，次生裂纹形态为反翼裂纹，即次生裂纹扩展方向与翼裂纹扩展方向相反(图3a)；而非均质系数较大时(=3,5,10,50)，次生裂纹扩展则主要沿着水平方向进行扩展(图3b—图3e)。

3.1.3 工况5

含单裂隙不同倾角下的试件裂纹扩展过程如图4所示。由图4可知，不同裂隙倾角下的裂纹扩展规律与含孔–隙试样的裂纹扩展规律大有不同，裂隙的分叉效应更加明显，当裂隙的倾角较小时(=0°,15°)，裂纹从预制裂隙的中部产生(图4a)；当预制裂隙的倾角较大时(大于30°)，裂纹将从预制裂隙的尖端产生，随后朝着最大主应力方向发展，最终使得试样破坏。

图3 不同非均质系数下的裂纹扩展过程

图4 不同裂隙倾角下的裂纹扩展过程

3.2 声发射规律分析

3.2.1 工况1、工况2及工况4

完整试件与含不同倾角裂隙及孔洞试件的声发射过程及声发射曲线如图5—图6所示。在RFPA中，白色圆圈代表发生剪切破坏，红色圆圈代表发生拉伸破坏。

由图5可知，声发射规律与3.1节裂纹扩展规律呈现高度的一致性，主要得出以下规律。

对于完整试样来说，声发射事件首先无规律分布于试件的不同部位，这是由试件的非均质性导致；在压载后期，沿剪切方向产生拉剪复合破坏，声发射事件也集中于此区域(图5a)。

对于单含孔洞试样而言，声发射事件首先在孔口上下集中，为拉破坏；随后沿剪切方向产生，为拉剪复合破坏(图5b)。

对于含孔–隙试件来说，声发射事件首先在孔口两侧或预制裂纹尖端产生拉破坏，在压载一段时间后产生剪切破坏，且剪切破坏主要沿着次生裂纹的扩展方向，可见次生裂纹主要是由剪切破坏产生(图5c—图5g)；对于倾角较大的情况而言(图5h—图5i)，由于预制裂隙的倾角较大，剪切裂纹则从孔洞周围产生。

声发射能量与声发射事件随计算步呈现前期缓慢增大，后期迅速增大的规律，且预制裂纹的倾角越小，声发射的累计能量越大(图6)。

3.2.2 工况3

不同非均质系数下的声发射规律如图7—图8所示。由图可见，不同非均质系数的声发射规律和累计能量曲线与前述规律较为类似，值得注意的是，非均质系数越大，声发射的累计能量也越大。

3.3 应力应变分析

不同试样的应力–应变曲线如图9所示。

由图9可知，不同裂纹倾角及不同非均质系数试件的应力–应变曲线均经历3个阶段：

a.弹性变形阶段 此阶段应力随应变基本上呈线性分布；

b.非线性变形阶段 此阶段应力–应变曲线偏离线性变形，主要是由于随着岩体内部随机分布的相变基元数量的增加和局部裂纹的形成，岩石试件的弹性模量逐渐降低；

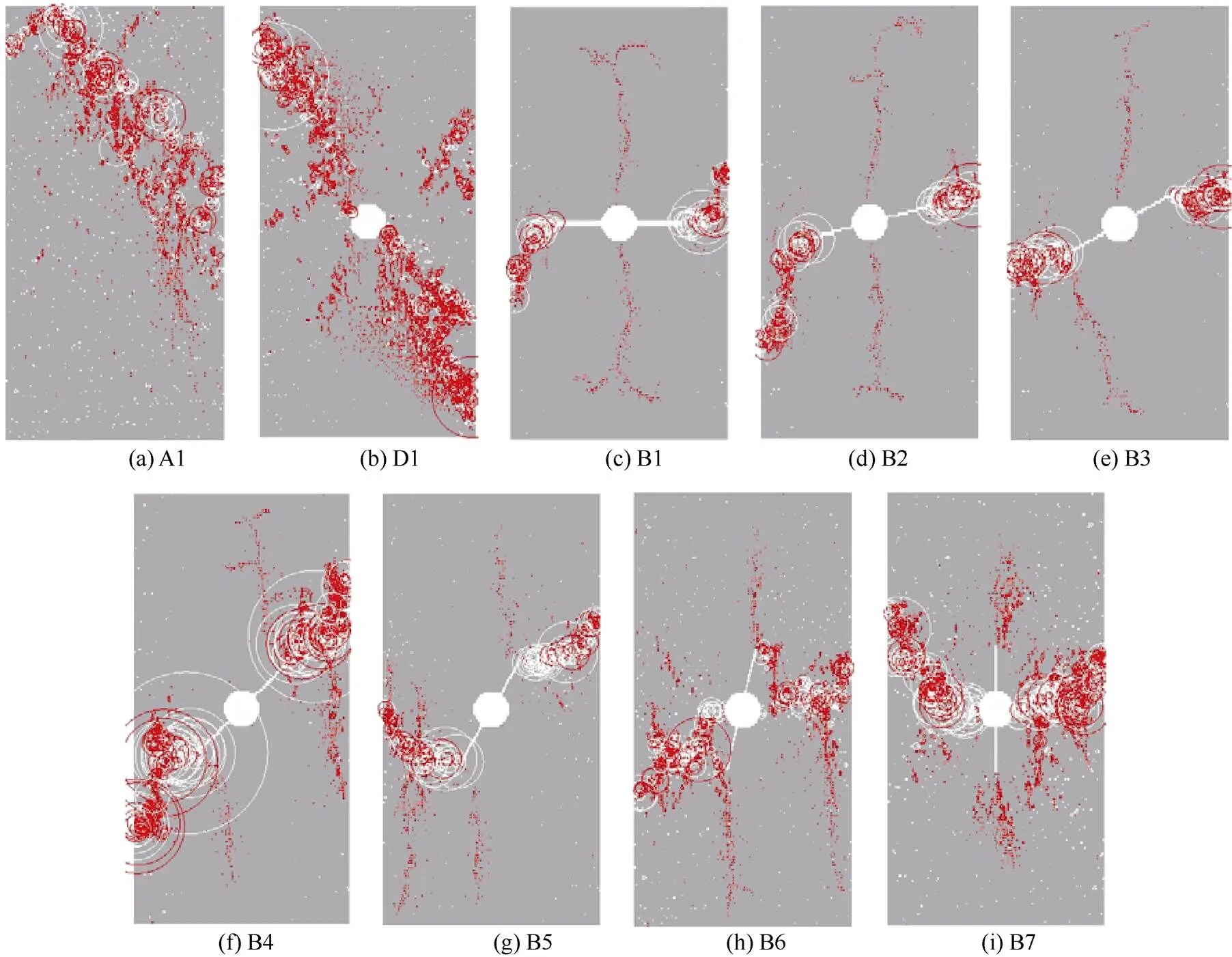
图5 工况1、工况2及工况4声发射规律

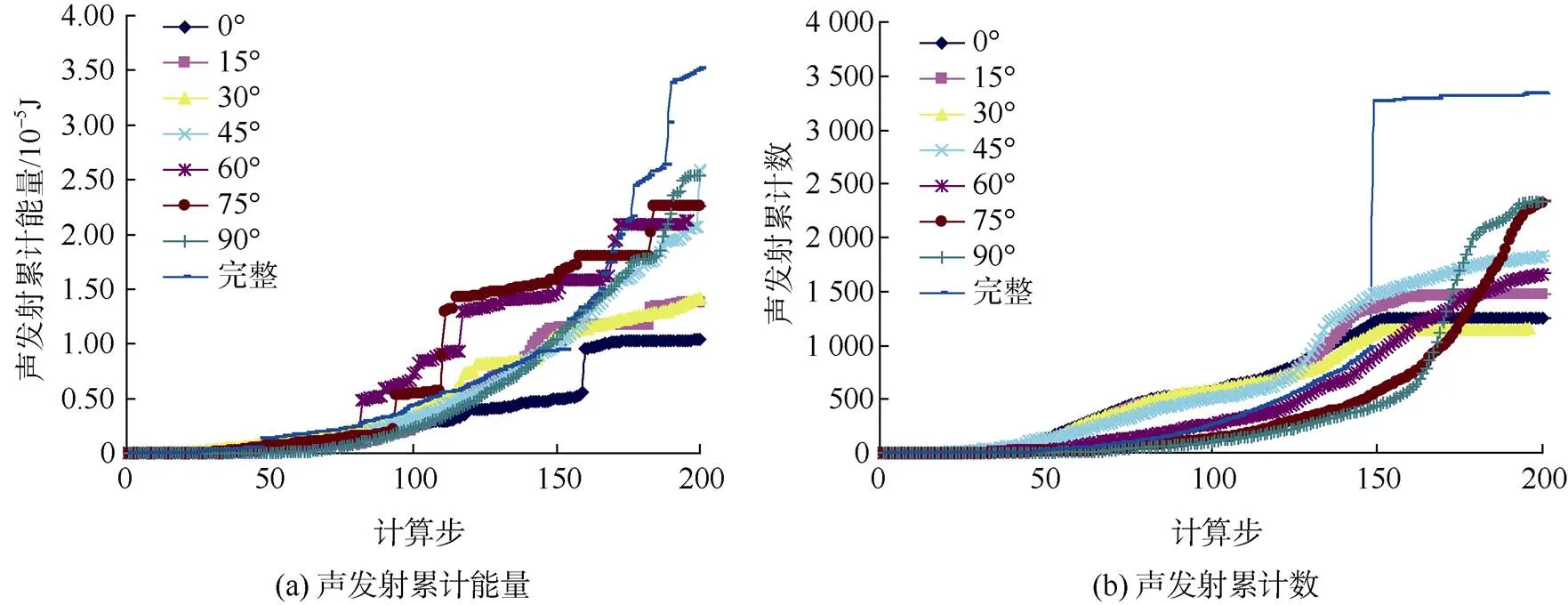
图6 声发射累计能量与声发射累计数(m=10)

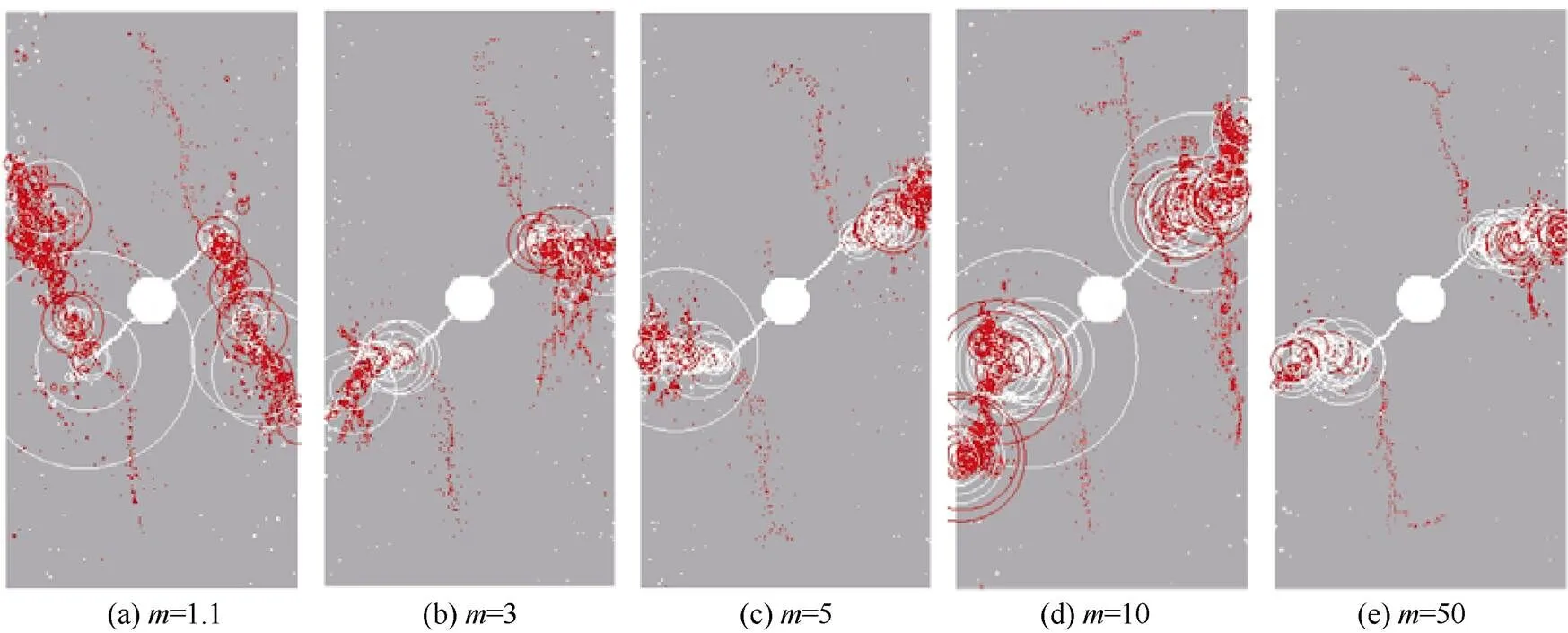
图7 不同非均质系数下的声发射规律

图8 声发射累计能量与声发射累计数(45°)

c.残余变形阶段 此阶段应力水平较低，但是变形较大，试件形成宏观剪切面。

不同非均质系数对试样的应力–应变曲线影响较小，但对不同孔–隙形式影响较大：

①孔–隙的存在极大地降低了试样的峰值强度，且预制裂隙倾角越小，试样的强度降幅越大；

②孔–隙的存在同时降低了试样整体的脆性度，完整试样的应力–应变曲线呈典型的脆性破坏模式，即试样到达峰值荷载时应力呈现“断崖式”跌落(图9a)，含孔–隙试样则具有一定的峰后特征，且预制裂隙倾角越小，延性破坏特征越明显。

4 与现有研究成果对比

为验证本文数值模拟的合理性，将模拟结果与本文计算模型的原试验结果[19]进行对比。文献[19]选用典型的砂岩作为试验材料，试样尺寸为120 mm× 60 mm×30 mm，孔洞直径=10 mm，孔洞两侧裂隙长度2=2=12 mm，裂隙倾角为45°，采用单轴压缩加载方式，加载速率为4×10–6m/s，加载至试样破坏，最终破坏形态如图10a所示；图10b为本文的数值模拟结果。由图10可知，数值模拟与原试验结果呈较好的一致性，即产生了翼裂纹与次生裂纹；同时，裂纹产生位置也有较好的对应性，从而验证了本文数值模拟的合理性。

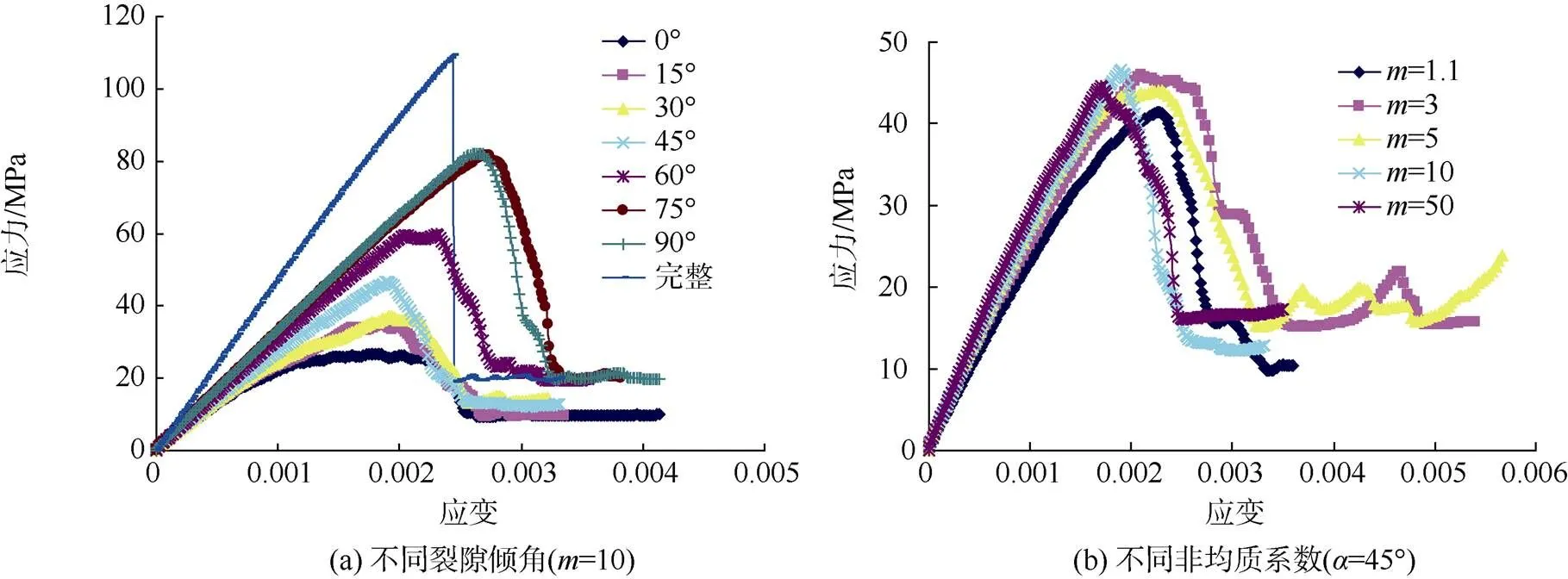
图9 不同试样的应力–应变曲线

5 结论

a. 剪切裂纹产生于完整试样，裂纹尖端及孔口拉裂纹出现在含孔–隙试样，裂纹倾角与非均质系数对裂纹扩展影响巨大。

b.拉伸破坏发生在受载前期，而拉–剪破坏则出现在后期，声发射数及能量前期增速较慢，后期迅速加快，预制裂纹倾角与声发射累计能量呈负相关，而非均质系数则相反。

c. 受载下的应力–应变曲线均经历3个阶段：弹性变形阶段、非线性变形阶段及残余变形阶段，孔–隙的存在降低了试样的峰值强度，影响试件的脆性度。

d. 将数值模拟结果与原试验结果进行对比，裂纹扩展发生在预制裂纹尖端与孔口周围，试验结果与数值模拟结果一致，验证了数值模拟结果的可靠性。

图10 数值模拟与试验结果的对比

e. 预制裂纹倾角小于30°时，裂纹从预制裂隙的中部产生，大于30°时裂纹从预制裂纹尖端产生；非均质系数越大，裂纹扩展分叉越少。

请听作者语音介绍创新技术成果等信息，欢迎与作者进行交流

[1] 冯彦军，康红普. 受压脆性岩石Ⅰ–Ⅱ型复合裂纹水力压裂研究[J]. 煤炭学报，2013，38(2)：226–232.FENG Yanjun，KANG Hongpu. The initiation ofⅠ-Ⅱmixed mode crack subjected to hydraulic pressure in brittle rock under compression[J]. Journal of China Coal Society，2013，38(2)：226–232.

[2] 严鹏，陈拓，卢文波，等. 岩爆动力学机理及其控制研究进展[J]. 武汉大学学报(工学版)，2018，51(1)：1–14. YAN Peng，CHEN Tuo，LU Wenbo，et al. A review of dynamic mechanism and controlling of rock burst[J]. Journal of Wuhan University(Engineering Edition)，2018，51(1)：1–14.

[3] 郭建强，刘新荣. 强度准则与岩爆判据统一的研究[J]. 岩石力学与工程学报，2018，37(增刊1)：3340–3352. GUO Jianqiang，LIU Xinrong. Study on the uniformity between strength criterion and rock burst criterion[J]. Journal of Rock Mechanics and Engineering，2018，37(S1)：3340–3352.

[4] 郭品坤. 煤与瓦斯突出层裂发展机制研究[D]. 徐州：中国矿业大学，2014. GUO Pinkun. Research on laminar spallation mechanism of coal and gas outburst propagation[D]. Xuzhou：China University of Mining and Technology，2014.

[5] 刘瑞峰，朱哲明，刘邦，等. 爆炸载荷下砂岩动态断裂特性的试验研究[J]. 岩石力学与工程学报，2019，38(3)：445–454.LIU Ruifeng，ZHU Zheming，LIU Bang，et al. Experimental study on dynamic fracture characteristics of sandstones under blasting[J]. Journal of Rock Mechanics and Engineering，2019，38(3)：445–454.

[6] 陈雪峰，赵孝学，汪海波，等. 节理充填岩体爆炸应力波传播规律模型试验与应用研究[J]. 中国安全生产科学技术，2018，14(12)：130–134. CHEN Xuefeng，ZHAO Xiaoxue，WANG Haibo，et al. Model tests and application research on propagation laws of blasting stress wave in jointed and filled rock mass[J]. Journal of Safety Science and Technology，2018，14(12)：130–134.

[7] 王飞，曹平，曹日红，等. 平行节理相互作用对节理岩体的力学行为影响[J]. 中南大学学报(自然科学版)，2018，49(10)：2498–2507. WANG Fei，CAO Ping，CAO Rihong，et al. Influence of parallel joint interaction on mechanical behavior of jointed rock mass[J]. Journal of Central South University(Science and Technology)，2018，49(10)：2498–2507.

[8] 岳中文，邱鹏，杨仁树，等. 切槽炮孔偏心装药爆源近区裂纹动态力学特征实验研究[J]. 岩石力学与工程学报，2017，36(增刊2)：3792–3798.YUE Zhongwen，QIU Peng，YANG Renshu，et al. Experimental study on crack dynamic mechanical characteristic near blasting source of grooved borehole with eccentric decouple charge[J]. Journal of Rock Mechanics and Engineering，2017，36(S2)：3792–3798.

[9] 李竟艳，高文学，宋肖龙. 岩石材料动载下泛形裂纹扩展数值模拟[J]. 振动与冲击，2018，37(22)：88–91. LI Jingyan，GAO Wenxue，SONG Xiaolong. Numerical simulation on the extension of a ubiquitiformal crack of rock materials under dynamic loading[J]. Journal of Vibration and shock，2018，37(22)：88–91.

[10] 李宏，张丽萍，邓清海，等. 非贯通裂隙岩体的单轴压缩颗粒流数值模拟[J]. 水力发电，2018，44(11)：26–30.LI Hong，ZHANG Liping，DENG Qinghai，et al. Numerical simulation of uniaxial compression particle flow in non-penetrating fractured rock mass[J]. Water Power，2018，44(11)：26–30.

[11] 周喻，刘冰，王莉，等. 单轴压缩条件下含双圆孔类岩石试样力学特性的细观研究[J]. 岩石力学与工程学报，2017，36(11)：2662–2671. ZHOU Yu，LIU Bing，WANG Li，et al. Mesoscopic mechanical properties of rock-like material containing two circular holes under uniaxial compression[J]. Journal of Rock Mechanics and Engineering，2017，36(11)：2662–2671.

[12] 章广成，胡静. 非贯通单节理岩体裂纹扩展方向研究[J]. 煤田地质与勘探，2011，39(4)：43–48. ZHANG Guangcheng，HU Jing. Study on crack propagation direction of intermittent single jointed rock mass[J]. Coal Geology & Exploration，2011，39(4)：43–48.

[13] 张力民，张慧，刘红岩. 单轴压缩荷载下非贯通闭合节理岩体损伤本构模型[J]. 煤田地质与勘探，2016，44(1)：79–84. ZHANG Limin，ZHANG Hui，LIU Hongyan. A damage constitutive model for rock mass with non-persistently closed joints under uniaxial compression load[J]. Coal Geology & Exploration，2016，44(1)：79–84.

[14] 姚改焕，宋战平，余贤斌. 石灰岩声发射特性的试验研究[J].煤田地质与勘探，2006，34(6)：44–46. YAO Gaihuan，SONG Zhanping，YU Xianbin. Experimental study on acoustic emission characteristics of limestone[J]. Coal Geology & Exploration，2006，34(6)：44–46.

[15] 骆中山，曹函，孙平贺，等. 水力压裂脉冲频率对煤岩预制孔密封效果影响[J]. 煤田地质与勘探，2018，46(2)：190–195. LUO Zhongshan，CAO Han，SUN Pinghe，et al. Influence of hydraulic fracturing pulse frequency on precasting sealing effect of coal rock[J]. Coal Geology & Exploration，2018，46(2)：190–195.

[16] 张帆，马耕，刘晓，等. 煤岩水力压裂起裂压力和裂缝扩展机制实验研究[J]. 煤田地质与勘探，2017，45(6)：84–89. ZHANG Fan，MA Geng，LIU Xiao，et al. Experimental study on initiation pressure and mechanism of fracture propagation of hydraulic fracturing in coal and rock mass[J]. Coal Geology & Exploration，2017，45(6)：84–89.

[17] 李地元，成腾蛟，周韬，等. 冲击载荷作用下含孔洞大理岩动态力学破坏特性试验研究[J]. 岩石力学与工程学报，2015，34(2)：249–260. LI Diyuan，CHENG Tengjiao，ZHOU Tao，et al. Experimental study of the dynamic strength and fracturing characteristics of marble specimens with a single hole under impact loading[J].Journal of Rock Mechanics and Engineering，2015，34(2)：249–260.

[18] 王蒙，朱哲明，谢军. 岩石Ⅰ–Ⅱ复合型裂纹动态扩展SHPB实验及数值模拟研究[J]. 岩石力学与工程学报，2015，34(12)：2474–2485. WANG Meng，ZHU Zheming，XIE Jun. Experimental and numerical studies of the mixed-modeⅠandⅡcrack propagation under dynamic loading using SHPB[J]. Journal of Rock Mechanics and Engineering，2015，34(12)：2474–2485.

[19] 程龙，杨圣奇，刘相如. 含缺陷砂岩裂纹扩展特征试验与模拟研究[J]. 采矿与安全工程学报，2012，29(5)：719–724. CHENG Long，YANG Shengqi，LIU Xiangru. Experimental and numerical investigation on crack expansion of sandstone containing flaws[J]. Journal of Mining & Safety Engineering，2012，29(5)：719–724.

Numerical simulation of propagation law of pore-fracture under uniaxial stress

GUO Xiucheng

(Engineering and Technology Research Institute of Great Wall Drilling Engineering Co. Ltd., Panjin 124010, China)

In order to study the law of crack propagation under different pore-fracture conditions, the crack propagation process, acoustic emission law and stress-strain curve under different crack inclination angle and different heterogeneous coefficient were numerically simulated by using RFPA software. At the same time, the results are compared with the experimental results. The results show that the cracks of the intact specimen are produced along the shear direction, while the cracks of the specimens with pores occur along the side of the crack tip and the orifice. The secondary cracks in horizontal direction and bifurcation at the prefabricated crack tip or the side of the orifice at the same time are produced through the specimens with wing cracks, and the heterogeneity coefficient affects the strike of the secondary cracks. Pre-ballast specimen with tensile failure in the late stage of the main and ballast stage, the tensile-shear combination is mainly destroyed, and the generation of secondary cracks is related to the shear failure. The cumulative energy of the acoustic emission and the acoustic emission increased slowly in the early stage; and rapidly in the later stage, the smaller the inclination angle of the pre-cast crack, the larger the heterogeneous coefficient, the greater the accumulated energy of the acoustic emission, and the stress time curves of the test pieces at different crack inclination angles and different mean values are all subjected to three stages. The existence of the porosity reduces the peak strength of the samples and affects the brittleness of the specimens. The results of the study provide some reference for further understanding the law of the pore-gap interaction.

uniaxial stress; pore-fracture action; acoustic emission; crack propagation; stress-strain curve; numerical simulation

TD31

A

10.3969/j.issn.1001-1986.2020.02.027

1001-1986(2020)02-0179-08

2019-05-20；

2019-11-18

长城钻探工程有限公司科研项目(GWDC2017B-01)

Science and Research Project of Engineering and Technology Research Institute of Great Wall Drilling Engineering Co. Ltd.(GWDC2017B-01)

郭修成，1986年生，男，四川广安人，工程师，从事钻井工程等相关研究工作. E-mail：guoxc.gwdc@cnpc.com.cn

郭修成. 单轴应力下的孔洞–裂隙扩展规律数值模拟[J]. 煤田地质与勘探，2020，48(2)：179–186.

GUO Xiucheng. Numerical simulation of propagation law of pore-fracture under uniaxial stress[J]. Coal Geology & Exploration，2020，48(2)：179–186.

(责任编辑 周建军)