基于HC温升曲线的T梁抗弯承载能力分析*

郭梓栋 李 红

(武汉理工大学交通学院 武汉 430063)

预应力混凝土连续T梁在实际工程中应用广泛，是我国高速公路、城市道路路网建设的主要桥型之一。但该结构的火灾研究有限，在该类桥型发生火灾后，养护单位和管养人员缺少一定的科学依据对其进行准确的评估及加固处理。因此，对预应力混凝土连续T梁进行桥梁火灾后的结构力学性能和特征研究具有一定意义。

1906年，美国某研究机构提出了钢筋混凝土结构的抗火性能试验方法，并建立了ASTME119温度上升曲线[1-3]，这项研究为以后学者研究钢筋混凝土结构的抗火性能奠定了基础。1965年，瑞典学者Ove Petterson第一次提出建筑结构抗火设计的理念，随后各国也陆续发布了自己的结构抗火设计规范，其中包括欧洲钢结构协会规范、澳大利亚AS4100规范和欧洲EC规范等[4]。时旭东等[5]将钢筋混凝土结构的温度场视为非线性瞬态热传递问题，在合理简化的前提下，推出了高温变形的一般规律，创建了混凝土温度-应力耦合的本构关系。吕彤光等[6]对建筑结构中常用的5种等级钢筋进行了试验，分析了在不同温度影响下钢筋的本构关系、短期徐变、强度等的变化规律。

目前，已有学者对T梁不同部位遭受火灾下桥梁的形变和应力规律进行了研究[7]，但是对于T梁在不同部位遭受火灾时的承载能力变化规律未见报道。本文拟通过ANSYS建立实体模型，研究T梁在不同部位遭受火灾时的温度变化，并计算分析不同火灾工况下T梁承载能力的变化规律。

1 有限元模型建立与温度场求解

本文以2×30 m连续T型梁桥为研究对象，研究不同火灾工况下T梁截面的抗弯承载能力衰减规律。建立分离式实体模型，混凝土单元选用SOLID70，该单元具有三维热传导能力，有8个节点，每个节点都具有单一自由度和温度，适用于三维、稳态和瞬态热分析；钢筋单元选用LINK33，LINK33是单轴元件，可以在节点之间传递热量，每个节点有单一的自由度、温度。将预应力钢筋与混凝土单元节点的温度进行耦合。

定义分析类型为瞬态分析，定义整体模型的初始温度、环境的初始温度、热辐射系数和对流换热系数等。定义HC温升曲线，即碳氢化合物温升曲线，通过ASEL命令选取不同的火灾工况，设置延火时间为120 min，求解温度场。

2 温度场分析

2.1 火灾工况设计

为研究预应力混凝土连续T梁的温度场分布情况，设计了多种火灾工况，其内容见表1。

表1 预应力混凝土连续T梁火灾工况(火灾部位：第一跨；受火长度：10 m；延火时间：120 min)

2.2 温度云分析

选取PC3工况作为典型工况进行温度场分析，研究预应力混凝土T梁在火灾作用下混凝土及预应力钢筋的温度分布情况。PC3工况下第一跨的跨中截面在延火60 min和延火120 min的温度云图见图1。

由图1可见，T梁在受火时，温度延受火面为层状分布，且呈U形，随着时间的增加，高温区域逐渐由受火面向内部发展。延火时间为60 min时，峰值温度为1 099.96 ℃；延火时间为120 min时，峰值温度为1 100 ℃，说明60 min时受火面温度已经接近最大值，随着时间的推移，温度不再增加，高温区域的范围会更加广泛。

预应力钢筋在PC3工况(T梁腹板和翼缘底部着火)下的温度云图见图2。可以明显地看出，最上层预应力钢束由于距离腹板底部较远，温度上升比下2层预应力钢束缓慢。延火时间为60 min时，下2层预应力钢束最高温度为504.027 ℃，最上层预应力钢束最高温度为466.94 ℃；延火时间为120 min时，3层预应力钢束最高温度均为550.52 ℃。

图2 PC3工况第一跨预应力钢筋受火温度云图

3 火灾下预应力T梁的抗弯承载能力分析

3.1 基本假定

1) 在高温状态下，混凝土计算的平截面假定、各向同性假定和小变形假定均未发生改变。

2) 不考虑预应力钢筋与混凝土之间的黏结滑移。

3) 不考虑受拉区混凝土的抗拉能力。

3.2 混凝土强度换算

混凝土材料在高温场中性能会下降，在温度场分析中，可以看出温度呈层状分布。根据虚拟层烧损深度的原理，每一层混凝土对截面强度都有贡献，每一层强度的总和即为混凝土截面的总强度。计算公式为

(1)

式中：σ为常温下混凝土强度；A为常温下混泥土有效面积；N为截面上划分的混凝土虚拟层数[7]；σi为第i层混凝土截面层相对应温度的材料强度；Ai为第i层混凝土截面层面积。

在T梁的跨中截面设置温度测点，并在ANSYS中获取该测点在不同时间段的温度。在T梁翼缘处选取6个测点，每个测点间距为3 cm；T梁腹板两侧选取8个测点，每个测点间距为3 cm；T梁腹板底部选取12个测点，每个测点间距3 cm。以PC1工况下T梁翼缘板烧损深度换算为例，根据式(1)计算翼缘板混凝土h=3，6，9，12，15 cm在不同延火时间的深度换算、烧损深度换算叠加值，见表2。

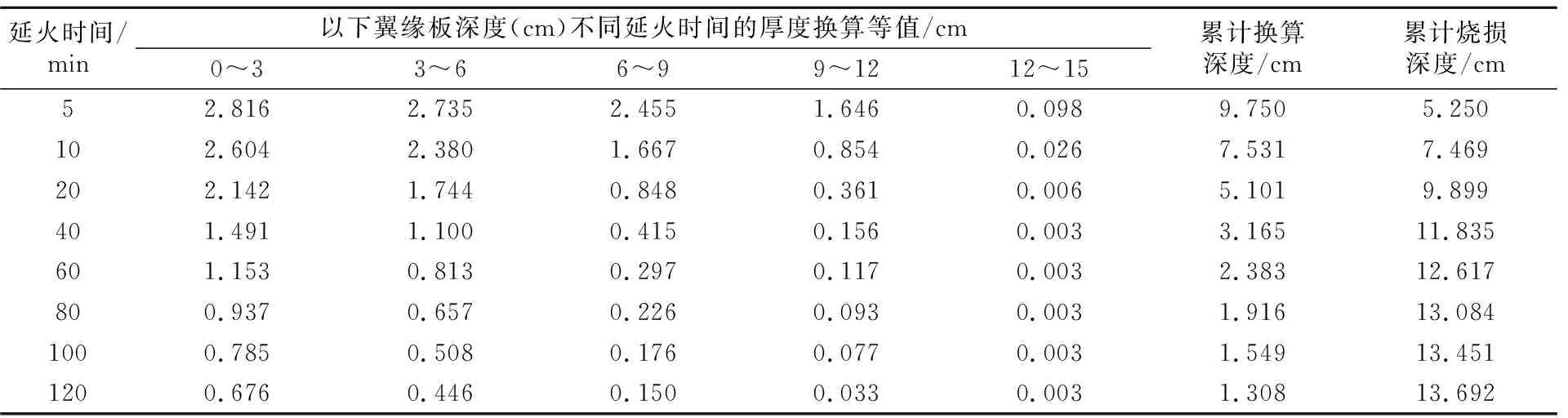
表2 混凝土换算深度累加值

由表2可知，翼缘板混凝土烧损严重，延火60 min时，烧损深度达到12.617 cm，延火120 min时，烧损深度增加至13.692 cm。远离受火面的混凝土烧损后强度高，换算烧损深度小。

3.3 预应力钢束强度折减

由温度场分析可知，预应力钢束的温度随延火时间的增加而增加，并且越靠近受火面，其温度越高，在跨中截面处，预应力钢筋温度达到峰值。按照欧洲EC3规范[4]提供所给的预应力钢束在不同温度下的强度折减系数，来计算在不同工况下跨中截面的钢束强度折减情况。

以PC1工况下的强度换算为例，强度换算表见表3。

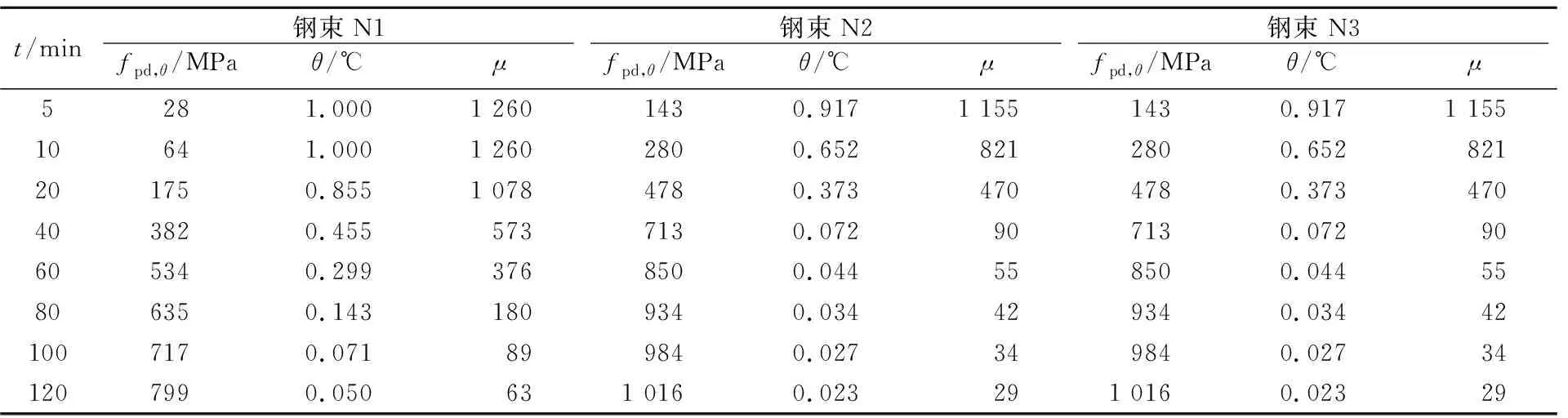
表3 PC1工况下预应力钢束的强度折减(跨中截面)

注：t为延火时间；θ为钢束在不同延火时间的温度；μ为钢束在高温下的屈服强度折减系数；fpd,θ为预应力钢束在高温下的折减强度。

由表3可知，N1钢束在延火60 min时的强度降低至376 MPa，延火120 min时，强度降低至63 MPa；N2和N3钢束在延火60 min时的强度降低至55 MPa，延火120 min时，强度降低至29 MPa。远离受火面的钢束强度折减较少。

3.4 预应力混凝土T梁正截面抗弯承载能力计算

本文在选用计算公式时，在满足3.1节基本假定的前提条件下，采用JTG D62-2014《公路钢筋混凝土及预应力混凝土桥涵设计规范》[8]中第五章规定的第一类T梁正截面抗弯承载能力计算公式，计算时，采用不同工况下的混凝土换算深度和预应力钢筋的强度折减值。根据工程实例和本文钢筋布置情况对公式进行修正如下。

(2)

fpd,tAp=fcdbtxt

(3)

h0=ht-at

(4)

式中：γ0为桥涵结构的重要性系数；Md为弯矩设计值；Mu,t为在不同延火时间下所选截面的抗弯承载能力；fcd为混凝土轴心抗压强度设计值；bt为不同延火时间下的T型腹板截面宽度；xt为不同延火时间下的混凝土受压区高度；h0为不同延火时间下的截面有效高度；ht为不同延火时间下的混凝土截面换算高度；at为预应力钢筋合力点到受拉区边缘的距离，这里取合力点以下的每层混凝土截面换算深度的叠加；fpd,t为不同延火时间下的预应力钢筋抗拉强度设计值；Ap为受拉区纵向预应力钢筋截面面积。

不同工况下跨中截面的计算结果见表4，其中：μ为正截面抗弯承载能力衰减系数，其表达式为

(5)

式中：Mu为常温下对应截面的正截面抗弯承载能力。

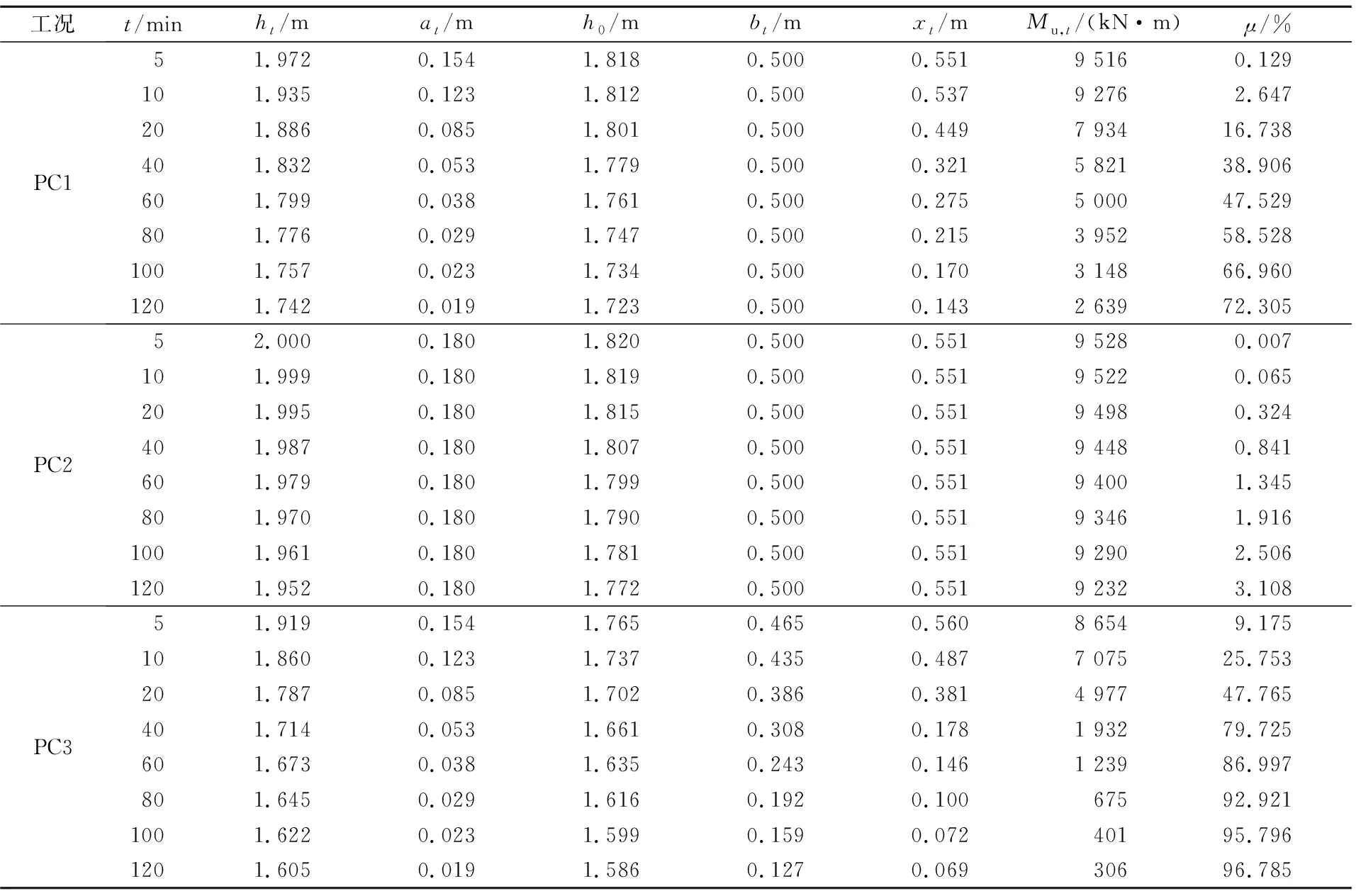
表4 不同工况下正截面抗弯承载能力计算(跨中截面)

3.5 火灾后基于正截面抗弯承载力的安全评判

采用JTG D60-2015《公路桥涵设计通用规范》[9]给出的作用偶然组合的效应设计值进行计算，荷载组合为

Sad=G1k+G2k+0.4Q1k+0.4Q2k

(6)

式中：Sad为承载能力极限状态下作用偶然组合的效应设计值；G1k为结构自重；G2k为二期恒载；Q1k为汽车荷载；Q2k为人群荷载。

按规范取值，计算得到跨中截面的荷载效应组合值为4 905 kN·m。将计算所得荷载效应组合值与火灾下的抗弯承载力进行对比，安全性能对比图见图3。

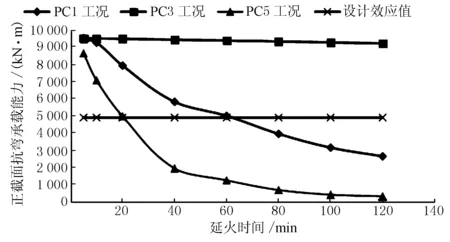
图3 安全性能对比图

由图3可知在桥面受火时，由于桥面铺装和防水层具有隔热作用，T梁的翼缘温变化较缓慢，抗弯承载力的衰减较小，预应力混凝土T梁的抗弯承载能力依然满足要求，并且此时的抗弯承载力远大于设计值，安全性较高；在腹板底部单面受火时，承载能力下降的速度较慢，在延火时间为1 h以内，安全性较好；在腹板和翼缘板多面受火时，承载能力剧烈下降，在延火时间为20 min时，抗弯承载能力已经不能满足设计要求，安全性差。

4 结语

1) 建立了有限元模型，研究了HC温升曲线下，T梁多面受火时的温度分布情况，研究表明混凝土截面的温度分布沿受火面呈层状分布，且呈U形。

2) 假定了本文计算的前提条件，基于虚拟层烧损深度换算原理，给出混凝土烧损深度的换算公式并进行计算；得到了在不同工况下预应力钢筋在高温下的强度折减。

3) 基于本文的温度场结果和计算模型，计算并分析T梁跨中截面在不同火灾工况下的抗弯承载力随延火时间的变化。结果表明，T梁在桥面受火时承载能力衰减程度低，承载力远大于设计值，满足要求；T梁腹板底部及多面受火时，承载能力衰减先迅速后缓慢，在一段时间后均不满足要求。